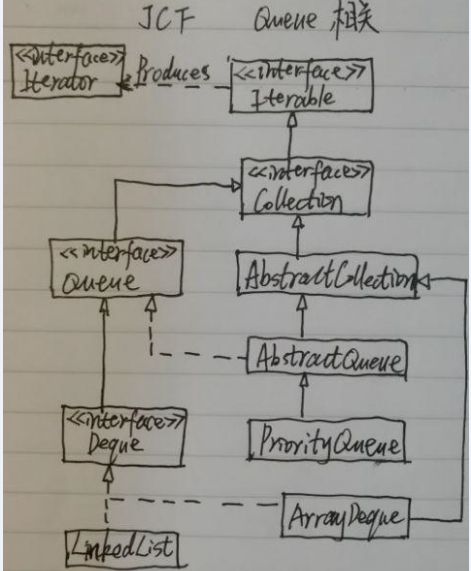
PriorityQueue:优先级队列;
在介绍该类之前,我们需要先了解一种数据结构——堆,在有些书上也直接称之为优先队列;
堆(Heap)是是具有下列性质的完全二叉树:每个结点的值都 >= 其左右子结点的值,称为最大堆(Max Heap,或称大顶堆);每个结点的值都 <= 其左右子结点的值,称为最小堆(Min Heap,或称小顶堆);
Note:上述定义摘自《大话数据结构》,其定义并不是很准确,堆有很多种,完全二叉树只是其一种实现方式,也是最常见的一种实现方式。在《数据结构与算法分析艺术中》有言:当堆这个词不加修饰地使用时一般指该数据结构的二叉堆实现方式。(也即这里所说的完全二叉树的实现方式)。
完全二叉树的最简单的实现方式是数组实现:
对于数组中任意位置i上的元素,其左儿子在位置2i上,右儿子在左儿子的右边,位置为2i+1,它的父结点位于i/2位置上。
Note1:上述假设数组第0个位置不存储堆元素(作为一个哨兵),第1个位置的元素为根结点;
如果第0个元素存储堆元素,那么左儿子应该为2i+1,右儿子为2(i+1),根结点为位置为0的元素;
PriorityQueue中的数组第0个位置存储堆元素。
综合堆的定义和完全二叉树的表示方式,可以用如下方式表示一个二叉堆:
arr[i] <= arr[2i],arr[i] <= arr[2i+1] (最小堆)
或者
arr[i] >= arr[2i],arr[i] >= arr[2i+1] (最大堆)
其中 1 <= i <= n / 2Note:同Note1
java的PriorityQueue的内部实现原理就是一个数组表示的最小堆,对于一个最小堆,其最重要的3个操作如下:
Insert:插入一个元素
DeleteMin:删除最小元素
BuildHeap:已知n个元素,构建一个堆关于上述3中操作,这里我做一些举例,为了形象的说明这些操作的步骤,贴上《数据结构与算法分析》这本树上的一些内容图片。
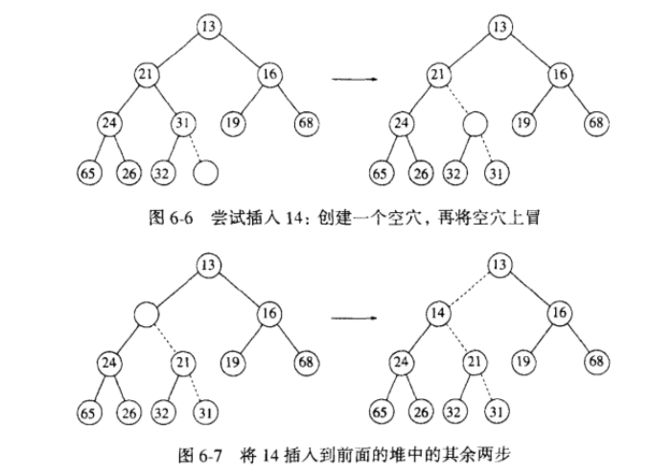
Insert:
插入一个新元素,先在这个堆的最后插入一个空穴,然后将这个元素与空穴的父结点进行比较,如果比父结点小,那么将用父结点的元素移动到这个空穴中,并将空穴上移;如果比父结点大,此时空穴的位置即为插入的元素应该在的位置,直接用插入的元素填到这个空穴即可。这个空穴上移的过程称之为上滤,对应于PriorityQueue总的siftup().
下图比较好地解释了这个过程。
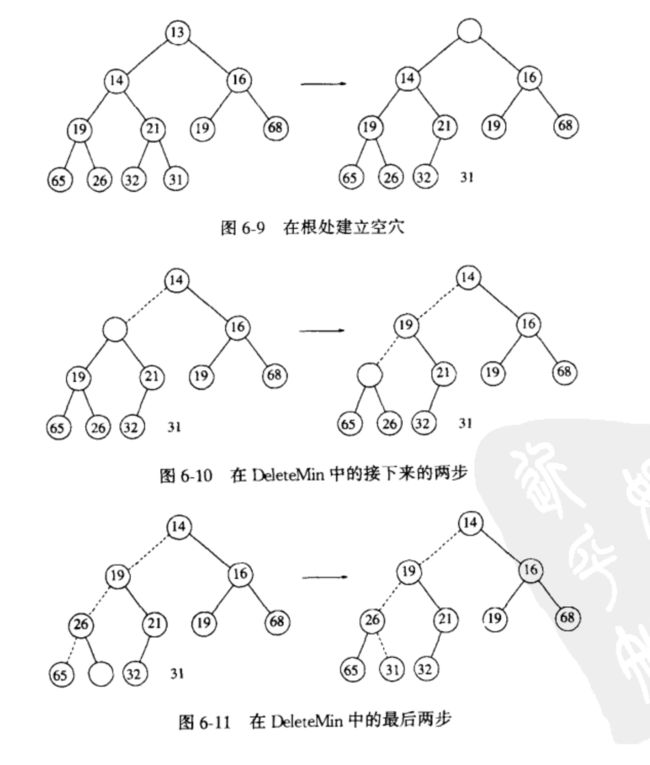
DeleteMin:
最小的元素,也就是根节点的额元素,直接取出。这是根这个位置形成一个空穴,最后一个元素因为堆的大小减1,需要移动其到新的位置。这是将其余根的较小的子节点进行比较,如果比子节点大,将较小的子节点移动到空穴中,并将空穴下移到这个较小的子节点处。如果比这个较小的子节点小,那么当前空穴即为该元素的最终位置。这个空穴下移的过程称为下滤,对应于PriorityQueue总的siftdown().
下图比较好地解释了这个过程。
BuildHeap:
BuildHeap有两种实现方式:
- 将所有的元素逐个Insert到堆中,因为插入一个元素的时间复杂度为O(logn),插入n个元素的时间复杂度为O(nlogn)
- 将所有元素赋值到堆中,在将这些元素从下往上逐步调成一个完整的堆,可以通过数学方法算出,这种实现方式的时间复杂度为O(n)
因为时间复杂地更低,通常使用第2种方式。
下图比较好地解释了这个过程。

关于堆的基础知识已经介绍完了,java的PriorityQueue的内部实现原理就是一个数组表示的最小堆,我们来看源码:
/**
* 一个基于堆数据结构的优先级队列;
* 优先级队列中的元素按照其自然序列排序或指定的Comparator对象进行排序,具体使用的排序方式取决于调用的构造方法;
* 不允许null元素;
* 如果不使用Comparator,那么元素本身必须实现Comparable接口的;
* 优先队列的头部元素为排序后的最小元素,如果最小元素有多个,可能是其中的任意一个;
* 自动扩容;
* 非线程安全;
* 入队和出队的时间复杂度为O(log(n));
* 删除指定元素removeAt(index)和查找指定元素的时间复杂度为O(n);
* iterator()返回的Iterator对象不保证对优先队列进行遍历的顺序(这个在源码注释中再细讲),推荐使用Arrays.sort(pq.toArray())}进行顺序遍历;
* @since 1.5
*/
public class PriorityQueue extends AbstractQueue implements java.io.Serializable {
private static final long serialVersionUID = -7720805057305804111L;
// 默认初始化大小:11
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// 极限大小
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
// 表示一个最小堆(或称优先队列);
// 节点queue[n]的两个子节点为queue[2*n]和queue[2*(n+1)];
// 根节点为queue[0],也就是排序出来的最小值;
// 本队列按照指定的comparator排序,如果comparator为null,按元素的自然顺序排序;
// 这里所谓的自然排序是指类型本身实现了Comparable接口;
private transient Object[] queue;
private int size = 0;
// 指定的comparator,如果为null,按元素的自然顺序排序;
private final Comparator comparator;
private transient int modCount = 0;
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityQueue(int initialCapacity) {
this(initialCapacity, null);
}
public PriorityQueue(int initialCapacity, Comparator comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity];
this.comparator = comparator;
}
@SuppressWarnings("unchecked")
public PriorityQueue(Collection c) {
if (c instanceof SortedSet) {
// SortedSet是排序好的,copy一份数据建堆即可
SortedSet ss = (SortedSet) c;
this.comparator = (Comparator) ss.comparator();
initElementsFromCollection(ss);
} else if (c instanceof PriorityQueue) {
// 既然是以指定的集合本身就是一个优先队列,那么就直接复制元素就行了,不用再调整成一个最小堆
PriorityQueue pq = (PriorityQueue) c;
this.comparator = (Comparator) pq.comparator();
initFromPriorityQueue(pq);
} else {
this.comparator = null;
// 堆的BuildHeap的完整流程,集合中的元素可能本身并没有排序好,除了复制元素之外,还要将所有的元素调整成一个最小堆
initFromCollection(c);
}
}
@SuppressWarnings("unchecked")
public PriorityQueue(PriorityQueue c) {
this.comparator = (Comparator) c.comparator();
initFromPriorityQueue(c);
}
@SuppressWarnings("unchecked")
public PriorityQueue(SortedSet c) {
this.comparator = (Comparator) c.comparator();
initElementsFromCollection(c);
}
private void initFromPriorityQueue(PriorityQueue c) {
if (c.getClass() == PriorityQueue.class) {
this.queue = c.toArray();
this.size = c.size();
} else {
initFromCollection(c);
}
}
// 将Collection中的元素全部克隆到队列中
private void initElementsFromCollection(Collection c) {
Object[] a = c.toArray();
// If c.toArray incorrectly doesn't return Object[], copy it.
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, a.length, Object[].class);
int len = a.length;
if (len == 1 || this.comparator != null)
for (int i = 0; i < len; i++)
if (a[i] == null)
throw new NullPointerException();
this.queue = a;
this.size = a.length;
}
// BuildHeap有两种实现方式:
// 1. 将所有的元素逐个Insert到堆中,因为插入一个元素的时间复杂度为O(logn),插入n个元素的时间复杂度为O(nlogn)
// 2. 将所有元素赋值到堆中,在将这些元素从下往上逐步调成一个完整的堆,可以通过数学方法算出,这种实现方式的时间复杂度为O(n)
// 该方法使用的是第2种实现方式
private void initFromCollection(Collection c) {
initElementsFromCollection(c);
// 将队列中的数据调整为一个优先队列(最小堆)
heapify();
}
// 扩容
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// 容量 < 64的时候,扩容后2倍 + 2(这里为什么+2,应该是考虑优先级初始化时的大小可能为1,这里+2,让容量很小时,增长速度更快)
// 否则扩容后1.5倍
int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2) : (oldCapacity >> 1));
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;
}
public boolean add(E e) {
return offer(e);
}
// 堆内添加指定元素,也就是堆的Insert操作
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);
size = i + 1;
// 原来元素个数为0
if (i == 0)
queue[0] = e;
else
// 添加了新元素,当前空的地方(空穴)就是当前堆的最后一个位置,待找到具体位置的元素为添加的这个元素
// 这个过程为上滤
siftUp(i, e);
return true;
}
// 直接返回根节点元素即可
public E peek() {
if (size == 0)
return null;
return (E) queue[0];
}
// 顺序查找,时间复杂度为O(n),通过equals()判断元素相等
private int indexOf(Object o) {
if (o != null) {
for (int i = 0; i < size; i++)
if (o.equals(queue[i]))
return i;
}
return -1;
}
// 删除指定元素,时间复杂度为O(n),通过equals()判断元素相等
public boolean remove(Object o) {
int i = indexOf(o);
if (i == -1)
return false;
else {
removeAt(i);
return true;
}
}
// 移除指定元素,时间复杂度为O(n),使用 == 来判断元素相等
boolean removeEq(Object o) {
for (int i = 0; i < size; i++) {
if (o == queue[i]) {
removeAt(i);
return true;
}
}
return false;
}
public boolean contains(Object o) {
return indexOf(o) != -1;
}
public Object[] toArray() {
return Arrays.copyOf(queue, size);
}
public T[] toArray(T[] a) {
if (a.length < size)
// Make a new array of a's runtime type, but my contents:
return (T[]) Arrays.copyOf(queue, size, a.getClass());
System.arraycopy(queue, 0, a, 0, size);
if (a.length > size)
a[size] = null;
return a;
}
public Iterator iterator() {
return new Itr();
}
private final class Itr implements Iterator {
private int cursor = 0;
private int lastRet = -1;
private E lastRetElt = null;
private int expectedModCount = modCount;
private ArrayDeque forgetMeNot = null;
public boolean hasNext() {
return cursor < size || (forgetMeNot != null && !forgetMeNot.isEmpty());
}
public E next() {
if (expectedModCount != modCount)
throw new ConcurrentModificationException();
if (cursor < size)
// 默认顺序遍历数组
return (E) queue[lastRet = cursor++];
if (forgetMeNot != null) {
// 顺序遍历数组到了最后,开始遍历之前未被遍历到的元素,也就是forgetMeNot双端队列中的元素
lastRet = -1;
lastRetElt = forgetMeNot.poll();
if (lastRetElt != null)
return lastRetElt;
}
throw new NoSuchElementException();
}
// 删除指定位置的元素,可能存在上滤的操作,导致之后需要遍历的元素被移动至之前已经遍历过的一个位置,
// 将这样的元素移至forgetMeNot双端队列中
public void remove() {
if (expectedModCount != modCount)
throw new ConcurrentModificationException();
if (lastRet != -1) {
// 还在顺序遍历数组的过程
E moved = PriorityQueue.this.removeAt(lastRet);
lastRet = -1;
// 在removeAt()中没有siftup操作,这里直接将cursor回退即可(之后没有遍历的被移动元素被移动到了这个位置)
if (moved == null)
cursor--;
else {
// 在removeAt()中有siftup操作,将这个未被遍历的元素移动到forgetMeNot双端队列中,
// 备后续数组遍历完成后,再遍历这个双端队列中的元素
if (forgetMeNot == null)
forgetMeNot = new ArrayDeque<>();
forgetMeNot.add(moved);
}
} else if (lastRetElt != null) {
// 顺序遍历数组已经完成了,接下来就是处理forgetMeNot双端队列中的元素了
PriorityQueue.this.removeEq(lastRetElt);
lastRetElt = null;
} else {
throw new IllegalStateException();
}
expectedModCount = modCount;
}
}
public int size() {
return size;
}
public void clear() {
modCount++;
for (int i = 0; i < size; i++)
queue[i] = null;
size = 0;
}
// 取出根节点的元素,将剩下的元素调整成堆
public E poll() {
if (size == 0)
return null;
int s = --size;
modCount++;
// 第0个元素就是根节点
E result = (E) queue[0];
E x = (E) queue[s];
// help GC
queue[s] = null;
if (s != 0)
// 因为取出一个元素,空穴位置为0,堆变小
// 待找到具体位置的元素为删除前的堆最后一个元素
// 这个过程为下滤
siftDown(0, x);
return result;
}
// 一般情况下,返回null,如果存在上滤操作,返回上滤的元素
private E removeAt(int i) {
assert i >= 0 && i < size;
modCount++;
int s = --size;
if (s == i) // removed last element
queue[i] = null;
else {
E moved = (E) queue[s];
queue[s] = null;
siftDown(i, moved);
// 这里为什么会有上滤,可以参考
// [In Java Priority Queue implementation remove at method, why it does a sift up after a sift down?]
// (https://stackoverflow.com/questions/38696556/in-java-priority-queue-implementation-remove-at-method-why-it-does-a-sift-up-af)
// 这里也是iterator()返回的Iterator对象不保证对优先队列进行遍历的顺序的原因
if (queue[i] == moved) {
siftUp(i, moved);
if (queue[i] != moved)
return moved;
}
}
return null;
}
// 上滤,k为当前空穴位置,x为待找到具体位置的元素
// sift:筛选;过滤
private void siftUp(int k, E x) {
// 按照设置的排序规则进行上滤
// 如果设置了comparator,以comparator为准
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
// 这个实现与siftUpUsingComparator其实一样
private void siftUpComparable(int k, E x) {
// 如果没有comparator,那么元素本身就要实现Comparable接口
Comparable key = (Comparable) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (key.compareTo((E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = key;
}
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
// 空穴的父结点位置
int parent = (k - 1) >>> 1;
Object e = queue[parent];
// x比空穴父结点大,当前空穴就是x的位置
if (comparator.compare(x, (E) e) >= 0)
break;
// x比该元素小,当前空穴被其父结点代替
queue[k] = e;
// 空穴上移
k = parent;
}
queue[k] = x;
}
// 下滤,k为当前空穴位置,x为待找到具体位置的元素
private void siftDown(int k, E x) {
// 按照设置的排序规则进行下滤(这个过程中空穴下移)
// 如果设置了comparator,以comparator为准
if (comparator != null)
siftDownUsingComparator(k, x);
else
siftDownComparable(k, x);
}
private void siftDownComparable(int k, E x) {
Comparable key = (Comparable) x;
int half = size >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = queue[child];
int right = child + 1;
if (right < size && ((Comparable) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
if (key.compareTo((E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = key;
}
private void siftDownUsingComparator(int k, E x) {
int half = size >>> 1;
while (k < half) {
// 左结点位置
int child = (k << 1) + 1;
Object c = queue[child];
// 右结点位置
int right = child + 1;
// 从左右两个子结点中选出一个较小的
if (right < size && comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
// 如果x比较小的元素更小,x的位置就为当前空穴位置
if (comparator.compare(x, (E) c) <= 0)
break;
// 这个较小的元素填到当前空穴位置
queue[k] = c;
// 空穴下移
k = child;
}
queue[k] = x;
}
// 已经有了数据,但是其中的数据是无序的,将其调整为堆,使用这种方式进行调整时间复杂度为O(n)
private void heapify() {
// 从高度为1的层开始,对每一个结点,将其本身和左右子堆调整为一个更大的堆(添加了当前结点)
for (int i = (size >>> 1) - 1; i >= 0; i--)
// 空穴位置为当前结点位置,待找到具体位置的元素为当前结点
siftDown(i, (E) queue[i]);
}
public Comparator comparator() {
return comparator;
}
private void writeObject(java.io.ObjectOutputStream s) throws java.io.IOException {
s.defaultWriteObject();
s.writeInt(Math.max(2, size + 1));
for (int i = 0; i < size; i++)
s.writeObject(queue[i]);
}
private void readObject(java.io.ObjectInputStream s) throws java.io.IOException, ClassNotFoundException {
s.defaultReadObject();
s.readInt();
queue = new Object[size];
for (int i = 0; i < size; i++)
queue[i] = s.readObject();
heapify();
}
}