很多人可能听过大名鼎鼎的SVM,这里介绍的正是SVM算法的基础——感知机,感知机是一种适用于二类线性分类问题的算法
原理
问题的输入与输出:
X = {$x_1,x_2,...,x_n$}
Y = {+1, -1}模型:
感知机的目的是找到一个可以正确分类数据的超平面S:$\omega\cdot x+b=0$, 其中$\omega$是超平面的法向量,b是截距,得到感知机模型 $f(x)=sign(\omega\cdot x+b)$,其中$\omega\cdot x+b>0$为正类,$\omega\cdot x+b<0$为负类策略:
接下来的问题就是如何找到最优模型,简单说就是定义损失函数并将损失函数最小化。损失函数需要是关于ω,b的连续可导函数,这里采用的正是误分类点离超平面的距离。
$\because$输入空间任意一点 $x_i$ 到超平面的距离为 $\frac{1}{||\omega||}|\omega \cdot x_i+b|$,
$\because$对于任意误分类的点: $-y_i(\omega \cdot x_i+b)>0$
$\therefore$点到超平面的距离可以表示为$-\frac {1}{||\omega||}y_i(\omega \cdot x_i+b)$
$\therefore$所有误分类的点到超平面的距离之和为:$\frac {1}{||\omega||}\sum_{x_i\in M}y_i(\omega\cdot x_i+b)$ ,其中M表示所有误分类的点的集合
$\therefore$不考虑$\frac {1}{||\omega||}$ , 损失函数可以写成 $L(\omega,b)=\sum_{x_i\in M}y_i(\omega\cdot x_i+b)$
感知机学习的策略就是寻找 $minL(\omega,b)=\sum_{x_i\in M}y_i(\omega\cdot x_i+b)$ 的 $\omega,b$算法:
直观的说,当有一个实例点被误分类时,实例点在分类超平面的错误一侧,调整 $\omega$ 和 b 的值,使得分离超平面向该点移动,以减少点到分类超平面的距离,直到越过改点使其正确分类
1.原始形式
$\because$$\nabla_\omega L(\omega,b)=-\sum_{x_i\in M}y_ix_i$ , $\nabla_bL(\omega,b)=-\sum_{x_i\in M}y_i$
$\therefore$对于$\eta \in(0,1]$, $\omega\leftarrow\omega+\eta y_ix_i$, $b\leftarrow b+\eta y_i$
得到感知机算法的原始形式:
(1)初始化$\omega_0 ,b_0$
(2)取数据集中的点 $(x_i,y_i)$
(3)如果 $-y_i(\omega\cdot x+b)\leq 0$ , 更新$\omega\leftarrow\omega+\eta y_ix_i$ , $b\leftarrow b+\eta y_i$
(4)重复(2) (3)直到数据集中的点都被正确分类
2.对偶形式
将 $\omega$ 记作$\hat\omega=(\omegaT,b)T$ , $x$ 记作 $\hat x=(xT,1)T$
Novikoff定理:
(1)存在$\gamma>0$,$y_i(\hat\omega_{opt}\cdot\hat x)=y_i(\omega_{opt}\cdot x+b)>\gamma$
(2)令$R=max_{1\leq i\leq N}||\hat x_i||$,在训练集上的误分类次数k满足$k\leq(\frac{R}{\gamma})^2$
证明:
(1)$\because$数据集是线性可分的,存在超平面可将数据集完全正确分开,取超平面为$\hat\omega_{opt}\cdot \hat x=\omega_{opt}\cdot x+b=0$,使得$||\hat\omega_{opt}||=1$$\because$ 有限的 $i=1,2,3,\cdots,N$,$y_i(\hat\omega_{opt}\cdot\hat x)=y_i(\omega_{opt}\cdot x+b)>0$
(2)$\hat\omega_{k-1}=(\omega_{k-1}T,b_{k-1})T$
$y_i(\hat\omega_{k-1}\cdot x_i)=y_i(\omega_{k-1}\cdot x_i+b_{k-1})\leq0$
$\omega_k \leftarrow\omega_{k-1}+\eta y_ix_i$
$\hat\omega_k=\hat\omega_{k-1}+\eta y_i\hat x_i$
$\hat\omega_{opt}\cdot\hat\omega_kamp;=\hat\omega_{opt}\cdot(\hat\omega_{k-1}+\eta y_ix_i)=\hat\omega_{opt}\cdot\hat\omega_{k-1}+\eta y_i\hat\omega_{opt}x_i\geq\hat\omega_{opt}\cdot\hat\omega_{k-1}+\eta\gamma\geq\hat\omega_{opt}\cdot\hat\omega_{k-2}+2\eta\gamma\geq\cdots\geq k\eta\gamma$
$||\hat\omega_k||2=||\hat\omega_{k-1}||2+2\eta y_i\hat\omega_{k-1}\cdot\hat x_i+\eta^2||\hat x_i||2\leq||\hat\omega_{k-1}||2+\eta^2||\hat x_i||2\leq||\hat\omega_{k-1}||2+\eta2R2\leq||\hat\omega_{k-2}||2+2\eta2R^2\leq\cdots\leq k\eta2R2$
$k\eta\gamma\leq\hat\omega_k\cdot\hat\omega_{opt}\leq||\hat\omega_k|| ||\hat\omega_{opt}||\leq\sqrt{k}\eta R$
$k2\gamma2\leq kR^2$
$k\leq(\frac{R}{\gamma})^2$
证明误分类的次数k是有上界的
令$\alpha_i=n_i\eta$ , 设 $\omega,b$ 经过 $n$ 次更新,$\omega,b$ 每次的增量可表示为$\alpha_iy_ix_i,\alpha_iy_i$
$\omega=\sum_{i=1}{N}\alpha_iy_ix_i,b=\sum_{i=1}{N}\alpha_iy_i$
得到感知机算法的原始形式:
(1)初始化$\alpha_0 ,b_0$
(2)取数据集中的点 $(x_i,y_i)$
(3)如果 $-y_i(\sum_{j=1}^{N}\alpha_jy_ix_j\cdot x_i+b)\leq 0$ , 更新$\alpha\leftarrow\alpha+\eta$ , $b\leftarrow b+\eta y_i$
(4)重复(2) (3)直到数据集中的点都被正确分类
实现
-
Python代码
import numpy as np import matplotlib matplotlib.use('TkAgg') from matplotlib import pyplot as plt # 载入数据 def load_data_set(file_name): fr = open(file_name) data_set = [] label = [] for line in fr.readlines(): line_data = line.strip().split('\t') data_set.append([float(line_data[0]), float(line_data[1])]) label.append(float(line_data[2])) data_mat = np.mat(data_set) data_mat_new = np.insert(data_mat, 2, values=1, axis=1) return data_mat_new, label # 感知机分类学习 def precep_classify(data_mat, label_mat, eta=1): omega = np.mat(np.zeros(3)) m = np.shape(data_mat)[0] error_data = True while error_data: error_data = False for i in range(m): judge = label_mat[i] * (np.dot(omega, data_mat[i].T)) if judge <= 0: error_data = True omega = omega + np.dot(label_mat[i], data_mat[i]) return omega # 测试 def precep_test(test_data_mat, test_label_mat, omega): m = np.shape(test_data_mat)[0] error = 0.0 for i in range(m): classify_num = np.dot(test_data_mat[i], omega.T) if classify_num > 0: class_ = 1 else: class_ = -1 if class_ != test_label_mat[i]: error += 1 print error/m # 画图 def plot(data_mat, label_mat, omega): fig = plt.figure() ax = fig.add_subplot(111) X = data_mat[:, 0] Y = data_mat[:, 1] for i in range(len(label_mat)): if label_mat[i] > 0: ax.scatter(X[i].tolist(), Y[i].tolist(), color='red') else: ax.scatter(X[i].tolist(), Y[i].tolist(), color='green') o1 = omega[0, 0] o2 = omega[0, 1] o3 = omega[0, 2] x = np.linspace(3, 6, 50) y = (-o1 * x - o3) / o2 ax.plot(x, y) plt.show() # 主函数 def preceptron_main(): file_name = 'testSet.txt' # 载入数据文件,得到输入矩阵和标记列表 data_mat, label_mat = load_data_set(file_name) # 分类学习得到参数 omega = precep_classify(data_mat[:80], label_mat[:80]) # 用部分数据测试 precep_test(data_mat[80:], label_mat[80:], omega) plot(data_mat, label_mat, omega) if __name__ == "__main__": -
实验数据
3.542485 1.977398 -1 3.018896 2.556416 -1 7.551510 -1.580030 1 2.114999 -0.004466 -1 8.127113 1.274372 1 7.108772 -0.986906 1 8.610639 2.046708 1 2.326297 0.265213 -1 3.634009 1.730537 -1 0.341367 -0.894998 -1 3.125951 0.293251 -1 2.123252 -0.783563 -1 0.887835 -2.797792 -1 7.139979 -2.329896 1 1.696414 -1.212496 -1 8.117032 0.623493 1 8.497162 -0.266649 1 4.658191 3.507396 -1 8.197181 1.545132 1 1.208047 0.213100 -1 1.928486 -0.321870 -1 2.175808 -0.014527 -1 7.886608 0.461755 1 3.223038 -0.552392 -1 3.628502 2.190585 -1 7.407860 -0.121961 1 7.286357 0.251077 1 2.301095 -0.533988 -1 -0.232542 -0.547690 -1 3.457096 -0.082216 -1 3.023938 -0.057392 -1 8.015003 0.885325 1 8.991748 0.923154 1 7.916831 -1.781735 1 7.616862 -0.217958 1 2.450939 0.744967 -1 7.270337 -2.507834 1 1.749721 -0.961902 -1 1.803111 -0.176349 -1 8.804461 3.044301 1 1.231257 -0.568573 -1 2.074915 1.410550 -1 -0.743036 -1.736103 -1 3.536555 3.964960 -1 8.410143 0.025606 1 7.382988 -0.478764 1 6.960661 -0.245353 1 8.234460 0.701868 1 8.168618 -0.903835 1 1.534187 -0.622492 -1 9.229518 2.066088 1 7.886242 0.191813 1 2.893743 -1.643468 -1 1.870457 -1.040420 -1 5.286862 -2.358286 1 6.080573 0.418886 1 2.544314 1.714165 -1 6.016004 -3.753712 1 0.926310 -0.564359 -1 0.870296 -0.109952 -1 2.369345 1.375695 -1 1.363782 -0.254082 -1 7.279460 -0.189572 1 1.896005 0.515080 -1 8.102154 -0.603875 1 2.529893 0.662657 -1 1.963874 -0.365233 -1 8.132048 0.785914 1 8.245938 0.372366 1 6.543888 0.433164 1 -0.236713 -5.766721 -1 8.112593 0.295839 1 9.803425 1.495167 1 1.497407 -0.552916 -1 1.336267 -1.632889 -1 9.205805 -0.586480 1 1.966279 -1.840439 -1 8.398012 1.584918 1 7.239953 -1.764292 1 7.556201 0.241185 1 9.015509 0.345019 1 8.266085 -0.230977 1 8.545620 2.788799 1 9.295969 1.346332 1 2.404234 0.570278 -1 2.037772 0.021919 -1 1.727631 -0.453143 -1 1.979395 -0.050773 -1 8.092288 -1.372433 1 1.667645 0.239204 -1 9.854303 1.365116 1 7.921057 -1.327587 1 8.500757 1.492372 1 1.339746 -0.291183 -1 3.107511 0.758367 -1 2.609525 0.902979 -1 3.263585 1.367898 -1 2.912122 -0.202359 -1 1.731786 0.589096 -1 2.387003 1.573131 -1 -
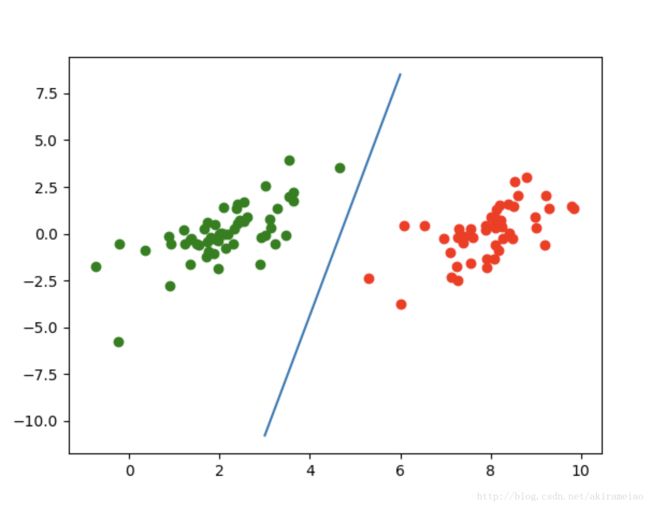
结果