这一篇首先会说说前面剩余的一点知识2-3树,然后简单说说B树,不写代码,只是简单看看原理吧!
为什么要说一下2-3树呢?了解2-3树之后能更快的了解B树;
1.简单看看2-3树
其实我们学过了前面的2-3-4树之后,再看2-3树就太容易了,2-3树中任意一个节点最多只有三个子节点,而且节点中只有两个空位置可以存数据;除了分裂,其他的都和2-3-4树一样的,就不多说了,下面我们就随意看看节点分裂吧!
首先要区分2-3-4树和2-3树分裂的的不同,对于2-3-4树来说是插入数据之前首先会把满的叶节点分裂,把三个数据分配完了之后再插入数据到节点中;而对于2-3树来说,是在插入期间,什么是插入期间呢?看看下图:
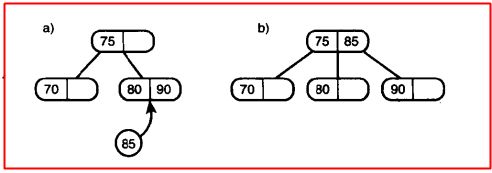
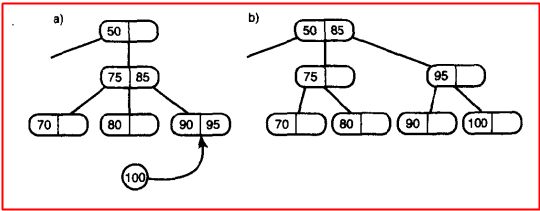
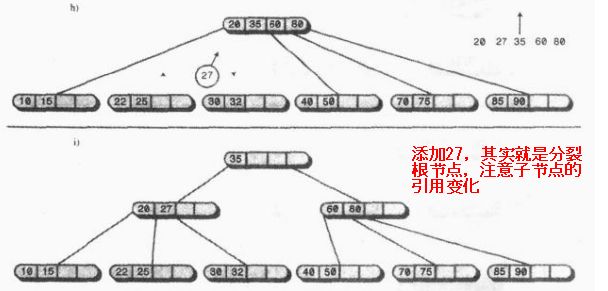
上图中的操作的目的就是向2-3树中插入85,插入的时候会判断该叶节点是不是满的,假如是满的 ,首先就80、90、85进行从小到大排列 为80、85、90,然后80不动,中间的数据放进父节点中,最后将90放入新创建的节点当中,就ok了;这里假如85在进入父节点的时候发现父节点满了,那么父节点就会分裂,这里跟2-3-4树差不多,重复上述步骤,左边数据不动,将中间值放入父节点,右边数据放入新建节点;说起来很绕,请看下图:
其实没什么新的东西,弄懂了2-3-4树,再看2-3树几分钟就差不多了,这里也就是随意看看,有兴趣的可以用代码实现一下,这里就是注意一下2-3树和2-3-4树分裂过程的不同就可以了;
2.硬盘存储数据
我们前面说的所有数据结构都是存在于内存中的,当电脑一关机内存就会全部释放,所有的数据结构都会消失;但是有没有想过硬盘中是怎么存数据的啊?
于是就有了B树,属于一种多叉树,在外部存储器存数据的时候起很大的作用,外部存储暂时就理解为硬盘即可!话说数据为什么要存到硬盘中呢?最大的有点就是硬盘便宜,而且硬盘空间比内存大得多,可以存很多很多的数据,而且硬盘最大的优点就是可以持久化,就是电脑即使关机了,数据还是存在硬盘中不会消失;
但是存在硬盘中有个很大的问题,就是从硬盘中读取数据的时候太慢太慢了,而从内存中读取数据的速度大概比硬盘读取快几万倍,相差一个数量级;其实对于cpu的运算速度来说从内存中读数据还是太慢了,于是就有了缓存,后面有机会再说......
虽然每年硬盘技术都在提高,但是内存技术提高的更快,可以想象内存和硬盘的速度只会越来越大!
2.1找到硬盘中数据的正确位置
假设我们要存一个城市的电话记录,大概50万条数据,每条数据512个字节,那么总共应该是50万x512=2亿5千6百万 字节,差不多就是256M,这个肯定不能存在内存中,要想办法把这256M的数据存到硬盘中还要保证我们从硬盘中查找,插入和删除指定记录的速度要足够快才行,不然用户体验太差了。。。
我们知道计算机想要读取硬盘中的数据是通过驱动(其实就是磁盘驱动器)去对硬盘进行操作,硬盘内部如下图所示,其实最终就是通过磁头对盘片进行操作,但是怎么操作呢?我们可以把盘片看作打靶的那个靶子一样有很多个圈,磁头首先要找到目标数据所在的圈(也叫做磁道)需要几毫秒,然后盘片需要旋转一下磁头才能在当前磁道中找到正确的位置(平均下来是要旋转半圈)需要几毫秒,找到正确的位置后,最后就是实际的读写操作了,差不多也需要几毫秒;假设硬盘这里的所有操作共需要10毫秒(10-3),而假如从内存中访问正确的数据则只需要几微秒(10-9),可以看到速度相差了好多好多倍;
那肯定有人要问了,既然内存这么快那干嘛不直接用内存条当硬盘来用呢?emmm....最主要的原因就是内存条很贵啊,你可以去淘宝或者京东查查几个G的内存条多少RMB,至少好几百,我们电脑存储量至少也要五六百个G吧,于是你买内存条就可以破产了;但是硬盘的话1T也就一两百块,价格才是最主要的。
2.2.读取数据块
磁头在硬盘的盘片中找到数据的正确位置了之后,难道要一条一条数据慢慢读么?当然不会用这么愚蠢的方法,我们可以把盘片中的数据分成一块一块的,需要的时候直接读取一块数据到内存中的缓存区,通常块的大小和操作系统和磁盘驱动器的容量相关,而且必须是2的倍数,假设这里我们把块的大小设置为8192字节(213),那么上面那两亿多个字节的数据就变成31250块;
块分完之后,假设我们要读取100字节的数据,那么磁盘驱动器首先直接读取一块数据,然后将这块数据前100字节留下其他的都扔了;假如是读取8292字节,那么就会读取两块数据,然后将第二块数据留下100字节就将第二块数据其他的都扔了;
顺便一说,上面说了一条数据512字节,一块数据是8192字节,可以知道一块数据其实就保存有16条记录,所以我们一次读取16条数据效率是最高的,不需要对数据进行丢弃操作;
2.3.硬盘中数据有序
我们存到硬盘中的数据,可以是有序和无序的;
假如硬盘中的数据是无序的,那么插入肯定是很快的,但是查询就比较坑了,因为硬盘中这么多数据要慢慢的进行遍历,那就只能慢慢等等了。。。
假如硬盘中的数据是有序排列的,那么我们去查找一条记录的时候就会很快,可以用二分法查找,到底有多快呢?假如你要从50万条数据中查找某条数据,最多需要查找19次,如果一次10微秒,那总共190微秒,比我们眨一下眼睛的时间还短;
二分法其实很容易的一个东西,举个例子一个数组中有顺序的数据0、1、2、3、4、5、6、7、8、9、10,我们要查找9所在的位置!假如我们用遍历那就需要10次;如果用二分法,首先9和中间的5比较,比5大,那就再和右半部分中间的8比较,比8大,继续在右边查找,可以找到9,只需要三次操作,数据量越大二分法的效果越明显;但是二分法也有缺陷就是必须要让数据有序,这就导致插入(或删除)的时候比较坑爹,就类似有序数组的插入,插入一个数据之后就要将这个数据后面的所有都往后移动一个位置,而且数据越多插入的效率越糟糕;
回到硬盘中数据的存储,假如我们将硬盘中的数据弄成有序的,分块完了之后(后面操作是以块为单位),查找可以用二分查找先找到某块数据,读取到磁盘驱动器的缓存中,然后里面就16条数据很快就可以找到;但是插入数据的话平均要移动一半的块,每移动一个块都需要一次硬盘的读写操作(就是都要经过2.1到2.2这个步骤然后把数据写入硬盘,贼坑!),下面就随意说说一次读写到底是怎么做的;
假如我们现在要插入一条记录A,第一步:首先会经过2.1和2.2读取一块数据并存在缓存中,将这块数据最后一条记录保存下来,然后判断记录A可以放在这块数据的哪里,适当移动这块数据中记录的位置并插入数据A,然后就把缓存区中的这块数据写入磁盘中;第二步:读取下一块数据,也是保存这块数据的最后一条记录,将这块数据中的记录都往后移动一个空位置,让上一块数据中保存的最后的一条记录插入到这块的最开始的位置,然后将本块数据写入磁盘;这个第二步会一直重复,直到将所有记录都重新写入。。。
我们上面数据分块是31250块,假如每次读写都要10毫秒,那么我们插入一条记录差不多需要5分钟,真是足够坑爹!
3.简单看看B树
根据上面我们可以知道数据存到硬盘中是分为两种情况的,但是两种情况各有优缺点,那有没有汲二者优点的存储方式呢?聪明的大佬们早就想出来了,这就像数组和链表的关系,最终我们引入了树的概念完美解决了数组和链表的缺陷,类似的现在我们在硬盘中也要引入一种树来解决,这种树就是B树;
B树是一种多叉树,也有人称为B-树,其实就是一种树!有点类似2-3-4树,只是B树每个节点都有很多个节点,那到底可以是多少个呢?我们慢慢看,补充一点,前面我们学习过的2-3树和2-3-4树都只是B树的两种特殊情况,如果对这两种树不熟悉的一定要先去看看;
根据前面的2-3-4树可以知道一个非叶节点的子节点数目 = 节点数据项+1,在B树中也是这样;还有,既然都说了2-3树和2-3-4树都只是B树的特殊情况,那就可以猜到B树的节点中的数据估计有很多个,我们该怎么选取节点才是最高效的呢?还记得前面说的分块吗,我们这里就是将一块数据作为一个节点;
我们再回顾一下上面说的城市的电话记录的例子,总共有2亿5千6百万字节,一条记录512字节,根据每一块数据8192字节(16条记录)进行分块,可以分为31250块,换句话说每块数据中存有16条数据,这就有点意思了,我们把每16条记录看作B树的一个节点的数据项,那么就应该有17个子节点才对;我们还知道每一个节点要保存子节点的引用,怎么做比较好呢?比较奢侈的做法是:让每个节点只保存15条记录,还有一条记录大小的空间用于存放子节点和父节点的引用吧!此时只有16个子节点;但是比较高效的做法是:一个节点中最好存偶数个数据,然后适当缩小每条记录的大小为507个字节,那么每一块中16条数据会占用8112字节,还剩下80字节,我们有17个子节点,每个子节点引用时int类型(一个int数据占4个字节)的数据,17x4=68 < 80,说明节点空间中即使保存子节点引用还是够用,下图所示:
下面我们简单说说B树的一些基本操作,不用代码来表示的,了解原理即可;
3.1 查找
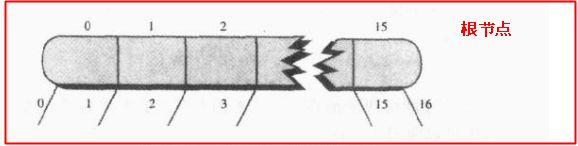
这个查找的操作和2-3-4树差不多,就是子节点多了很多而已,很容易!首先将根节点数据读到内存中,然后根据搜索算法对这个节点进行搜索,从0开始,其实就是比较在哪个范围下,然后继续到对应的子节点那里去找。。。重复这个步骤就能找到目的数据;
3.2 插入
插入这个操作就跟2-3树差不多了,为什么不用2-3-4树那样的插入方式呢?因为我们可以知道2-3-4树中的节点很多都是没有放满的,有很多节点只存了一个数据,有太多空位置,假如B树用这样的方式硬盘中会很浪费空间,而用类似2-3树这种方式利用率就比较高,我们可以看看B树中是怎么分裂的;
· 在插入数据的时候,假设该节点已经满了,我们还要向其中插入一个数据下图所示;
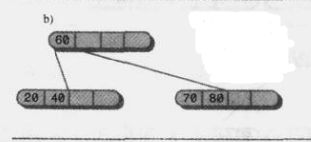
我们将70和节点中的数据进行从小到大排列,然后以中间数据60为界限,左边的数据不动,中间数据60放入父节点(根节点比较特殊,要新建一个父节点),右边的数据放入新建的节点:
继续插入18、30、15,过程如下,比较类似2-3树的分裂,没什么特别不好理解的,只是子节点比较多而已
最后看一个比较复杂的节点分裂,其实跟前面差不多。。。
可以简单看到B树中,除了根节点之外,其他的节点最低也会用一半的空间,利用率最低也是50%,这就已经很可以了;
4.B树效率
B树的效率如何呢?空间利用率还行,我们还是以最开始的那个城市电话记录为例子简单说说,总共有50万条记录以B树的形式存在硬盘中,每个节点至少也是半满,我们就以每个节点装满一半数据计算,可以算出树的高度大概为6,每个节点有8条记录(对应9个子节点);
至于到底怎么计算的,感觉没什么好说的,B树节点存数据的大小(或者说的块数据)是一定的,跟操作系统等因素有关,我们这里为16,每个节点存一半就是存8条数据,拥有9个子节点,是在不行用计算器算一下树的高度最低要为6才能存满50万数据,虽然我是对于这种计算的东西没多大兴趣。。。
由于树只有6层,那么我们查找任意一条数据也就需要6次比较而已,假设每次为10毫秒,那么最多就花费60毫秒,6/100秒;你想想从50万条数据中任意查找一条记录最多是6/100秒,这个效率已经很ok了,虽然查找效率已经很不错了,但是插入和删除操作才能显示出B树的最大优越性;
就比如说插入,假如插入数据到叶节点中,该叶节点没有满,那就不需要进行分裂,也就需要对硬盘7次操作,前六次是比较使得找到正确节点,第7次就是读取叶节点数据到缓存,插入数据然后写入硬盘;假如插入数据之后叶节点要进行分裂的话,找到叶节点、移动节点中的数据和创建新的节点等操作合在一起也就需要对硬盘的12步操作,这效率很厉害了,不能再多说了,这篇已经足够长了。。。
5.总结
B树其实也就这样吧,可能是没有仔细实现B树代码,但是感觉还行,最复杂的还是分裂这里,不过也就和2-3-4树差不了多少!
其实B树有很多种,我们常说的B树和B-树是一样的,还有B+树、B*树;其中B+树是对B-树的一个改进(多应用于操作系统索引和数据库索引),B*树又是对B+树的一个改进,了解了B-树之后再看后面这两种树很容易的,无非是增加几个指针,提高了节点利用率什么的,后面有时间再说吧!话说还有个R树,emmm....需要的时候再去看吧!