LCA问题

前言

我们的LCA是谁呢...

---

正文

LCA（Least Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。 ———摘自百度百科

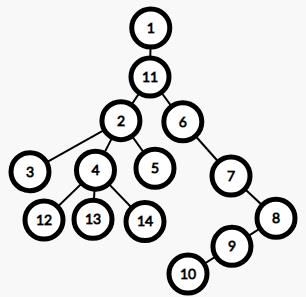
什么意思呢？上图

如你所见，这就是一棵超级难看的树了！

在这棵树中，\(3,4\)的LCA就是\(2\)，\(8,7\)的LCA就是\(7\)。

了解了LCA的概念之后，就要来思考怎么来求了。

在初学OI之时，我就已经见过LCA的板子题了，但是它的点数只有不到1k，所以我们考虑使用暴力解法，思路如下：

对于第一个点，可以一直递归的访问父亲结点直到根结点，用一个\(set\)来记录第一个点到根节点路径上的点。然后对于第二个点，也递归的访问父亲结点，遇到的第一个在\(set\)中出现过的点就是他们的公共祖先。

---

怎么样，简单吗？

如果点数与边数的范围都到了50W，还能用暴力解法进行解决吗？显然不行。暴力解法的时间复杂度过高，达到了\(O(n^2)\)，每次进行的查询太花费时间，怎么办？

回想一下暴力算法的步骤，跳跃深度较低的点到根节点并记录，跳跃深度较高的点并查询。这其中跳跃时的步长都是1，所以花费的时间过多。我们可以从此处着手进行优化。

倍增算法应运而生。

这又是一个跟\(2\)脱不了干系的算法，所谓倍增，就是要以2的倍数进行操作。即每次跳动的步长都以2的倍数来增大。即每次的步长为：\(1,2,4,8,16,32,...\)。

这样做又会出现一个问题。假如我需要跳动的步长为5，我会选择先跳1，再跳2，但是4又高了，需要退回2步。这样出现的“反悔”的跳法是极其浪费时间和难以实现的。所以我们再对倍增进行一些优化吧。

这次的优化，让跳跃的步长从大往下排列，即：\(...,32,16,8,4,2,1\)。这样的话，选择了一个数，剩下的部分也可以用同样的原理进行拆分，不会出现选多了的情况（只要选择的这个数不大于剩下的步数）

以二进制再形象地说一次吧。

\((5)_2=101\)

所以从低位开始的话，到第二位的时候是难以判断是否需要取的，因为1+2<5，看上去是可行的。但如果从高位开始，第二位的取舍就很清晰了，因为4+2>5，所以不选。

---

经过这样的优化，跳跃的次数被大大的减少了，时间复杂度可以降为\(O(nlogn)\)。

接下来就是代码实现的问题。

想要实现这个算法，首先我们要记录各个点的深度和他们\(2^i\)级的的祖先，用数组\(dep\)表示每个节点的深度，\(fa[i][j]\)表示节点\(i\)的\(2^j\)级祖先。

void dfs(int now,int last)
{
    dep[now]=dep[last]+1;
    fa[now][0]=last;
    for(int i=1;(1<

然后就是找LCA。

每次跳跃步长的起始指数用\(log2(n)\)，可以提前处理一下。

for(int i=1;i<=n;i++)
    p[i]=p[i-1]+(1<

接下来就是倍增LCA了，我们先把两个点提到同一高度，再统一开始跳。

但我们在跳的时候不能直接跳到它们的LCA，因为这可能会误判。找到的虽然是公共祖先，但不一定最近。

所以我们只跳到LCA的下面一层，再输出它们的父亲就可以了。

int lca(int x,int y)
{
    if(dep[x]dep[y]){x=fa[x][p[dep[x]-dep[y]]-1];}
    if(x==y)return x;
    for(int k=p[dep[x]];k>=0;k--)
        if(fa[x][k]!=fa[y][k])
            x=fa[x][k],y=fa[y][k];
    return fa[x][0];
}

ov.

---

完整代码

#include
using namespace std;
int read()
{
   int x=0,f=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){
       if(ch=='-')
           f=-1;
       ch=getchar();
   }
   while(ch>='0'&&ch<='9'){
       x=(x<<1)+(x<<3)+(ch^48);
       ch=getchar();
   }
   return x*f;
}
vector g[500010];
int dep[500010],fa[500010][25],head[500010],tot,p[500010];
struct node{int t,next;}e[500010<<1];
void add(int u,int v){e[++tot]=(node){v,head[u]},head[u]=tot;}
void dfs(int now,int last)
{
    dep[now]=dep[last]+1;
    fa[now][0]=last;
    for(int i=1;(1<dep[y]){x=fa[x][p[dep[x]-dep[y]]-1];}
    if(x==y)return x;
    for(int k=p[dep[x]];k>=0;k--)
        if(fa[x][k]!=fa[y][k])
            x=fa[x][k],y=fa[y][k];
    return fa[x][0];
}
int main()
{
    int n,m,s=1/*根节点*/,x,y;
    cin>>n>>m;
    for(int i=1;i