AVL树背景
在计算机科学中,AVL树是最先发明的自平衡二叉搜索树(BBST)。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis,他们在 1962 年的论文 "An algorithm for the organization of information" 中发表了它。
BBST 核心技巧
1. 满足适度平衡标准
2. 重平衡操作的技巧与算法
以 AVL树 为例,如何实现上述两条核心
AVL 树定义 :
1. 首先满足 BST 性质
2. 或者为空树,或者满足以下性质
- 任意节点的左右子树高度差的绝对值不大于1
- 其左右子树又都满足 AVL树
为此,引入 平衡因子 balFactor() : 左子树的高度减去右子树的高度
- balFactor(V) = height( LC(V) ) - height( RC(V) ). 即V的左子树高度-右子树高度
则 AVL 满足 : -1<= balFactor(V) <=1 (取值只有-1 , 0 ,1)
注:AVL满足适度平衡标准,有 height(AVL) = O( log n)
AVL相关接口
BinTree 中定义的 节点高度
#define NodeHeight(p) ((p) ? p->height : -1) //节点高度,约定空树的节点高度约定为 -1
AVL 接口
1. 理想平衡,左右子树高度相等
#define Balanced(x) \
(NodeHeight(x->lchild) == NodeHeight(x->rchild))
2. 平衡因子
#define BalFator(x) \
(NodeHeight(x->lchild) - NodeHeight(x->rchild)
3. AVL 平衡条件 BalFactor(x)在 [-1,1] 之间
#define AVLBalanced(x) \
( (-2 < BalFactor(x) ) && ( BalFactor(x) < 2 )
4. AVL 查找 Search() ... 可直接沿用 BST 的接口 <详见BST>
5. 需要重写的只有引起 AVL 结构变化的动态操作
5.1 插入操作
BinNodePosi insert(const T &);
5.2 删除操作
bool remove(const T &);
下面主要介绍 AVL 树的插入和删除操作
失衡与重平衡
[注] insert操作 相比 remove操作 的重平衡简单一点
1. AVL 插入节点操作
一个重要的结论 : AVL树 插入节点x,同时可有
多个失衡节点,从节点x 向上追溯其祖先,找到第一个失衡点(也称为最低失衡点),对最低失衡点进行"对应"的复衡操作(等价变换),子树的高度必然恢复,更高祖先也必复衡,全树也就恢复平衡。[注]
最低失衡点概念总结
首先引入最小不平衡子树: 插入节点导致失衡后,距离插入节点最近的,且平衡因子的绝对值大于 1 的节点为根的子树。
这个节点就称之为最低失衡点
对最小不平衡子树进行复衡操作,使子树恢复平衡,全树也会进而平衡。
- 上图 insert(M) 操作,N 节点为最低失衡点。(N,K,M)为最小不平衡子树
1.1. 在平衡的二叉排序树(AVL)中插入一个节点,当出现不平衡时,根据不平衡情况可分为四种不平衡类型 ,这四种类型又可通过两类操作"单旋,双旋"来实现复衡
假设已知 最低失衡点 为A,根据新插入节点与A的位置关系来命名不平衡类型
- LL型:新插入节点在A的左孩子(L)的左子树(L)中;
- LR型:新插入结点在A的左孩子(L)的右子树(R)中;
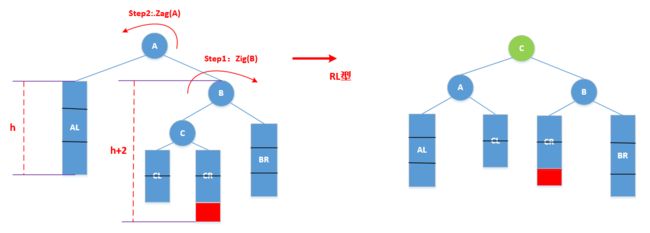
- RL型:新插入结点在A的右孩子(R)的左子树(L)中;
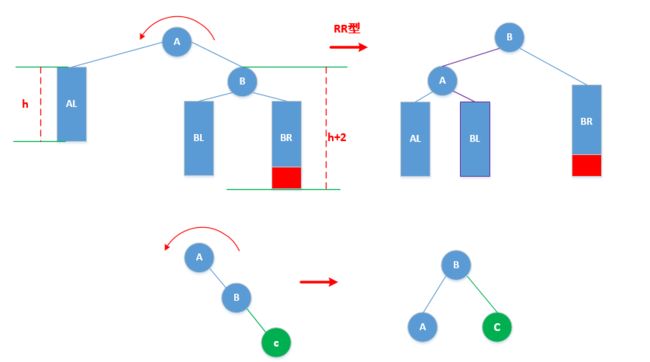
- RR型:新插入结点在A的右孩子(R)的右子树(R)中;
图解这四种类型,以及其复衡操作
LL型 : 右旋最低失衡点A(Zig(A))
RR型 :左旋最低失衡点A(Zag(A))
LR型 :
RL型 :
下面通过更详细的"单旋,双旋操作步骤"来展示实现4类失衡情况复衡的过程
单旋 :
- 对于 LL型 : 只需对
最低失衡点A进行Zig(A)操作 - 对于 RR型 :只需对
最低失衡点A进行Zag(A)操作
本质上是一次等价变换的实现过程
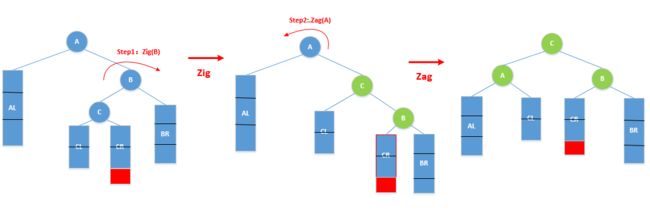
- 以RR型为例,Zag(A)的等价变换过程
- 本质上是等价交换的过程,将
三个节点及其子树按中序次序重构即可
[注] 理解上,采用上面的"RR型"图示展示的"2个节点+3棵子树"来重新构建即可,但是下面双旋要以3+4结构来实现重构,所以单旋'委屈一下'适应双旋,以便后续重构算法的统一实现,而不是单旋写一个重构,双旋也实现一个重构。
双旋 :
- 对于 LR型 : zag-zig
- 对于 RL型 : zig-zag
与单旋类似,本质上也是等价变换的过程
- 以 RL型为例,进行 zig-zag 操作的过程
- 上图中
失衡前的树(1)到复衡后的树(3),本质上就是等价交换的过程:即
A,B,C三个节点与其对应的子树,按中序次序重新构建,可恢复平衡
将上述的单旋,双旋的操作过程理解清楚,本质上是等价交换的过程,下面的代码实现也是基于这个思想,理解了这个过程,也就理解了下述复衡算法实现的过程 。
重点!!!
插入操作代码实现:
/*************************************/
#define FromParentTo(x) ( IsRoot(x) ? _root : ( IsLChild(x)? x.parent->lchild : x.parent->rchild) )
BinNodePosi insert(const T & e)
{
BinNodePosi &x = search(e); //查找插入点
if (x)
{
return x; //若目标已经存在,不执行插入操作,直接返回
}
x = new BinNode(e, _hot); //找到待插入点,以_hot为父亲,创建 x ,并插入
_size ++;
BinNodePosi xx = x;
//以下,从 x 的 父亲出发,逐层向上,依次检查各代祖先,找到最低失衡点
for (BinNodePosi g = x->parent; g; g = g->parent)
{
if (!AvlBalanced(*g)) // 一旦发现g失衡,则找到最低失衡点,通过调整可恢复全树平衡
{
//具体的重平衡实现函数
FromParentTo(*g) = rotateAt( tallerChild(g) ); //旋转重平衡操作
break;
}
else
{
//否则,只需要更新其高度(平衡度虽然不变,高度却有可能改变)
updateHeight(g); //是只要更新该节点高度,还是包括其祖先??再整理一下
}
}
return x; //返回新节点,只需要一次调整!!!;
}
2. AVL删除节点操作
当出现不平衡状态需要重平衡时,同样通过"单旋"和"双旋"两类操作实现
- 单旋 : LL型 和 RR型
- 同时至多一个失衡节点g,首个可能的就是删除节点 x 的父亲节点 _hot
- g经过单旋调整后恢复平衡,子树高度
未必复原,更高祖先仍可能失衡- 因有
失衡传播现象,可能需要做 O(log n)次调整
- 双旋 : zig-zag 和 zag-zig
以 zag-zig 为例:
- 同时至多一个失衡节点g,首个可能就是删除节点x的父亲_hot
- Zag(p)
Zig(g)- 因有
失衡传播现象,可能需要做 O(log n )次调整
删除操作代码实现:
/*************************************/
bool remove(const T &e)
{
BinNodePosi & x = search(e);
if ( !x )
{
return false; //待删节点不存在
}
removeAt(x, _hot); //按常规的BST规模删除之后,_hot及其祖先都有可能失衡
_size --;
//以下是删除后的重平衡操作:从_hot出发逐层向上,依次检查其祖先g
for (BinNodePosi g = _hot; g; g = g->parent)
{
if ( !AVLBalanced(*g) ) //一旦找到失衡点,则通过调整恢复平衡
{
g = FromParentTo(*g) = rotateAt( tallerChild( tallerChild(g) )); //旋转重平衡操作
}
upDateHeight(g); //并更新其高度
} // 可能还需做多次调整!!!无论是否做过调整,全树高度均可能下降
return true;
}
上面AVL插入和删除节点操作,重平衡讲的很热闹
那么重平衡算法rotateAt()函数(也就是旋转操作)到底是怎么实现的呢?
我们现在知道所谓的旋转操作rotateAt()无外乎zig, zag, zig-zag, zag-zig四类
那么如何能够高效的实现上述四类旋转呢?
通过一些分析,不难发现,所谓旋转最后实现的复衡结构,实际上是满足中序次序的重新构建,将理解上的旋转操作转换成逻辑上的构建操作,复衡算法的实现也就很容易实现
下面着重讲解!
写在前面
/* 删除节点操作后的调整动作 */
/* 1. <3+4重构> */
BinNodePosi connect34(BinNodePosi, BinNodePosi, BinNodePosi,
BinNodePosi, BinNodePosi, BinNodePosi, BinNodePosi);
/*2. <旋转操作> */
BinNodePosi rotateAt(BinNodePosi);
"3+4" 重构算法
前面提及的 zig ,zag 操作(单旋式,双旋式),主要是帮助对算法操作过程形成整体了解,在真正的实现时,我们不必机械地如此理解,通过上面的图示,也很容易看出复衡的过程,也就是 3个节点 + 4棵子树的重新组合构建的过程
AVL 重平衡过程:并非在乎平衡过程的技巧,更在于高效率实现重平衡,引入高效重平衡算法"3+4" 重构算法
"3+4" 重构算法
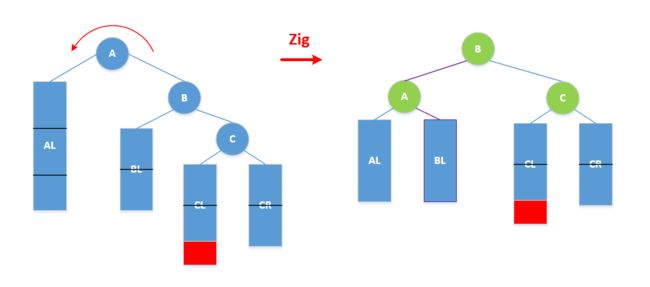
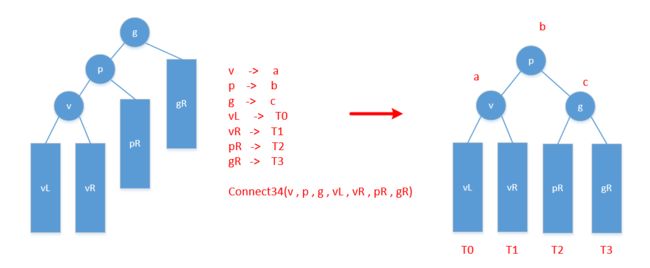
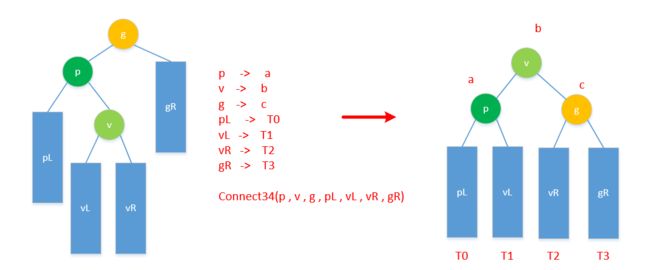
- 设 g 为最低失衡节点,考察祖孙三代 g ~ p ~ v
以中序遍历次序(大小),将其重命名为 : a < b < c (g,p,v根据中序次序对号入座)
比如 LL 型 : {v,p,g} 对应 {a,b,c}
比如 LR 型: {p,v,g} 对应 {a,b,c}
此为 '3' , 表 3 个节点 - {g,p,v}总共拥有互不相交的四颗(可能为空)的子树,
按中序遍历次序,将其重命名为 T0 < T1 < T2 < T3
此为 '4' , 表 4 棵子树 - 重构 :
- a 的左子树为 T0,T0的父亲为a
a 的右子树为 T1,T1的父亲为a - c 的左子树为 T2,T2的父亲为c
c 的右子树为 T3,T3的父亲为c - b 的左孩子为 a,a 的父亲为 b
b 的右孩子为 c,c 的父亲为 b
- a 的左子树为 T0,T0的父亲为a
"3+4" 重构算法代码实现:
BinNodePosi connect(BinNodePosi a, BinNodePosi b, BinNodePosi c,
BinNodePosi T0, BinNodePosi T1, BinNodePosi T3, BinNodePosi T4)
{
//重构
a->lChild = T0;
if (T0)
{
T0 -> parent = a;
}
a->rchild = T1;
if (T1)
{
T1 -> parent = a;
}
updateHeight(a);
/**********************************************/
c->lChild = T2;
if (T2)
{
T2 -> parent = c;
}
c->rChild = T3;
if (T3)
{
T3 -> parent = c;
}
updateHeight(c);
/**********************************************/
b->lChild = a;
a->parent = b;
b->rChild = c;
c->parent = b;
updateHeight(b);
return b; //该子树新的根节点
}
统一调整 : 实现全树的复衡 rotateAt() 旋转操作
BinNodePosi rotateAt(BinNodePosi v)
{
BinNodePosi p = v->parent; //父亲
BinNodePosi g = p->parent; //祖父
if ( IsLChild(*p) ) // L
{
if (IsLChild(*v)) // L-L型
{
p-parent = g->parent; //向上联接
// 将 v, p, g 节点及其子树按中序排一下,作为入参
return connect34(v, p, g, v->lchild, v->rchild, p->rchild, g->rchild);
}
else // L-R型
{
v->parent = g->parent; //向上联接
return connect34(p, v, g, p->lchild, v->rchild, v->rchild, g->rchild);
}
}
else
{ // zag-zig , zag-zag
}
}
以 LL 型 和 LR 型为例,
[ 注 ] :
3+4重构的等价变换算法是为了统一解决单旋和双旋对应的等价变换的!!!诚然单旋LL型或RR型用2+3重构也可以实现等价变换,但是双旋的话却不能以2+3实现,必须多引入一个节点,只能采用3+4,为统一实现单旋&双旋,采用3+4,对于单旋无影响。
综合评价
- 优点 : 无论
search(),insert().remove(),最坏情况下的复杂度均为O(log n),O(n)的存储空间 - 缺点 : 借助
高度或平衡因子,为此需改造元素结构,或额外封装
实测复杂度与理论值尚有差距
插入/删除后的旋转,成本大
删除操作重平衡,最多需要Ω(log n) 次
如果需要频繁插入和删除操作,未免得不偿失
单次动态调整后,全树的拓扑结构的变化量可能高达Ω(log n)
`