_rsx
_rsx

CF467D. Fedor and Essay

不难看出，这是一道图论的题，只要要求在\(r\),的个数最小时，\(r\)的个数与文章长度。

预备知识

  • STL之map (内置应该是hash之类的)
  • tarjan缩点
  • 树形dp
  • 简单字符串
  • 邻接表存边

问题分析

由于同义是单向的，我们建起了单向边，容易的是，如果一个单词可以最后回到他自己，那就把这个环上的点缩成一个scc,记下每个scc的最优\(r\)和最优\(leg\)(即\(length\)但我由于个人原因更喜欢用\(lgh\))

在对我们所得的每一个强连通，进行重构图。最后跑一个\(dp\)即可(可以用深搜实现)

统计答案时，对每一个word独立操作即可

如果你还是不太清楚，我们再来看图(样例一)

我们先建一个对应关系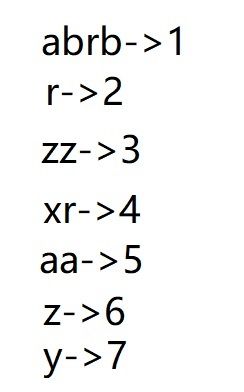CF467D. Fedor and Essay_第1张图片

然后，我们间的图即为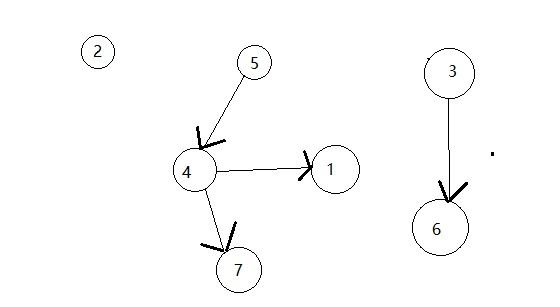CF467D. Fedor and Essay_第2张图片

然后，我们先进行缩点，然后统计出每个强连通的最优值，最后跑一遍树形dp就可以了

其实只要看清楚这个题的意思，就很好AC了

时间复杂度分析

  1. tarjan O(n+m)
  2. 统计最优值 O(n)
  3. 树形dp O(n)

好的没有毒瘤\(n^2\) ，此题可过

附上代码

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int Maxn=1e5+1;
map wd2;
int num,n,m,cnt,leg[Maxn],r[Maxn],h[Maxn],vcnt,col[Maxn],dfn[Maxn],low[Maxn],dep,sta[Maxn],top;
bool fsta[Maxn],flag[Maxn];
long long ans1,ans2;
string word[Maxn],str1,str2;
struct Edge{
    int fr,to,lac;
}edge[Maxn];
struct Node{
    int rmin,legmin; 
}scc[Maxn];
int read(){
    int x=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch<='9'&&ch>='0'){
        x=(x<<1)+(x<<3)+(ch-'0');
        ch=getchar();
    }
    return x;
}
char me(char ch){
    if(ch>='A'&&ch<='Z') ch+=32;
    return ch;
}
void insert(int x,int y){
    edge[vcnt].fr=x;
    edge[vcnt].to=y;
    edge[vcnt].lac=h[x];
    h[x]=vcnt++;
}
string Getstr(){
    string str;
    char ch=getchar();
    while(!((ch>='A'&&ch<='Z')||(ch>='a'&&ch<='z'))){
        ch=getchar();
    }
    while((ch>='A'&&ch<='Z')||(ch>='a'&&ch<='z')){
        str+=me(ch);
        ch=getchar();
    }
    return str;
}
void make(string str){
    leg[cnt]=str.size();
    for(int i=0;i<=str.size();i++){
        if(str[i]=='r') r[cnt]++;
    }
    return ;
}
void sol(string str){
    if(wd2[str]==0){
        wd2[str]=++cnt;
        make(str);
    }
}
void tarjan(int u){
    dfn[u]=low[u]=++dep;
    sta[++top]=u;fsta[u]=1;
    for(int i=h[u];i!=-1;i=edge[i].lac){
        int to=edge[i].to;
        if(dfn[to]){
            if(fsta[to]) low[u]=min(low[u],dfn[to]);
            continue;
        }
        tarjan(to);
        low[u]=min(low[u],low[to]);
    }
    if(low[u]==dfn[u]){
        num++;
        while(fsta[u]){
            fsta[sta[top]]=0;
            col[sta[top--]]=num;
        }
    }
    return ;
}
void dfs(int u){
    flag[u]=1;
    for(int i=h[u];i!=-1;i=edge[i].lac){
        int to=edge[i].to;
        if(!flag[to]) dfs(to);
        if(scc[to].rmin<=scc[u].rmin){
            if(scc[to].rmin str 每个str的号->对应str 
// wd2 str-> int 每个strstr对应 号 
//  freopen("puditan.in","r",stdin);
    m=read();
    for(int i=1;i<=m;i++) {
        word[i]=Getstr();
        sol(word[i]);
    }
    memset(h,-1,sizeof h);
    n=read();
    for(int i=1;i<=n;i++){
        str1=Getstr(),str2=Getstr();
        sol(str1);sol(str2);
        insert(wd2[str1],wd2[str2]);
    }
    for(int i=1;i<=cnt;i++) 
        if(!dfn[i]) 
            tarjan(i);//cnt指节点个数 
    for(int i=1;i<=num;i++) scc[i].legmin=0x3f3f3f3f,scc[i].rmin=0x3f3f3f3f;//num是强连通 
    for(int i=1;i<=cnt;i++)
        if(scc[col[i]].rmin>=r[i]){
            if(scc[col[i]].rmin>r[i])  scc[col[i]].legmin=leg[i];
            else scc[col[i]].legmin=min(scc[col[i]].legmin,leg[i]);
            scc[col[i]].rmin=r[i];
        }
    int q=vcnt;
    vcnt=0;
    memset(h,-1,sizeof h);
    for(int i=0;i

感想 ，这道题拖了很久没做，还是内心的惧怕呀

你可能感兴趣的:(CF467D. Fedor and Essay)

  • 利用ChatGPT辅助撰写课题申报书中的研究框架与内容设计全攻略指南 智写AI AI学术写作指南chatgpt人工智能AIGCAI写作论文笔记
    欢迎关注EssayBot，为大家带来最酷最有效的智能AI学术科研写作攻略。关于使用ChatGPT等AI学术科研的相关问题可以和作者七哥沟通：yida985撰写课题申报书是启动科研项目的第一个步骤，而研究框架与内容设计又是这一过程中的关键要素，它们对课题申报的成功起着决定性作用。研究框架为整个项目提供了一个宏观的结构蓝图，而内容设计则细化了研究活动的每个具体步骤。借助ChatGPT可以更高效地构建和
  • el-radio-group样式自定义 懒人w 工作记录随笔笔记前端elementui
    效果图[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tirq7Q04-1687314122585)(/images/essay/essay-0.1.png)].ai-tab-change{//中部按钮样式.el-radio-button__inner{//width:82px;//height:36px;border-radius:10px10px10px10px;
  • 【2025考研英语高分写作：20大必备范文】经典范文053 社会热点:健康 P177 HitTheBooks 考研
    Directions:Writeanessaybasedonthefollowingchart.Inyourwriting,youshould1)interpretthechart,and2)giveyourcomments.Youshouldwriteabout150wordsontheANSWERSHEET.Thelinechartaboveillustratesclearlytheamoun
  • [大译] Apply Aristotle's first principles to businesses 亚里士多德第一原则用于企业 苹果放阳台
    informationsource问文章出处:https://www.inc.com/peter-economy/elon-musk-netflix-both-use-this-ancient-mental-strategy-to-succeed.htmlAristotle'sfirstprinciplessaysthemoreyouknowaboutsomething'sfundamentalp
  • 如何写就一篇好的essay 利维坦trs
    Step1：做好时间安排在进行写作前，请先制定时间计划表，这一点似乎不太被重视但却十分重要。时间安排分为两个维度：纵向上安排好每天学习与其他活动的时间；横向上安排好处理essay每个部分的时间。一方面essay写作考察学术研究能力，另一方面考察文字编辑能力（如何能将想法简明扼要集中表达？如何准确表达出有力观点？）。如果你不擅长学术研究，请多从最新研究成果以及经典表述中碰撞出思路，同时保留足够的文字
  • 7/3 Learning essay of probability rusty6kimo
    TodayIlearnedanothernicepropertofPascal'striangle.ChoosingKpeoplefromNpeopleequalstothenumberofwaysofchoosingk-1peoplefromN-1people,plusthenumberofwaysofchoosingKpeoplefromN-1people.It'seasyandveryint
  • 2018年12月四级真题作文范文（毕业后的创业挑战） GT1100ti
    2018年12月大学英语四级考试如期结束，相信参加了考试的小伙伴们感触良多，由于考题是多题多卷，先别急着去放松，我们首先来回顾下你考的是哪一版吧。英语四级【考卷一】Directions:Forthispart，youareallowed30minutestowriteashortessayonthechallengesofstartingacareeraftergraduation.Youshou
  • 《爱情笔记》Essays in love - 10 译嘉
    10SpeakingLove爱的表白1.InthemiddleofMay,Chloecelebratedhertwenty-fourthbirthday.ShehadforalongtimebeendroppinghintsaboutaredcashmerepulloverinthewindowofashopinPiccadilly,sothedaybeforethecelebration,Ibo
  • 留学生乱用ChatGPT真的太致命！被认定学术不诚信直接被退学 do1twe11 chatgpt人工智能
    01.ChatGPT留学生神器？作业论文全靠它？近期留学圈内最火热的话题，肯定是关于ChatGPT。“这个python作业我写不来，让ChatGPT帮我直接生成code就好了。”“论文英文的写不来，ChatGPT直接生成一篇essay，简直就是教授级别的论文了。”“这个作业也太难了吧，问问ChatGPT！”相信很多留学生都有听闻过这些话语，肯定也有很多同学尝试过ChatGPT有不少同学声称，他们使
  • Abomination - Character Development Harry哈利
    ThisarticleisaboutabookIrecentlyfinishedreadingatschool.ItiscalledAbomination.TheauthorisRobertSwindellsandhereallyputsomethoughtandcoolplottwistsinthisbook.Ihavewrittenanessayaboutsomethingthatreally
  • ENVS363 A Computational Essay zhuyu0206girl 学习方法
    ENVS363/563.3-AComputationalEssay2023/24OverviewandInstructionsDueDate:8thJanuary202450%ofthefinalmarkOverviewHere’sthepremise.Youwilltaketheroleofareal-worldGISanalystorspatialdatascientisttaskedtoex
  • 2018-11-11 TOEFL Writing 10天突破新托福Essay Day 4---Leisure suntarliarzn
    Artsbringyouhopewhenyoufeelhopeless,giveyoucomfortwhenyouareanxiousandsupportyouwhenyouaredefeated.------Robinlandscapepaintingcn.风景画representationalpaintingcn.具象画mural/frescocn.壁画Differentstrokesford
  • 爬取猫眼信息 敬德修业－自强不息 python
    importrequestsfromfake_useragentimportUserAgentimportjsonimportpymongo#保存到数据库clien=pymongo.MongoClient(host='填写数据库IP')db=clien.The_cat_s_eye_essaycoll=db.eye_essay#创建一个随机生成user-aengt的对象ua=UserAgent()#
  • 有没人曾告诉你，商科Essay这么写！ Essay写写写
    1、审题审题在各类Essay写作当中非常重要，因为如果没审好题，没有理解老师的作业要求，那么写出来的东西肯定是与主题相去甚远，这样浪费了时间精力，连基本分都保证不了，所以还不如一开始弄清楚文章要干什么，怎么样可以达到这个目的。下面就以一个金融本科的essaytask为例，来说一下怎么审题。分析这道作业要求可以得出以下几点：(1)自己选一个知名公司为其提供咨询，要收集足够信息对这个公司进行分析。(2
  • 手机时代的聚会 一匹马来了
    Direction:Writeanessayof160-200wordsonthefollowingpicture.inyouressay,youshould1)describlethepicturebriefly2)interpretitsintendedmeaning3)giveyourcomment2015考研英语1Aswecanseeinthepicture,alltheteenagers
  • 5个维度解析2023高考作文题目 QYDY2020
    2023年全国高考[thenationalcollegeentranceexam]正式拉开大幕，1291万考生[12.91millionstudents]赶赴考场，迎接人生路上的一次大考。随着语文[theChineselanguage]考试[test]的结束，备受关注的各地高考作文题目[essaytopics]已经新鲜出炉！【freshlyreleased】全国甲卷试题内容：阅读下面的材料，根据要
  • 读懂诗歌：Louise Glück 系列学习（四）艺术之梦是通往被隐藏世界的小径 Annie灵兮
    露易丝·格丽克——《诗歌像一座灯塔，不同的是当游向它时，它就后退》作者：露易丝·格丽克译者：柳向阳来源：ProofsandTheories.EssaysonPoetry作家的根本体验是无助。这并不是说要将写作与活着相区分，而是说要纠正那种幻想，即认为创作就是一路高歌，得心应手，认为作家是一些运气好、能够做自己希望做的事情的人：信心十足，定期将他写在一张纸上的玩意拿去打印。但写作并不是个性的倾泻。而
  • 15th July English oral learning essay rusty6kimo
    TheyfinallydecidedtheirteamnamewouldbeArmyAnt.BecauseSheldonintendedtothreatenthemthathewasgoingtoquitifhedidn'tgethiswaywhichistheteamnamedidn'tgoforArmyAnt.PennywaswonderingifRajcouldanswerthequesti
  • 2020年英语六级作文真题 Johansong
    2020年英语六级作文真题2020年12月第1套：交流技巧作文题目：Directions:  Forthispart,youareallowed30minutestowriteanessayonwhystudentsshouldbeencouragedtodevelopeffectivecommunicationskills.Youshouldwriteatleast150wordsbutnomo
  • 2022-2023学年英语周报九年级第5期答案汇总 gaokaos
    However,ifyourestrictyourselftonovels进入查看：2022-2023学年英语周报九年级第5期答案汇总以下内容仅作展示，图片上方文字进入查看。However,ifyourestrictyourselftonovelsyouwillmissalotoftreasures.Englishessayscanatonceinformyou,entertainyou,andi
  • 《爱情笔记》Essays in love - 22 译嘉
    22TheJesusComplex基督情结1.Ifthereisanybenefittobefoundinthemidstofagony,itmayperhapslieintheabilityofcertainsuffererstotakethismiseryasevidence(howeverperverse)thattheyarespecial.Whyelsewouldtheyhavebeen
  • 要说最有特色的侧脸，可能要数全职猎人的西索 数字游戏
    全职猎人的西索脸上画有泪滴状和星星状的妆，宛如一张“小丑脸”。来自FlawlessAya的设计。旧版发色前期是绿发，后期变为红发。新版只出现了红发。来自Debbiichan的设计。从侧面看，竖起的头发如同火焰，这和他反复无常、喜欢战斗的性格匹配。来自Nel-Nelart的设计。他具有变化系念能力，能施展“伸缩自如的爱”及“轻薄的假象”。来自Callyzah的设计。一般情况下，他的头发是竖起的，洗澡
  • CF1446B Catching Cheaters 题解 DP BestMonkey 题解算法c++c语言
    CatchingCheaters传送门题面翻译给我们两个字符串，让我们从中选出两个字串，算出它们的最大公共子序列长度。然后将它乘444在减去两个字串的长度。问你这个数最大是多少。题目描述YouaregiventwostringsAAAandBBBrepresentingessaysoftwostudentswhoaresuspectedcheaters.ForanytwostringsCCC,DD
  • 讲解：FCC Film、Python/JAVA、C/C++、githubR|R 日青天
    FCCFilm1EssayPromptDefiningFormandMeaningviaIntertextualReferences(500)DaysofSummerandTheGraduateThequestionsbelowarenotrequiredforyoutoanswer,butwillguideyouinyouressay.Useyourknowledgeofbothfilmstoh
  • 那年今日 岩之鹰J
    “景色中最丰富的元素，就是一点天真无邪的阳光。”1817年的今天，著名美国作家、哲学家亨利·戴维·梭罗出生。Todaymarksthe202ndbirthanniversaryofHenryDavidThoreau,whowasanAmericanessayist,poetandphilosopherbestknownforhisbookWalden,areflectionuponsimpleli
  • 自闭Day47 | 喘不过气 想要勇気
    两点多就能上床，真是太早了这几天日夜颠倒，每天四五点才睡，甚至四五点都不困，然后中午午饭时间才起回家几天，忙vidéoessay忙kira忙哥大ddl真的感觉已经不是人是游魂了，但就是有强大的力量让我半夜练啊练，一次又一次地录，因为真的是must-to-do哥大的kira本来录完还挺洋洋自得的，想着居然问我这么正中下怀的问题。直到第二天醒来感觉不太对，查了一下interstaterelations
  • 《爱情笔记》Essays in love - 17 译嘉
    17Contractions挛缩1.Thoughquestionsofrealityandfalsehoodinthisareaarenotoriousforresistingscrutinyandsystematicanalysis,afterourreturnfromSpainIbegantosuspect?withoutquitebeingabletolookattheevidenceint
  • MSc assignment Digital Communication and signal processing (30059) weixin_33692284 matlabpythonjava
    Section1.DigitalCommunicationandsignalprocessing(30059)-MScassignment2018-19Theassignmentforms50%ofthefinalmark.1.Eachstudentshouldprepareabriefessaypresentedinascientificpaperformatandstyleonaspecifi
  • ENVS363 A Computational Essay _0206girl 学习方法网络
    ENVS363/563.3-AComputationalEssay2023/24OverviewandInstructionsDueDate:8thJanuary202450%ofthefinalmarkOverviewHere’sthepremise.Youwilltaketheroleofareal-worldGISanalystorspatialdatascientisttaskedtoex
  • 留学圈的作业代写有多严重？留学生essay写作黑色产业链解析 no_25f6
    留学圈的作业代写有多严重？留学生essay写作黑色产业链解析留学圈的代写现象比你想得还严重这样说吧，你加几个留学生微信群就知道了，里面几乎是二十四小时不停的代谢广告刷屏有的群原本是留学生聊天吹水分享生活学习经验的地方，自从放进几个中介后，这些中介又拉别的中介进群，过不了多久广告就刷屏刷起来了，一开始群主或者管理员还会出来踢人维护群内秩序，但是随着代写广告越来越多，慢慢的群主也放弃了，最终这个群被广
  • 如何用ruby来写hadoop的mapreduce并生成jar包 wudixiaotie mapreduce
    ruby来写hadoop的mapreduce，我用的方法是rubydoop。怎么配置环境呢： 1.安装rvm：     不说了 网上有 2.安装ruby：     由于我以前是做ruby的，所以习惯性的先安装了ruby，起码调试起来比jruby快多了。 3.安装jruby：     rvm install jruby然后等待安
  • java编程思想 -- 访问控制权限 百合不是茶 java访问控制权限单例模式
    访问权限是java中一个比较中要的知识点,它规定者什么方法可以访问,什么不可以访问   一:包访问权限;   自定义包: package com.wj.control; //包 public class Demo { //定义一个无参的方法 public void DemoPackage(){ System.out.println("调用
  • [生物与医学]请审慎食用小龙虾 comsci 生物
         现在的餐馆里面出售的小龙虾,有一些是在野外捕捉的,这些小龙虾身体里面可能带有某些病毒和细菌,人食用以后可能会导致一些疾病,严重的甚至会死亡.....      所以,参加聚餐的时候,最好不要点小龙虾...就吃养殖的猪肉,牛肉,羊肉和鱼,等动物蛋白质     
  • org.apache.jasper.JasperException: Unable to compile class for JSP: 商人shang maven2.2jdk1.8
    环境： jdk1.8    maven  tomcat7-maven-plugin  2.0 原因： tomcat7-maven-plugin  2.0 不知吃 jdk 1.8，换成 tomcat7-maven-plugin  2.2就行，即     <plugin>
  • 你的垃圾你处理掉了吗?GC oloz GC
    前序:本人菜鸟，此文研究学习来自网络，各位牛牛多指教　 1.垃圾收集算法的核心思想 　　Java语言建立了垃圾收集机制，用以跟踪正在使用的对象和发现并回收不再使用(引用)的对象。该机制可以有效防范动态内存分配中可能发生的两个危险：因内存垃圾过多而引发的内存耗尽，以及不恰当的内存释放所造成的内存非法引用。 　　垃圾收集算法的核心思想是：对虚拟机可用内存空间，即堆空间中的对象进行识别
  • shiro 和 SESSSION 杨白白 shiro
    shiro 在web项目里默认使用的是web容器提供的session，也就是说shiro使用的session是web容器产生的，并不是自己产生的，在用于非web环境时可用其他来源代替。在web工程启动的时候它就和容器绑定在了一起，这是通过web.xml里面的shiroFilter实现的。通过session.getSession()方法会在浏览器cokkice产生JESSIONID，当关闭浏览器，此
  • 移动互联网终端 淘宝客如何实现盈利 小桔子 移動客戶端淘客淘寶App
           2012年淘宝联盟平台为站长和淘宝客带来的分成收入突破30亿元，同比增长100%。而来自移动端的分成达1亿元，其中美丽说、蘑菇街、果库、口袋购物等App运营商分成近5000万元。 可以看出，虽然目前阶段PC端对于淘客而言仍旧是盈利的大头，但移动端已经呈现出爆发之势。而且这个势头将随着智能终端(手机，平板)的加速普及而更加迅猛
  • wordpress小工具制作 aichenglong wordpress小工具
    wordpress 使用侧边栏的小工具，很方便调整页面结构 小工具的制作过程 1 在自己的主题文件中新建一个文件夹(如widget)，在文件夹中创建一个php(AWP_posts-category.php) 小工具是一个类,想侧边栏一样，还得使用代码注册，他才可以再后台使用，基本的代码一层不变 <?php class AWP_Post_Category extends WP_Wi
  • JS微信分享 AILIKES js
    // 所有功能必须包含在 WeixinApi.ready 中进行    WeixinApi.ready(function(Api) {        // 微信分享的数据            var wxData = {       &nb
  • 封装探讨 百合不是茶 JAVA面向对象 封装
    //封装   属性 方法 将某些东西包装在一起，通过创建对象或使用静态的方法来调用，称为封装；封装其实就是有选择性地公开或隐藏某些信息，它解决了数据的安全性问题，增加代码的可读性和可维护性   在 Aname类中申明三个属性，将其封装在一个类中：通过对象来调用   例如   1： //属性 将其设为私有 姓名 name 可以公开
  • jquery radio/checkbox change事件不能触发的问题 bijian1013 JavaScriptjquery
    我想让radio来控制当前我选择的是机动车还是特种车，如下所示：  <html> <head> <script src="http://ajax.googleapis.com/ajax/libs/jquery/1.7.1/jquery.min.js" type="text/javascript"><
  • AngularJS中安全性措施 bijian1013 JavaScriptAngularJS安全性XSRFJSON漏洞
            在使用web应用中，安全性是应该首要考虑的一个问题。AngularJS提供了一些辅助机制，用来防护来自两个常见攻击方向的网络攻击。 一.JSON漏洞         当使用一个GET请求获取JSON数组信息的时候（尤其是当这一信息非常敏感，
  • [Maven学习笔记九]Maven发布web项目 bit1129 maven
    基于Maven的web项目的标准项目结构 user-project     user-core     user-service     user-web        src      
  • 【Hive七】Hive用户自定义聚合函数(UDAF) bit1129 hive
    用户自定义聚合函数，用户提供的多个入参通过聚合计算(求和、求最大值、求最小值)得到一个聚合计算结果的函数。 问题：UDF也可以提供输入多个参数然后输出一个结果的运算，比如加法运算add(3，5)，add这个UDF需要实现UDF的evaluate方法,那么UDF和UDAF的实质分别究竟是什么？   Double evaluate(Double a, Double b)  
  • 通过 nginx-lua 给 Nginx 增加 OAuth 支持 ronin47
    前言：我们使用Nginx的Lua中间件建立了OAuth2认证和授权层。如果你也有此打算，阅读下面的文档，实现自动化并获得收益。SeatGeek 在过去几年中取得了发展，我们已经积累了不少针对各种任务的不同管理接口。我们通常为新的展示需求创建新模块，比如我们自己的博客、图表等。我们还定期开发内部工具来处理诸如部署、可视化操作及事件处理等事务。在处理这些事务中，我们使用了几个不同的接口来认证： &n
  • 利用tomcat-redis-session-manager做session同步时自定义类对象属性保存不上的解决方法 bsr1983 session
    在利用tomcat-redis-session-manager做session同步时，遇到了在session保存一个自定义对象时，修改该对象中的某个属性，session未进行序列化，属性没有被存储到redis中。 在 tomcat-redis-session-manager的github上有如下说明： Session Change Tracking As noted in the &qu
  • 《代码大全》表驱动法-Table Driven Approach-1 bylijinnan java算法
    关于Table Driven Approach的一篇非常好的文章： http://www.codeproject.com/Articles/42732/Table-driven-Approach package com.ljn.base; import java.util.Random; public class TableDriven { public
  • Sybase封锁原理 chicony Sybase
           昨天在操作Sybase IQ12.7时意外操作造成了数据库表锁定，不能删除被锁定表数据也不能往其中写入数据。由于着急往该表抽入数据，因此立马着手解决该表的解锁问题。     无奈此前没有接触过Sybase IQ12.7这套数据库产品，加之当时已属于下班时间无法求助于支持人员支持，因此只有借助搜索引擎强大的
  • java异常处理机制 CrazyMizzz java
    java异常关键字有以下几个，分别为 try catch final throw throws 他们的定义分别为 try：    Opening exception-handling statement. catch：  Captures the exception. finally： Runs its code before terminating
  • hive 数据插入DML语法汇总 daizj hiveDML数据插入
    Hive的数据插入DML语法汇总1、Loading files into tables语法：1) LOAD DATA [LOCAL] INPATH 'filepath' [OVERWRITE] INTO TABLE tablename [PARTITION (partcol1=val1, partcol2=val2 ...)]解释：1)、上面命令执行环境为hive客户端环境下： hive>l
  • 工厂设计模式 dcj3sjt126com 设计模式
      使用设计模式是促进最佳实践和良好设计的好办法。设计模式可以提供针对常见的编程问题的灵活的解决方案。 工厂模式 工厂模式（Factory）允许你在代码执行时实例化对象。它之所以被称为工厂模式是因为它负责“生产”对象。工厂方法的参数是你要生成的对象对应的类名称。 Example #1 调用工厂方法（带参数） <?phpclass Example{ 
  • mysql字符串查找函数 dcj3sjt126com mysql
      FIND_IN_SET(str,strlist) 假如字符串str 在由N 子链组成的字符串列表strlist 中，则返回值的范围在1到 N 之间。一个字符串列表就是一个由一些被‘,’符号分开的自链组成的字符串。如果第一个参数是一个常数字符串，而第二个是type SET列，则   FIND_IN_SET() 函数被优化，使用比特计算。如果str不在strlist 或st
  • jvm内存管理 easterfly jvm
    一、JVM堆内存的划分 分为年轻代和年老代。年轻代又分为三部分：一个eden,两个survivor。 工作过程是这样的：e区空间满了后，执行minor gc，存活下来的对象放入s0, 对s0仍会进行minor gc，存活下来的的对象放入s1中，对s1同样执行minor gc，依旧存活的对象就放入年老代中； 年老代满了之后会执行major gc，这个是stop the word模式，执行
  • CentOS-6.3安装配置JDK-8 gengzg centos
    JAVA_HOME=/usr/java/jdk1.8.0_45 JRE_HOME=/usr/java/jdk1.8.0_45/jre PATH=$PATH:$JAVA_HOME/bin:$JRE_HOME/bin CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar:$JRE_HOME/lib export JAVA_HOME
  • 【转】关于web路径的获取方法 huangyc1210 Web路径
    假定你的web application 名称为news,你在浏览器中输入请求路径：  http://localhost:8080/news/main/list.jsp  则执行下面向行代码后打印出如下结果：  1、 System.out.println(request.getContextPath()); //可返回站点的根路径。也就是项
  • php里获取第一个中文首字母并排序 远去的渡口 数据结构PHP
    很久没来更新博客了，还是觉得工作需要多总结的好。今天来更新一个自己认为比较有成就的问题吧。 最近在做储值结算，需求里结算首页需要按门店的首字母A-Z排序。我的数据结构原本是这样的： Array ( [0] => Array ( [sid] => 2885842 [recetcstoredpay] =&g
  • java内部类 hm4123660 java内部类匿名内部类成员内部类方法内部类
         　在Java中，可以将一个类定义在另一个类里面或者一个方法里面，这样的类称为内部类。内部类仍然是一个独立的类，在编译之后内部类会被编译成独立的.class文件，但是前面冠以外部类的类名和$符号。内部类可以间接解决多继承问题,可以使用内部类继承一个类，外部类继承一个类，实现多继承。      &nb
  • Caused by: java.lang.IncompatibleClassChangeError: class org.hibernate.cfg.Exten zhb8015
    maven pom.xml关于hibernate的配置和异常信息如下，查了好多资料，问题还是没有解决。只知道是包冲突，就是不知道是哪个包....遇到这个问题的分享下是怎么解决的。。   maven pom:   <dependency> <groupId>org.hibernate</groupId> <ar
  • Spark 性能相关参数配置详解－任务调度篇 Stark_Summer sparkcachecpu任务调度yarn
    随着Spark的逐渐成熟完善, 越来越多的可配置参数被添加到Spark中来, 本文试图通过阐述这其中部分参数的工作原理和配置思路, 和大家一起探讨一下如何根据实际场合对Spark进行配置优化。   由于篇幅较长，所以在这里分篇组织，如果要看最新完整的网页版内容，可以戳这里：http://spark-config.readthedocs.org/，主要是便
  • css3滤镜 wangkeheng htmlcss
    经常看到一些网站的底部有一些灰色的图标，鼠标移入的时候会变亮，开始以为是js操作src或者bg呢，搜索了一下，发现了一个更好的方法：通过css3的滤镜方法。 html代码： <a href='' class='icon'><img src='utv.jpg' /></a> css代码： .icon{-webkit-filter: graysc
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他