后缀自动机构建图解

后缀自动机构建图解

我是在这学的：https://www.luogu.com.cn/blog/Kesdiael3/hou-zhui-zi-dong-ji-yang-xie

感觉作者画的图有点难理解，而且讲到了所以来画一画，方便复习。看本文前最好先把上面那个看一遍！

此处是从右往左增量，画图时没注意

代码：（注意case的位置）

struct NODE
{
    int ch[26];
    int len,fa;
    NODE(){memset(ch,0,sizeof(ch));len=0;}
}dian[MAXN<<1];
int las=1,tot=1;
void add(int c)
{
    int p=las;int np=las=++tot;
    dian[np].len=dian[p].len+1;
    for(;p&&!dian[p].ch[c];p=dian[p].fa)dian[p].ch[c]=np;
    if(!p)dian[np].fa=1;//以上为case 1
    else
    {
        int q=dian[p].ch[c];
        if(dian[q].len==dian[p].len+1)dian[np].fa=q;//以上为case 2
        else
        {
            int nq=++tot;dian[nq]=dian[q];
            dian[nq].len=dian[p].len+1;
            dian[q].fa=dian[np].fa=nq; 
            for(;p&&dian[p].ch[c]==q;p=dian[p].fa)dian[p].ch[c]=nq;//以上为case 3
        }
    }
}
char s[MAXN];int len;
int main()
{
    scanf("%s",s);len=strlen(s);
    for(int i=0;i

case1

首先处理好parent树信息：

int p=las;int np=las=++tot;
dian[np].len=dian[p].len+1;

case1就是直接接到根上，下面为了方便理解把所有压缩的点都画出来了

实现方法（参照代码）：

for(;p&&!dian[p].ch[c];p=dian[p].fa)dian[p].ch[c]=np;
    if(!p)dian[np].fa=1;//以上为case 1

1. 新加进来的字符变量名为 \(c\)
2. 新建点 \(np(11)\)
3. 查看前面的点有没有能接上的，即有c这条出边
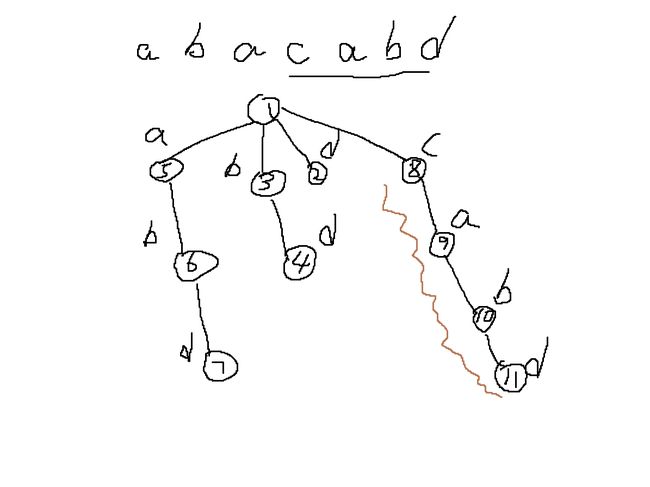
4. 这种情况为到根都没有，直接接上根点(1)

case2

前面有这个出边而且长度等于新后缀减一，此时直接连到后面。

这种情况很简单，因为只能是前一个后缀长度才能相差一

实现方法：

int q=dian[p].ch[c];
if(dian[q].len==dian[p].len+1)dian[np].fa=q;//以上为case 2

1. \(q(2)\) 为前面的有出边为 \(c\) 字符（此处 \(c\) 为'a'）的点
2. 长度符合，能接上，把\(np(3)\)直接接到\(q(2)\)

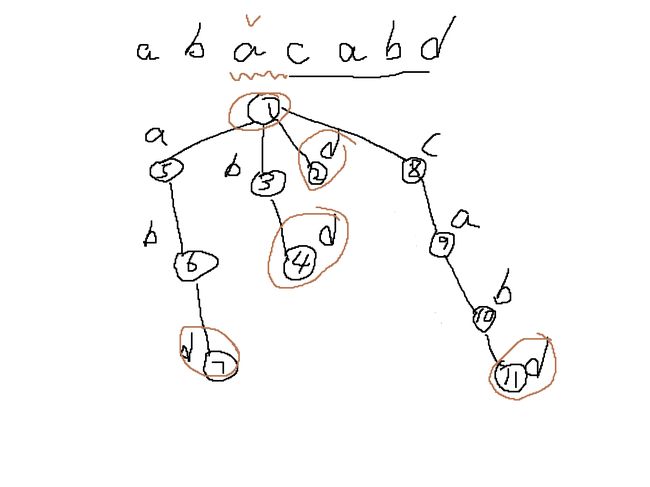
case3

回到case1的图，此时后缀自动机上真实存在的点只是红圈的点

现在加入 \(acabd\)，发现有根有 \(a\) 的出边，但是不能直接接上，因为实际上不存在5这个点。

也可以理解为5是被压缩的点。

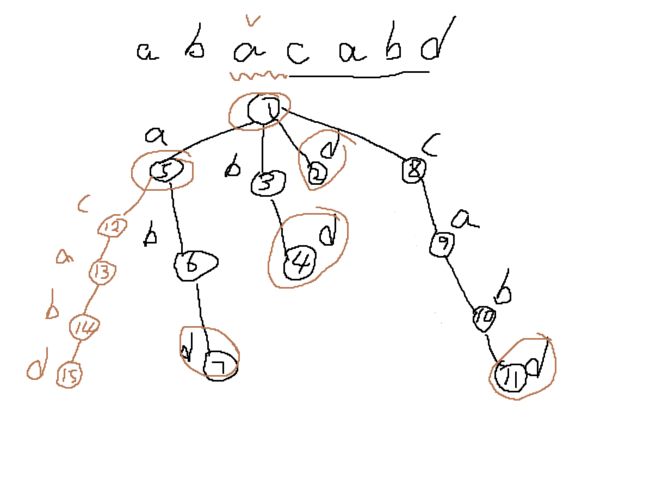
于是需要把 \(abd\) 这个等价类分成 \(a\) 和 \(abd\) 两个点 ，然后把 \(acabd\) 接到 \(a\) 上：

如图，a现在也变成了红圈点，这就是新建点的过程。

实现方法：

 else{
      int nq=++tot;dian[nq]=dian[q];
      dian[nq].len=dian[p].len+1;
      dian[q].fa=dian[np].fa=nq; 
      for(;p&&dian[p].ch[c]==q;p=dian[p].fa)dian[p].ch[c]=nq;//以上为case 3
 }

1. 新建点 \(nq(5)\)
2. 把 \(q(7)\) 的信息传给 \(nq(5)\) ：包括转移，parent树上父亲，等价类最大长度
3. \(nq(5)\) 最大长度此时为 \(len(p(1))+1=2\)，因为加了新增的字符 \(a\)
4. 把 \(q(7)\) 和 \(np(15)\) 的父亲置为 \(nq\)
5. 根据转移边要尽量近的原则，把原先a转移为 \(q(7)\) 的转移边连到 \(nq(5)\) 上（从 \(p(1)\) 开始）

做完了！やったぜ ~

感觉第一次真正理解了后缀自动机，图有点丑见谅啦