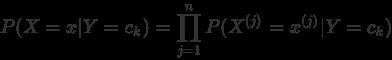Python 朴素贝叶斯法

朴素贝叶斯法是一种直观地方法，它使用每个属性归属于某个类的概率来进行预测。即在给定的已分类的数据集下，假设每个划分属性归属于某一类的概率是独立于其余属性，从而简化了概率的计算。通过计算这种强的独立性假设，来进行分类，这种分类是牺牲一定准确性的，但又是简单的。

1. 朴素贝叶斯法（naive Bayes）

1.1 基本方法

假设存在训练数据集![](http://latex.codecogs.com/svg.latex? \Large $T = {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)} $) 其先验概率分布为
![](http://latex.codecogs.com/svg.latex? \Large $$P(Y = c_k) = \frac{c_k}{N} $$)
其条件概率分布为![](http://latex.codecogs.com/svg.latex? \Large $$ P(X = x|Y = c_k) ,x = x^{(1)},x{(2)},...,x^{(N)} , k=1,2,...,K $$)

于是求的其联合概率分布为![](http://latex.codecogs.com/svg.latex? \Large $P(X,Y) = P(Y = c_k)P(X = x|Y = c_k)$)
在贝叶斯定义中，贝叶斯定理为

上式中分子部分的条件概率* P(X = x|Y = c_k)*的计算是极其复杂的，其复杂度是相对于变量个数成指数增长的，当存在很多特征的时候，计算的过程极其痛苦，如果再考虑分母展开的链规则的话，整个过程就会呈现一个组合爆炸的情况！

为此，朴素贝叶斯法就针对条件概率分布作出了条件独立性的假设，本文介绍的朴素贝叶斯也因此得名。

具体地，其条件概率计算公式如下：

相较于贝叶斯定义中的条件概率，此时参数减少了，也很好地避免了计算上的组合爆炸问题，对于属性数越多的问题，其运用就越简单，也越迅速。

由此可以习得的后验概率为：

![](http://latex.codecogs.com/svg.latex? \Large $$P(Y = c_k|X = x) = \frac{P(X = x|Y = c_k)P(Y=c_k)}{\sum_k{P(X = x|Y = c_k)P(Y=c_k)}} $$)

1.2 朴素贝叶斯分类器

基于此后验概率，即得到朴素贝叶斯分类器如下：

![](http://latex.codecogs.com/svg.latex? \Large $$ y= \arg\max_{c_k} P(X = x|Y = c_k)P(Y=c_k)$$)

1.3 离散变量和连续变量

对离散变量而言，条件概率公式为：

对连续变量而言，条件概率公式为：

其中σ是在c_k类下的标准差，μ为均值。

1.4 拉普拉斯修正

在

中，会存在某个

的情况，此时连乘会出现条件概率为0的情况，对此采用“拉普拉斯修正（ Laplacian correction）”进行“平滑（ smoothing）”。

在条件概率的式子下，将

为类别数。

2. 算法实现

以下列数据集为例，进行朴素贝叶斯算法的设计。

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	0.666	0.091	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	0.657	0.198	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.360	0.37	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

2.1 分类器简单设计

在这份数据中，“色泽”、“根蒂”、“敲声”、“纹理”、“脐部”和“触感”都为离散变量，而“密度”和“含糖率”为连续变量。利用pandas的DataFrame类型来对样本数据进行解析，相关代码如下：

import numpy as np
import pandas as pd

#获取各个类别条件概率
def get_pred(dataSet, inputSimple):
    p0classData = []#初始化类别矩阵
    p1classData = []
    classLabels = dataSet[dataSet.columns[-1]]#选取类别列
    for i in range(len(dataSet.columns) - 1):
        columnLabels = dataSet[dataSet.columns[i]]#特征列
        pData = pd.concat([columnLabels, classLabels], axis = 1)#拼接特征列和类别列
        classSet = list(set(classLabels))
        for pclass in classSet:
            filterClass = pData[pData[pData.columns[-1]] == pclass]#根据类别划分数据集
            filterClass = filterClass[pData.columns[-2]]
            if isinstance(inputSimple[i], float):#判断是否是连续变量
                classVar = np.var(filterClass)#方差
                classMean = np.mean(filterClass)#均值
                pro_l = 1/(np.sqrt(2*np.pi) * np.sqrt(classVar))
                pro_r = np.exp(-(inputSimple[i] - classMean)**2/(2 * classVar))
                pro = pro_l * pro_r#概率
                if pclass == '是':
                    p0classData.append(pro)
                else:
                    p1classData.append(pro)
            else:
                classNum = np.count_nonzero(filterClass == inputSimple[i])#计算属于样本特征的数量
                pro = (classNum + 1)/(len(filterClass) + len(set(filterClass)))#此处进行了拉普拉斯修正
                if pclass == '是':
                    p0classData.append(pro)
                else:
                    p1classData.append(pro)
    return p0classData, p1classData

上述代码是根据前文的朴素贝叶斯定义进行的设计，我们通过传入测试样本进行检验，测试样本如下：

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
测试1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	是

2.2 Scikit - Learn库简单实现朴素贝叶斯

在这份数据集中，由于离散的特征变量都为字符串，这里需要对其进行哑变量处理，即转化为数值型数据，以便后续的数值计算。

具体实现如下：

import pandas as pd

filename = 'data.txt'
dataSet = pd.read_csv(filename, sep = '\t', index_col = '编号')

#哑变量处理
featureDict = []
new_dataSet = pd.DataFrame()
for i in range(len(dataSet.columns)):
    featureList = dataSet[dataSet.columns[i]]
    classSet = list(set(featureList))
    count = 0
    for feature in classSet:
        d = dict()
        if isinstance(feature, float):#判断是否为连续变量
            continue
        else:
            featureList[featureList == feature] = count
            d[feature] = count
            count += 1
        featureDict.append(d)
    new_dataSet = pd.concat([new_dataSet, featureList], axis = 1)

处理完成的新数据集，通过Scikit - Learn库中的朴素贝叶斯模块进行训练和预测。

实现如下：

import numpy as np
from sklearn.naive_bayes import MultinomialNB

#设置训练数据集
X = [list(new_dataSet.ix[i][:-1]) for i in range(1,len(new_dataSet) + 1)]
Y = list(new_dataSet[new_dataSet.columns[-1]])

clf = MultinomialNB()#分类器
clf.fit(X, Y)#训练
predicted = clf.predict(X)
print('精度为：%f ' %np.mean(predicted == Y))

最终的准确度为：88.2353%，与前文的测试结果相近。

2.3 后期

朴素贝叶斯的优缺点如下：
优点：具有稳定的分类效率、能够处理多分类问题、算法简单，对缺失数据不敏感，常用于文本分类；

缺点：准确度受到各个特征独立的影响，在实际应用中并不一定存在这种假设，需要先验概率和样本本身决定后验概率从而决定分类，并不一定准确。

后期，笔者希望能够介绍一下如何使用Scikit - Learn库的朴素贝叶斯进行文本分类。

3. 参考文献

[1] 周志华. 机器学习.清华大学出版社，2016
[2] Peter Harrington. 机器学习实战. 人民邮电出版社，2013
[3] http://blog.csdn.net/lsldd/article/details/41542107