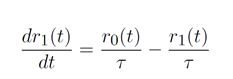信号与系统的模型:抓住主要矛盾,简化复杂的细节。
信号是什么?
系统输入输出的物理量,例如电路输出的电压或电流都是信号。信号是人为定义的,是人最关心的东西。通常来讲这些物理量都是时间的函数,因此信号本质上也是一个函数。
通常来讲输入为一种人为可控制的物理量,输出是输入经过系统后得到物理量。
系统是什么?
系统就是把复杂的东西抽象成只关心输入信号和输出信号的黑盒。
信号与系统的例子
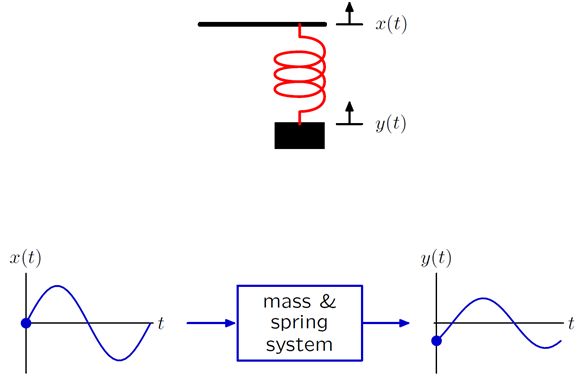
下面是一个弹簧重物系统,其中弹簧的上端是可移动的。输入信号X为上端移动到的位置,输出信号y为重物的位置。这就构成了一个系统,根据弹簧相关的物理学知识得到输入和输出之间的关系。假设施加上一定的输入通过系统的作用就能得到对应的输出信号。
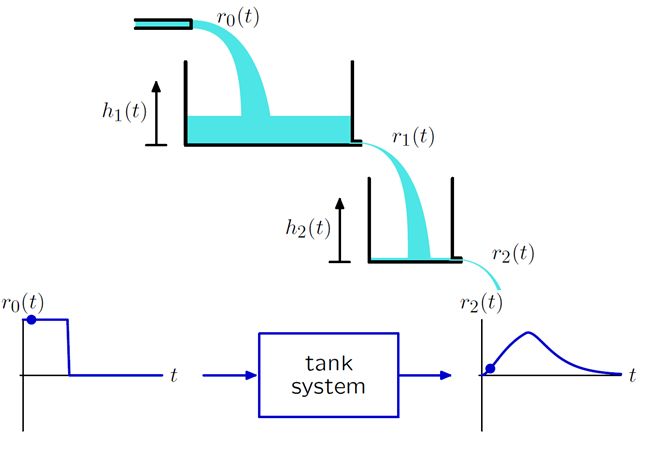
下图展示一个两个串联的蓄水池系统,输入为降雨量r0,输出为系统最终供应的水量r2。中间一些关于水位高度的物理量只是系统内部的变量,不是我们最关心的输入输出。
系统串联:多个系统可组成一个系统,一个系统内部可分为多个模块。
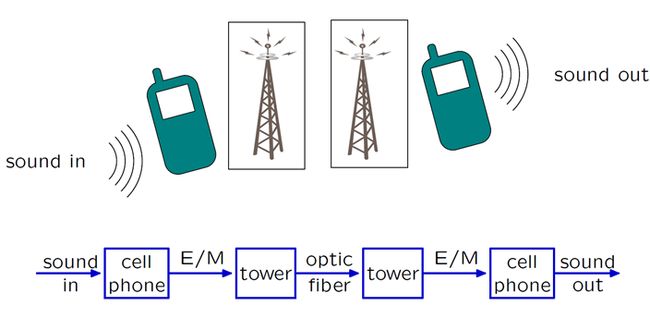
下图中举了个两个手机打电话的例子。语音信号需要先转化为电磁波发给基站,基站通过光纤将信号传给被叫用户所在基站,然后通过电磁波信号发给被叫用户设备,最终转化为声学信号。
该系统可看作多个系统串联起来形成的,也可认为是一个系统中有多个模块。
连续时间信号和离散时间信号
上述几个例子中的输入输出信号都是时间的函数。随时间变化的物理量可以是连续的,也可以是离散的。通常来讲实际物理量都是连续的,但离散的数字信号便于电子计算机系统能处理。显然,代数比微积分简单。
CT信号与DT信号中间的转化
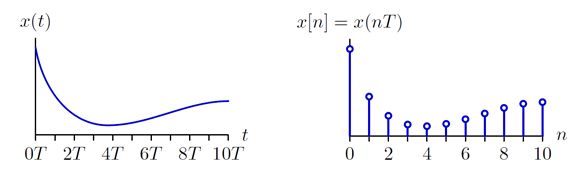
连续时间(CT)信号通过采样的方式可转化为离散时间(DT)信号。
在采样过程信号损失了一定的精度。因此DT信号恢复到CT信号过程中就需要"猜测"损失的信号。上述两个过程在电路中对应ADC模数转换和DAC数模转化。
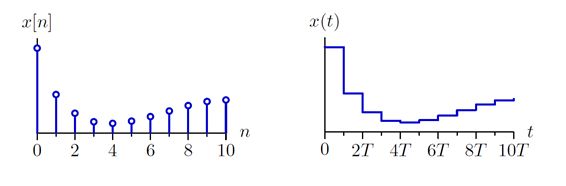
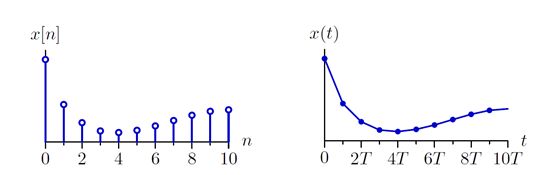
简单的DT恢复到CT的方法:
分段线性(piecewise linear)
零阶保持(zero-order hold)
例子:储水的水池和储电的电容
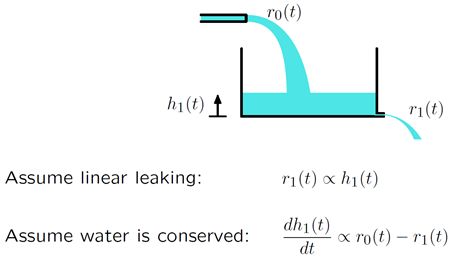
考虑下图所示储水池系统。关心的输入信号为r0,输出信号为r1。假设r1正比于水面高度h1。
水面高度 = (累计入 – 累计出 ) / 底面积。对该式子做微分后发现h1的导函数正比于r0 – r1。
上述两个关系带入一下就形成了下列关系式。其中存在一个与底面积呈正比的常数。这个常数单位为时间,在这里也被称为系统的时间常数。Y?
利用上述关系可在已知输入信号r0的情况下去求解输出信号r1。上述方程本质上是一个一阶线性微分方程。
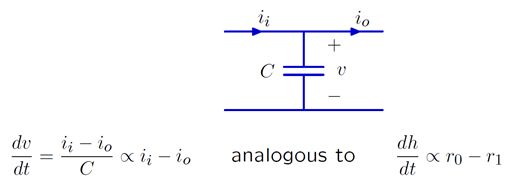
电容类比
与上述储水池类似,电容本质上是一个存储电荷的容器,其"底面积"和容量容量直接相关。
CT系统的近似解
上述水池和电容的例子都是CT系统。CT系统需要使用微分方程进行表示。复杂的微分可通过多种方法去求近似解,例如,欧拉法、反向欧拉法和中点法等。
详见微分方程的数字计算。
https://en.wikipedia.org/wiki/Numerical_methods_for_ordinary_differential_equations