在学习区块链的过程中经常会遇到密码学的概念,有时候会混淆本文将对以下概念进行简单解释:hash(哈希、散列)算法,数字摘要,对称加密,非对称加密,数字签名,Merkle树,同态加密(Homomorphic Encryption),零知识证明。
hash算法
简单来说就是把任意数据(二进制)变为固定长度的二进制,小到一个数字“1”,大到一个视频文件,只要是最终以二进制形式存储的数据,就能通过hash算法变为固定长度的一串数据。
一个优秀的hash算法有一下四个特点:
正面快速:就是说加密的速度要在有限时间和有限资源内完成,且越快越好。
逆向困难:就是说给你一个加密后的hash值数据,要想逆向破解获得加密前的明文是极其困难的。
输入敏感:明文只要发生哪怕一点点改变,进行hash运算后的值都会产生很大的改变。
冲突避免:不同的明文,他们进行hash运算后的hash值基本不可能一样。
冲突避免又叫做“抗碰撞性”,如果给你一个明文,得到hash值后,你无法找到另外一个明文的hash值与他一样,那么就叫做“抗弱碰撞性”。要是你自己随便找两个明文,让他们的hash值一样,如果做不到,那么叫做“抗强碰撞性”,也就是说具有更强的“抗碰撞性”。
现在比较流行的就是MD5和SHA-1算法。但是由于这两种算法不够安全,也就是在“抗碰撞性”上做得不够好,于是又有了SHA-224、SHA-256,SHA-512等算法。
比特币采用的SHA-256 hash算法,共有256位,也就是2的256次方个结果(这个数字十分巨大),产生新区快时候,由于hash逆向困难,旷工就要用哪一个值去跟新区块的hash的值碰撞,谁先猜对,就让谁在新的区块中写入信息,并且获得新区快中的奖励btc。
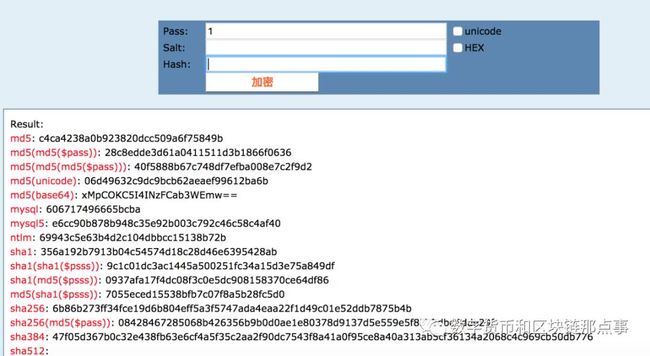
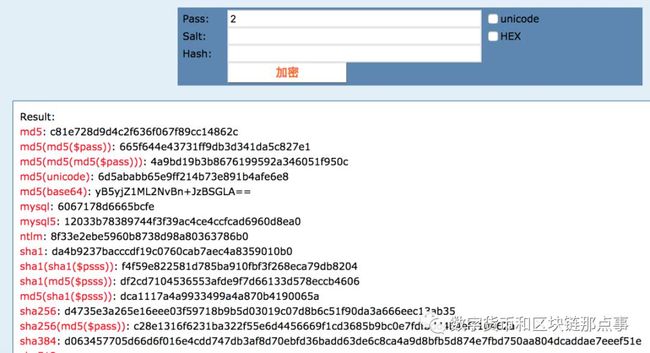
小张对“1”和“2”进行的hash算法,下面有很多种:md5,sha1,sha256等。
数字摘要
其实就是运用hash算法来对内容进行hash运算,由于前面说过了,一旦更改了原数据哪怕是一点点,hash值都会产生巨大的改变,所以这个数字摘要可以避免数据被篡改。
一个简单的实例就是比如小张要给你传一个文件,为了避免别人在文件中加入木马,小张就对文件进行数字摘要的获取,然后再单独把摘要(hash值)给你,当你拿到文件后,你也对文件进行跟小张一样算法的hash运算,如果得到的hash值跟小张传给你的一样,那么就证明文件没问题,可以打开,否则就证明被篡改了。
不光是比特币,数字签名还有更多更广泛的运用,比如之前介绍过的ULORD,就是把具有版权的数字化作品进行数字签名,然后把签名存储在公有链上,既能防止被串改,还能对版权进行控制。
在比特币交易中,当你要转账时候,需要把交易信息和一串数字签名一起传给矿工,矿工根据数字签名对你的交易信息进行校验,就如同上面说的一样,防止交易信息被篡改。
数字签名就是对信息的数字摘要进行了非对称加密而来。
接下来要说说加密算法中的对称和非对称加密。
加密算法
我们在加密过程中,要用加密算法和一个key来进行加密,举个最简单的例子,你要传送一个信息数字“1”给小伙伴,但是不想被别人知道,你就跟小伙伴约定:“我先把信息加上一个值,你拿到后再减去一个值就能得到原文(加密算法),这个值我每次跟你偷偷约定(key)”。比如这次约定的key是8,于是我就传一个“9”给小伙伴,同时告诉他,“key的值是8”,他拿到“9”后,再减去8就得到了原文“1”。
根据加密和解密时候的key相同或者不同,加密算法分为了对称加密和非对称加密。
对称密钥加密 (Symmetric Key Encryption)
特点:公钥(加密使用)、私钥(解密使用)相同。
优点:加密速度快,空间占用小,保密强度高。
缺点:key需要多方持有且高度保密,如果有一人泄露,信息就全部泄露了。
代表算法:DES、3DEA、AES、IDEA等。
适用场景:大量数据的加解密。
非对称加密(asymmetric encryption)
特点:公钥(加密使用)、私钥(解密使用)不同。
优点:公私钥分开,便于管理。
缺点:加密速度慢。
代表算法:RSA、EIGamal、椭圆曲线系列算法。
适用场景:签名、密钥协商场景。
实例:小张可以把公钥广播出去,需要跟小张通讯的人都可以用公钥对信息进行加密,小张拿到加密信息后,用自己独有的私钥进行解密,就能得到传给小张的信息了。
其实对称和非对称还可以组合适用,比如小张先用非对称加密把公钥给你,你把一个对称加密的临时秘钥加密了给小张,小张拿到这个对称加密的key后再对大量数据进行加解密处理。这样安全性和加解密速度都可以得到保障了。
数字签名
之前说了在比特币中,要用到数字签名校验交易信息是否是你发出。你使用比特币的时候都有一个私钥,你先把自己的交易信息进行hash运算取得数字摘要,然后用私钥对摘要进行非对称加密,接着把交易信息和加密后的数字签名一起发给旷工,矿工收到你的申请后,就用交易信息中的你的公钥进行解密得到数字摘要,然后再对加以信息进行hash,保证两个数字摘要一致,防止交易信息被篡改。这样既能保证交易信息没有被篡改,也能保证这笔交易确实是你发起的了。所以大家看出来了,保存好自己的私钥是多么重要的一件事。
Merkle树
默克尔树,又叫做哈希树。是一种二叉树。见下图。
简单说就是D0,D1,D2,D3。。。都是数据,他们两两内容进行hash后得到上面的节点N(i),最后得到总的节点Root。
特点就是:低层无论哪一个节点发生变动,都会向上传导,最终导致根节点发生变化。
应用场景:
1.快速比较大量的数据:如果两个默克尔树的根相同,就证明两个数据必然相同。
2.能够快读定位到变动的数据:比如D1有变化,就会影响N1,N4和Root,沿着Root - N4 - N1,可以快速定位到D1.
3.零知识证明:比如要证明数据中包含D0,但是又不想D0知道D1。。。D3的内容,这时就可以公布N0 - N4 节点,D0通过比对hash就能得到自己也在数据中,但是不知道其他内容。
同态加密
如果我们有明文A和明文B,我们分别对A、B进行加密得到密文C和D。我们把C和D进行相加,然后再用解密算法进行解密,一般情况下我们得到的解密结果都是无意义的信息。
但是同态加密就是说:我们对C+D进行解密后,得到的结果就是A+B的结果。
如果满足加减法就叫做加加法同态。
如果满足乘除法就叫做加乘法同态。
如果满足加减法又满足乘除法就叫做加全同态。
目前的算法例如:RSA满足乘法同态,Paillier满足加法同态,第一个全同态是09年才出现的Gentry算法。
这样的好处是:比如企业要用到云计算,但是又不想把数据公开出去。就可以把同态加密算法加密的密文发送到第三方云平台,等第三方计算完成后,取回本地进行解密操作。
大家可以看到不光是区块链,各行各业中密码学都是应用广泛,区块链更是把密码学运用到了的一个巅峰,要想好好了解区块链技术,了解密码学的一些基础知识还真是必不可少!