一、简介
Keras是有着自主的一套前端控制语法,后端基于tensorflow和theano的深度学习框架,因为其搭建神经网络简单快捷明了的语法风格,可以帮助使用者更快捷的搭建自己的神经网络,堪称深度学习框架中的sklearn,本文就将基于Keras,以手写数字数据集MNIST为演示数据,对多层感知机(MLP)的训练方法进行一个基本的介绍,而关于多层感知机的相关原理,请移步数据科学学习手札34:https://www.cnblogs.com/feffery/p/8996623.html,本文不再赘述。
二、利用Keras训练多层感知机
2.1 数据准备
由于keras.datasets中的mnist数据集获取方法为在线模式,目标网站在国内被墙了,所以这里提供另一种获取mnist数据集并读入的方式:
我们使用numpy中的load方法来读取npz格式的mnist数据集,下载地址在我的云盘中:链接: https://pan.baidu.com/s/13eBq9kmD0Vo6PMtfGVVlPQ 密码: xm77,下载完成后把mnist.npz文件放入keras模块的安装路径下的datasets文件夹中,这个自行去查找,例如我的路径就在D:\anaconda\Lib\site-packages\keras\datasets,找到路经后放入mnist.npz即可,接着在程序脚本中以下面的方式读入(因为mnist.npz文件中各个子数据集是以字典形式存放):
import numpy as np #因为keras中在线获取mnist数据集的方法在国内被ban,这里采用mnist.npz文件来从本地获取mnist数据 path = r'D:\anaconda\Lib\site-packages\keras\datasets\mnist.npz' with np.load(path) as f: X_train, y_train = f['x_train'], f['y_train'] X_test, y_test = f['x_test'], f['y_test']
通过上述步骤,我们就获得了我们所需要的数据。
2.2 数据预处理
在获得所需数据并成功读入后,我们需要做的是对数据进行预处理,因为本文只用到多层感知机来对mnist数据实现分类,并没有条件利用到每一个28X28格式手写数字灰度值样本的空间结构信息,所以需要将自变量进行从28X28到1X784的展开,并且由于输出目标为多类别,需要对因变量做one hot处理,并将全部数据转换为GPU运算支持的float32形式并归一化,相关代码如下:
#将格式为28X28的数据展开为1X784的结构以方便输入MLP中进行训练 RESHAPED = 784 '''将训练集与测试集重塑成维度为784,数值类型为float32的形式''' X_train = X_train.reshape(60000, RESHAPED).astype('float32') X_test = X_test.reshape(10000, RESHAPED).astype('float32') #归一化 X_train /= 255 X_test /= 255 #将类别训练目标向量转换为二值类别矩阵,即one-hot处理,传入单值,返回制定长度的向量表示形式 Y_train = np_utils.to_categorical(y_train, NB_CLASSES) Y_test = np_utils.to_categorical(y_test, NB_CLASSES)
至此,数据的预处理部分结束,下面正式进行MLP的模型搭建和训练过程;
2.3 第一个不带隐层的多层感知机模型
首先,导入相关模块和组件:
'''这个脚本以MNIST手写数字识别为例演示无隐层的多层感知机模型在Keras中的应用''' import numpy as np from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.optimizers import SGD from keras.utils import np_utils
接着,我们定义训练需要设置的一些必要参数:
'''设置随机数种子''' np.random.seed(42) '''网络结构参数预定义部分''' #定义训练轮数 NB_EPOCH = 40 #定义批尺寸 BATCH_SIZE = 128 #定义是否打印训练过程 VERBOSE = 1 #定义网络输出层神经元个数 NB_CLASSES = 10 #定义优化器 OPTIMIZER = SGD() #定义训练集中用作验证集的数据比例 VALIDATION_SPLIT = 0.2
现在到了最关键的网络结构搭建的部分,对于多层感知机,我们使用序贯模型Sequential来初始化,序贯模型的特点是网络的各组件按照其向后传播的路径来add,针对本例如下:
'''网络结构搭建部分''' #定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义输入层到输出层之间的网络部分 model.add(Dense(NB_CLASSES, input_shape=(RESHAPED,))) #为输出层添加softmax激活函数以实现多分类 model.add(Activation('softmax')) #打印模型结构 model.summary()
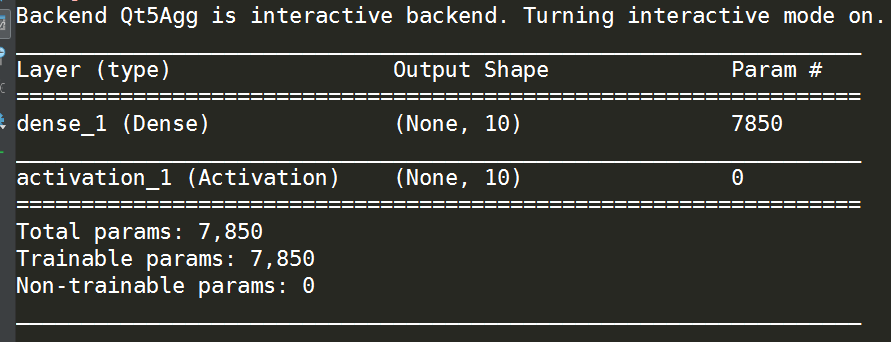
现在本例中的简单无隐层多层感知机就搭建完成,通过model.summary()我们可以看到网络结构如下:
可以看出每一层的结构非常清楚明了,这也是Keras的魅力所在,接着我们进行网络的编译,因为keras的后端是tensorflow或theano,所以需要将keras前端语言搭建的神经网络编译为后端可以接受的形式,在这个编译的过程中我们也设置了一些重要参数:
#在keras中将上述简单语句定义的模型编译为tensorflow或theano中的模型形式 #这里定义了损失函数为多分类对数损失,优化器为之前定义的SGD随机梯度下降优化器,评分标准为accuracy准确率 model.compile(loss='categorical_crossentropy',optimizer=OPTIMIZER,metrics=['accuracy'])
至此,网络的所有准备工作都已结束,下面进行正式的训练:
#进行训练并将模型训练历程及模型参数细节保存在history中,这里类似sklearn的方式,定义了自变量和因变量,以及批训练的尺寸,迭代次数,是否打印训练过程,验证集比例 history = model.fit(X_train ,Y_train, batch_size=BATCH_SIZE, epochs=NB_EPOCH,verbose=VERBOSE, validation_split=VALIDATION_SPLIT)
我们之前设置的训练迭代次数NB_EPOCH为40,又因为上面的fit代码中设置了verbose为1,即打印训练过程,所以得到结果如下(这里直接看第40轮迭代结果):
Epoch 40/40 128/48000 [..............................] - ETA: 1s - loss: 0.2974 - acc: 0.8906 3968/48000 [=>............................] - ETA: 0s - loss: 0.3158 - acc: 0.9115 7808/48000 [===>..........................] - ETA: 0s - loss: 0.3303 - acc: 0.9061 11776/48000 [======>.......................] - ETA: 0s - loss: 0.3336 - acc: 0.9067 15616/48000 [========>.....................] - ETA: 0s - loss: 0.3332 - acc: 0.9075 19072/48000 [==========>...................] - ETA: 0s - loss: 0.3305 - acc: 0.9085 22784/48000 [=============>................] - ETA: 0s - loss: 0.3264 - acc: 0.9095 26624/48000 [===============>..............] - ETA: 0s - loss: 0.3245 - acc: 0.9093 30464/48000 [==================>...........] - ETA: 0s - loss: 0.3263 - acc: 0.9085 34048/48000 [====================>.........] - ETA: 0s - loss: 0.3256 - acc: 0.9090 37760/48000 [======================>.......] - ETA: 0s - loss: 0.3271 - acc: 0.9092 40960/48000 [========================>.....] - ETA: 0s - loss: 0.3279 - acc: 0.9087 43648/48000 [==========================>...] - ETA: 0s - loss: 0.3285 - acc: 0.9084 46336/48000 [===========================>..] - ETA: 0s - loss: 0.3307 - acc: 0.9075 48000/48000 [==============================] - 1s 16us/step - loss: 0.3313 - acc: 0.9075 - val_loss: 0.3153 - val_acc: 0.9137
可以看出,在经过40轮迭代后,我们的网络在训练集上的多分类损失函数上下降到0.3313,在训练集上的准确率达到0.9075,在验证集上的多分类损失函数下降到0.3153,在验证集上的准确率达到0.9137,接着我们将测试集中的10000个样本输入训练好的模型进行性能评估;
#在测试集上对训练好的网络性能进行评估,返回第一项为损失函数,第二项为accuracy score = model.evaluate(X_test, Y_test, verbose=VERBOSE) #打印损失函数和准确率 print('Test Score:',score[0]) print('Test accuracy:',score[1])
2.4 添加隐层的多层感知机
上一个例子中我们使用不添加隐层的MLP在40轮迭代后达到0.9137的准确率,接下来我们来看看添加两层隐层后网络的学习能力会有怎样的提升,在keras中对MLP添加隐层的方法非常简单,只需要按照顺序在指定的位置插入隐层即对应的激活函数即可:
'''网络结构搭建部分''' #定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义网络中输入层与第一个隐层之间的部分 model.add(Dense(N_HIDDEN, input_shape=(RESHAPED,))) #为第一层隐层添加非线性激活函数 model.add(Activation('relu')) #添加第二层隐层 model.add(Dense(N_HIDDEN)) #为第二层隐层添加非线性激活函数 model.add(Activation('relu')) #定义输出层 model.add(Dense(NB_CLASSES)) #为输出层添加softmax激活函数 model.add(Activation('softmax')) #打印网络结构 model.summary()
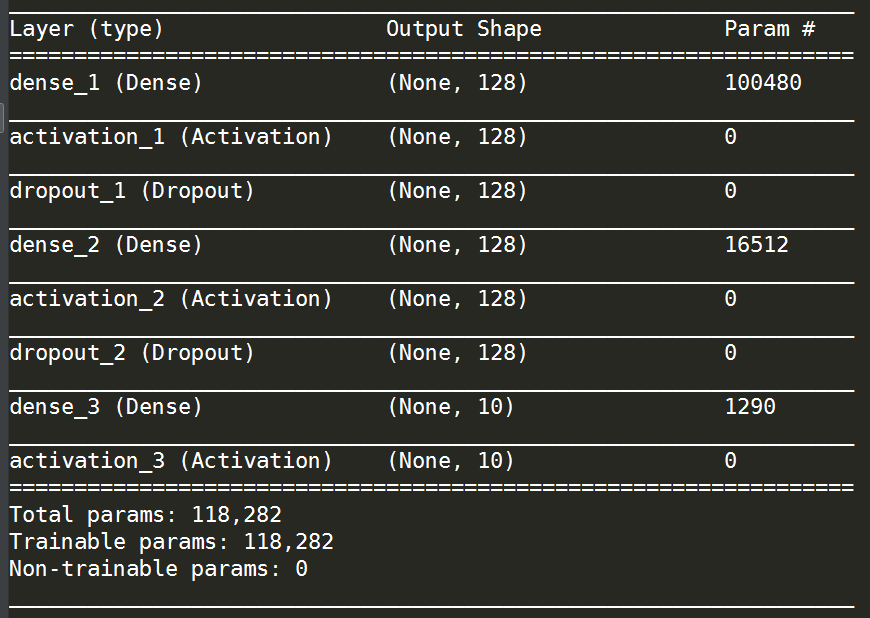
得到的新的网路结构如下:
其他部分代码均不变,得到40轮后的最终训练结果如下:
Epoch 40/40 128/48000 [..............................] - ETA: 1s - loss: 0.0715 - acc: 0.9922 1792/48000 [>.............................] - ETA: 1s - loss: 0.0997 - acc: 0.9721 3456/48000 [=>............................] - ETA: 1s - loss: 0.1142 - acc: 0.9702 4736/48000 [=>............................] - ETA: 1s - loss: 0.1157 - acc: 0.9704 6016/48000 [==>...........................] - ETA: 1s - loss: 0.1178 - acc: 0.9694 7424/48000 [===>..........................] - ETA: 1s - loss: 0.1141 - acc: 0.9698 8960/48000 [====>.........................] - ETA: 1s - loss: 0.1151 - acc: 0.9696 10624/48000 [=====>........................] - ETA: 1s - loss: 0.1165 - acc: 0.9697 12288/48000 [======>.......................] - ETA: 1s - loss: 0.1185 - acc: 0.9692 14080/48000 [=======>......................] - ETA: 1s - loss: 0.1162 - acc: 0.9695 15744/48000 [========>.....................] - ETA: 1s - loss: 0.1166 - acc: 0.9692 17408/48000 [=========>....................] - ETA: 0s - loss: 0.1178 - acc: 0.9682 19200/48000 [===========>..................] - ETA: 0s - loss: 0.1183 - acc: 0.9680 20864/48000 [============>.................] - ETA: 0s - loss: 0.1182 - acc: 0.9681 22528/48000 [=============>................] - ETA: 0s - loss: 0.1192 - acc: 0.9674 24192/48000 [==============>...............] - ETA: 0s - loss: 0.1192 - acc: 0.9675 25984/48000 [===============>..............] - ETA: 0s - loss: 0.1194 - acc: 0.9670 27648/48000 [================>.............] - ETA: 0s - loss: 0.1194 - acc: 0.9668 29312/48000 [=================>............] - ETA: 0s - loss: 0.1195 - acc: 0.9663 30976/48000 [==================>...........] - ETA: 0s - loss: 0.1202 - acc: 0.9658 32640/48000 [===================>..........] - ETA: 0s - loss: 0.1199 - acc: 0.9657 34304/48000 [====================>.........] - ETA: 0s - loss: 0.1202 - acc: 0.9659 35968/48000 [=====================>........] - ETA: 0s - loss: 0.1220 - acc: 0.9655 37632/48000 [======================>.......] - ETA: 0s - loss: 0.1224 - acc: 0.9654 39296/48000 [=======================>......] - ETA: 0s - loss: 0.1231 - acc: 0.9651 40960/48000 [========================>.....] - ETA: 0s - loss: 0.1226 - acc: 0.9651 42624/48000 [=========================>....] - ETA: 0s - loss: 0.1228 - acc: 0.9651 44288/48000 [==========================>...] - ETA: 0s - loss: 0.1223 - acc: 0.9652 45952/48000 [===========================>..] - ETA: 0s - loss: 0.1218 - acc: 0.9653 47744/48000 [============================>.] - ETA: 0s - loss: 0.1218 - acc: 0.9654 48000/48000 [==============================] - 2s 34us/step - loss: 0.1217 - acc: 0.9655 - val_loss: 0.1379 - val_acc: 0.9605
可以看出,网络性能在前面例子的基础上取得了显著的提升,下面再在测试集上评估网络性能得到结果如下:
2.5 添加Dropout层的双隐层MLP
Dropout是一种提升网络泛化能力的技巧,在我前面关于tensorflow的博客中也介绍过,它通过随机的将某一内部层的输出结果,抹除为0再传入下一层,达到提升网络泛化能力的效果,在keras中为MLP添加Dropout层非常方便:
from keras.layers.core import Dense,Dropout,Activation '''网络结构搭建部分''' ##定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义输入层与第一层隐层 model.add(Dense(N_HIDDEN, input_shape=(RESHAPED,))) #为第一层隐层添加非线性激活函数 model.add(Activation('relu')) #为第一层隐层的输出部分添加Dropout功能,即随机把指定比例的值修改为0 model.add(Dropout(0.3)) #定义第二层隐层 model.add(Dense(N_HIDDEN)) #为第二层隐层添加非线性激活函数 model.add(Activation('relu')) #为第二层隐层添加Dropout功能 model.add(Dropout(0.3)) #定义输出层 model.add(Dense(NB_CLASSES)) #为输出层定义softmax激活函数 model.add(Activation('softmax')) #打印模型结构信息 model.summary()
得到的新的网络结构如下:
同样在40轮训练后达到的性能效果如下:
Epoch 40/40 128/48000 [..............................] - ETA: 2s - loss: 0.2181 - acc: 0.9531 1536/48000 [..............................] - ETA: 1s - loss: 0.2049 - acc: 0.9414 2944/48000 [>.............................] - ETA: 1s - loss: 0.2062 - acc: 0.9385 4352/48000 [=>............................] - ETA: 1s - loss: 0.2032 - acc: 0.9391 5632/48000 [==>...........................] - ETA: 1s - loss: 0.2042 - acc: 0.9402 6912/48000 [===>..........................] - ETA: 1s - loss: 0.2010 - acc: 0.9423 8192/48000 [====>.........................] - ETA: 1s - loss: 0.1997 - acc: 0.9425 9600/48000 [=====>........................] - ETA: 1s - loss: 0.2016 - acc: 0.9426 11008/48000 [=====>........................] - ETA: 1s - loss: 0.2000 - acc: 0.9426 12288/48000 [======>.......................] - ETA: 1s - loss: 0.1998 - acc: 0.9427 13568/48000 [=======>......................] - ETA: 1s - loss: 0.1992 - acc: 0.9432 14848/48000 [========>.....................] - ETA: 1s - loss: 0.1969 - acc: 0.9438 16256/48000 [=========>....................] - ETA: 1s - loss: 0.1977 - acc: 0.9431 17408/48000 [=========>....................] - ETA: 1s - loss: 0.1999 - acc: 0.9425 18688/48000 [==========>...................] - ETA: 1s - loss: 0.2024 - acc: 0.9417 20096/48000 [===========>..................] - ETA: 1s - loss: 0.2029 - acc: 0.9412 21504/48000 [============>.................] - ETA: 1s - loss: 0.2034 - acc: 0.9406 22784/48000 [=============>................] - ETA: 0s - loss: 0.2027 - acc: 0.9406 24192/48000 [==============>...............] - ETA: 0s - loss: 0.2019 - acc: 0.9409 25600/48000 [===============>..............] - ETA: 0s - loss: 0.2015 - acc: 0.9413 27008/48000 [===============>..............] - ETA: 0s - loss: 0.2010 - acc: 0.9414 28288/48000 [================>.............] - ETA: 0s - loss: 0.2010 - acc: 0.9413 29696/48000 [=================>............] - ETA: 0s - loss: 0.1997 - acc: 0.9415 31104/48000 [==================>...........] - ETA: 0s - loss: 0.1999 - acc: 0.9408 32512/48000 [===================>..........] - ETA: 0s - loss: 0.2010 - acc: 0.9402 33792/48000 [====================>.........] - ETA: 0s - loss: 0.2025 - acc: 0.9401 35200/48000 [=====================>........] - ETA: 0s - loss: 0.2023 - acc: 0.9398 36608/48000 [=====================>........] - ETA: 0s - loss: 0.2020 - acc: 0.9399 38016/48000 [======================>.......] - ETA: 0s - loss: 0.2030 - acc: 0.9396 39296/48000 [=======================>......] - ETA: 0s - loss: 0.2025 - acc: 0.9398 40448/48000 [========================>.....] - ETA: 0s - loss: 0.2014 - acc: 0.9402 41472/48000 [========================>.....] - ETA: 0s - loss: 0.2017 - acc: 0.9400 42496/48000 [=========================>....] - ETA: 0s - loss: 0.2010 - acc: 0.9404 43520/48000 [==========================>...] - ETA: 0s - loss: 0.2024 - acc: 0.9401 44928/48000 [===========================>..] - ETA: 0s - loss: 0.2026 - acc: 0.9402 46336/48000 [===========================>..] - ETA: 0s - loss: 0.2026 - acc: 0.9403 47744/48000 [============================>.] - ETA: 0s - loss: 0.2033 - acc: 0.9401 48000/48000 [==============================] - 2s 43us/step - loss: 0.2036 - acc: 0.9401 - val_loss: 0.1375 - val_acc: 0.9618
在测试集上的评估效果如下:
三、完整代码
3.1 第一个不带隐层的多层感知机模型
'''这个脚本以MNIST手写数字识别为例演示无隐层的多层感知机模型在Keras中的应用''' import numpy as np from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.optimizers import SGD from keras.utils import np_utils '''设置随机数种子''' np.random.seed(42) '''网络结构参数预定义部分''' #定义训练轮数 NB_EPOCH = 40 #定义批尺寸 BATCH_SIZE = 128 #定义是否打印训练过程 VERBOSE = 1 #定义网络输出层神经元个数 NB_CLASSES = 10 #定义优化器 OPTIMIZER = SGD() #定义训练集中用作验证集的数据比例 VALIDATION_SPLIT = 0.2 '''数据预处理部分''' #因为keras中在线获取mnist数据集的方法在国内被ban,这里采用mnist.npz文件来从本地获取mnist数据 path = r'D:\anaconda\Lib\site-packages\keras\datasets\mnist.npz' with np.load(path) as f: X_train, y_train = f['x_train'], f['y_train'] X_test, y_test = f['x_test'], f['y_test'] #将格式为28X28的数据展开为1X784的结构以方便输入MLP中进行训练 RESHAPED = 784 '''将训练集与测试集重塑成维度为784,数值类型为float32的形式''' X_train = X_train.reshape(60000, RESHAPED).astype('float32') X_test = X_test.reshape(10000, RESHAPED).astype('float32') #归一化 X_train /= 255 X_test /= 255 #将类别训练目标向量转换为二值类别矩阵,即one-hot处理,传入单值,返回制定长度的向量表示形式 Y_train = np_utils.to_categorical(y_train, NB_CLASSES) Y_test = np_utils.to_categorical(y_test, NB_CLASSES) '''网络结构搭建部分''' #定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义输入层到输出层之间的网络部分 model.add(Dense(NB_CLASSES, input_shape=(RESHAPED,))) #为输出层添加softmax激活函数以实现多分类 model.add(Activation('softmax')) #打印模型结构 model.summary() #在keras中将上述简单语句定义的模型编译为tensorflow或theano中的模型形式 #这里定义了损失函数为多分类对数损失,优化器为之前定义的SGD随机梯度下降优化器,评分标准为accuracy准确率 model.compile(loss='categorical_crossentropy',optimizer=OPTIMIZER,metrics=['accuracy']) #进行训练并将模型训练历程及模型参数细节保存在history中,这里类似sklearn的方式,定义了自变量和因变量,以及批训练的尺寸,迭代次数,是否打印训练过程,验证集比例 history = model.fit(X_train ,Y_train, batch_size=BATCH_SIZE, epochs=NB_EPOCH,verbose=VERBOSE, validation_split=VALIDATION_SPLIT) #在测试集上对训练好的网络性能进行评估,返回第一项为损失函数,第二项为accuracy score = model.evaluate(X_test, Y_test, verbose=VERBOSE) #打印损失函数和准确率 print('Test Score:',score[0]) print('Test accuracy:',score[1])
3.2 添加隐层的多层感知机
'''这个脚本以MNIST手写数字识别为例演示带有隐层的基础多层感知机模型在Keras中的应用''' import numpy as np from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.optimizers import SGD from keras.utils import np_utils np.random.seed(42) '''网络结构参数预定义部分''' #定义训练轮数 NB_EPOCH = 40 #定义批尺寸 BATCH_SIZE = 128 #定义是否打印训练过程 VERBOSE = 1 #定义网络输出层神经元个数 NB_CLASSES = 10 #定义优化器 OPTIMIZER = SGD() #定义训练集中用作验证集的数据比例 VALIDATION_SPLIT = 0.2 #设置隐层神经元个数 N_HIDDEN = 128 '''数据预处理部分''' #因为keras中在线获取mnist数据集的方法在国内被ban,这里采用mnist.npz文件来从本地获取mnist数据 path = r'D:\anaconda\Lib\site-packages\keras\datasets\mnist.npz' with np.load(path) as f: X_train, y_train = f['x_train'], f['y_train'] X_test, y_test = f['x_test'], f['y_test'] #将格式为28X28的数据展开为1X784的结构以方便输入MLP中进行训练 RESHAPED = 784 X_train = X_train.reshape(60000, RESHAPED).astype('float32') X_test = X_test.reshape(10000, RESHAPED).astype('float32') #归一化 X_train /= 255 X_test /= 255 #将类别训练目标向量转换为二值类别矩阵 Y_train = np_utils.to_categorical(y_train, NB_CLASSES) Y_test = np_utils.to_categorical(y_test, NB_CLASSES) '''网络结构搭建部分''' #定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义网络中输入层与第一个隐层之间的部分 model.add(Dense(N_HIDDEN, input_shape=(RESHAPED,))) #为第一层隐层添加非线性激活函数 model.add(Activation('relu')) #添加第二层隐层 model.add(Dense(N_HIDDEN)) #为第二层隐层添加非线性激活函数 model.add(Activation('relu')) #定义输出层 model.add(Dense(NB_CLASSES)) #为输出层添加softmax激活函数 model.add(Activation('softmax')) #打印网络结构 model.summary() #编译模型 model.compile(loss='categorical_crossentropy',optimizer=OPTIMIZER,metrics=['accuracy']) #训练模型并保存训练过程细节信息 history = model.fit(X_train ,Y_train, batch_size=BATCH_SIZE, epochs=NB_EPOCH,verbose=VERBOSE, validation_split=VALIDATION_SPLIT) #在测试集上评估模型 score = model.evaluate(X_test, Y_test, verbose=VERBOSE) #打印损失函数及accuracy print('Test Score:',score[0]) print('Test accuracy:',score[1])
3.3 添加Dropout层的双隐层MLP
'''这个脚本以MNIST手写数字识别为例演示带有隐层的基础多层感知机模型在Keras中的应用''' import numpy as np from keras.models import Sequential from keras.layers.core import Dense,Dropout,Activation from keras.optimizers import SGD from keras.utils import np_utils np.random.seed(42) '''网络结构参数预定义部分''' #定义训练轮数 NB_EPOCH = 40 #定义批尺寸 BATCH_SIZE = 128 #定义是否打印训练过程 VERBOSE = 1 #定义网络输出层神经元个数 NB_CLASSES = 10 #定义优化器 OPTIMIZER = SGD() #定义训练集中用作验证集的数据比例 VALIDATION_SPLIT = 0.2 #设置隐层神经元个数 N_HIDDEN = 128 #设置Dropout的比例 DROPOUT = 0.3 '''数据预处理部分''' #因为keras中在线获取mnist数据集的方法在国内被ban,这里采用mnist.npz文件来从本地获取mnist数据 path = r'D:\anaconda\Lib\site-packages\keras\datasets\mnist.npz' with np.load(path) as f: X_train, y_train = f['x_train'], f['y_train'] X_test, y_test = f['x_test'], f['y_test'] #将格式为28X28的数据展开为1X784的结构以方便输入MLP中进行训练 RESHAPED = 784 X_train = X_train.reshape(60000, RESHAPED).astype('float32') X_test = X_test.reshape(10000, RESHAPED).astype('float32') #归一化 X_train /= 255 X_test /= 255 #将类别训练目标向量转换为二值类别矩阵 Y_train = np_utils.to_categorical(y_train, NB_CLASSES) Y_test = np_utils.to_categorical(y_test, NB_CLASSES) '''网络结构搭建部分''' ##定义模型为keras中的序贯模型,即一层一层堆栈网络层,以线性的方式向后传播 model = Sequential() #定义输入层与第一层隐层 model.add(Dense(N_HIDDEN, input_shape=(RESHAPED,))) #为第一层隐层添加非线性激活函数 model.add(Activation('relu')) #为第一层隐层的输出部分添加Dropout功能,即随机把指定比例的值修改为0 model.add(Dropout(0.3)) #定义第二层隐层 model.add(Dense(N_HIDDEN)) #为第二层隐层添加非线性激活函数 model.add(Activation('relu')) #为第二层隐层添加Dropout功能 model.add(Dropout(0.3)) #定义输出层 model.add(Dense(NB_CLASSES)) #为输出层定义softmax激活函数 model.add(Activation('softmax')) #打印模型结构信息 model.summary() #编译模型 model.compile(loss='categorical_crossentropy',optimizer=OPTIMIZER,metrics=['accuracy']) #训练模型并保存训练过程信息 history = model.fit(X_train ,Y_train, batch_size=BATCH_SIZE, epochs=NB_EPOCH,verbose=VERBOSE, validation_split=VALIDATION_SPLIT) #在测试集上评估模型 score = model.evaluate(X_test, Y_test, verbose=VERBOSE) #打印损失函数与准确率 print('Test Score:',score[0]) print('Test accuracy:',score[1])
以上就是本文的全部内容,如有笔误,望指出。
参考文献:Keras深度学习实战