继续图形学之旅,我们已经解决了如何画线和画圆的问题,接下来要解决的是,如何往一个区域内填充颜色?对一个像素填充颜色只需调用SetPixel之类的函数就行了,所以这个问题其实就是:如何找到一个区域内的所有像素?
区域的表示方法
定义一个区域可以有两种方法,即内点表示法和边界表示法,内点表示就是指用一种颜色表示区域内的点,只要当前像素是这种颜色就在区域内,边界表示就是用一种颜色表示区域边界,只要当前像素是这种颜色就表示到达了区域边界。
简单的种子填充算法
最简单暴力的填充算法即是从区域内一点出发,向四周扩散填充,到达区域边界时停止,常见的有四邻法和八邻法两种,顾名思义,一个是向上下左右四个方向扩散填充,另一个是向周围八个方向扩散,四邻法可以确保不溢出区域边界,但有可能出现一次填不满区域的情况,八邻法则相反,一定能填充满当前区域,但有从对角线溢出边界的危险。
边界表示的四邻法代码实现:
void BoundaryFill4(HDC hdc, int x, int y, COLORREF boundaryColor, COLORREF newColor)
{
COLORREF c = GetPixel(hdc, x, y);
if (c != newColor && c != boundaryColor)
{
SetPixel(hdc, x, y, newColor);
BoundaryFill4(hdc, x + 1, y, boundaryColor, newColor);
BoundaryFill4(hdc, x - 1, y, boundaryColor, newColor);
BoundaryFill4(hdc, x, y + 1, boundaryColor, newColor);
BoundaryFill4(hdc, x, y - 1, boundaryColor, newColor);
}
}我们用之前学习的Bresenham画线算法画一个矩形,然后用这个算法填充它。
Bresenham_Line(150, 150, 150, 200, hdc, RGB(0, 0, 0));
Bresenham_Line(150, 200, 200, 200, hdc, RGB(0, 0, 0));
Bresenham_Line(200, 200, 200, 150, hdc, RGB(0, 0, 0));
Bresenham_Line(200, 150, 150, 150, hdc, RGB(0, 0, 0));
BoundaryFill4(hdc, 175, 175, RGB(0, 0, 0), RGB(255, 0, 0));运行效果:
很显然,这种递归的填充算法简单好理解,但效率是不可接受的,实际上我运行时填充100*100像素的区域就直接GG了(堆栈溢出),显然我们需要提高算法效率,避免过多的递归调用。
扫描线种子填充算法
为了提高效率可以使用扫描线种子填充算法,这里的扫描线就是与x轴相平行的线,该算法可以由以下4个步骤实现:
- 初始化:堆栈置空,将初始种子点(x,y)入栈
- 出栈:若栈空则算法结束,否则取栈顶元素(x,y),以y作为当前扫描线
- 填充并确定种子点所在区段:从种子点(x,y)出发,向左右两个方向填充,直到边界。标记区段左右断点为xl和xr。
- 确定新的种子点:在区间[xl,xr]中检查与当前扫描线y上下相邻的两条扫描线上的像素。若存在非边界、未填充像素,则把每一区间最右像素作为种子点压入堆栈,返回第二步。
代码实现:
void ScanLineFill4(HDC hdc, int x, int y, COLORREF oldColor, COLORREF newColor)
{
int xl, xr;
bool SpanNeedFill;
pair seed;
stack> St;
seed.first = x; seed.second = y;
St.push(seed);
while (!St.empty())
{
seed = St.top();
St.pop();
y = seed.second;
x = seed.first;
while (GetPixel(hdc,x,y) == oldColor)//向右填充
{
SetPixel(hdc, x, y, newColor);
x++;
}
xr = x - 1;
x = seed.first - 1;
while (GetPixel(hdc, x, y) == oldColor)//向左填充
{
SetPixel(hdc, x, y, newColor);
x--;
}
xl = x + 1;
//处理上方的一条扫描线
x = xl;
y = y + 1;
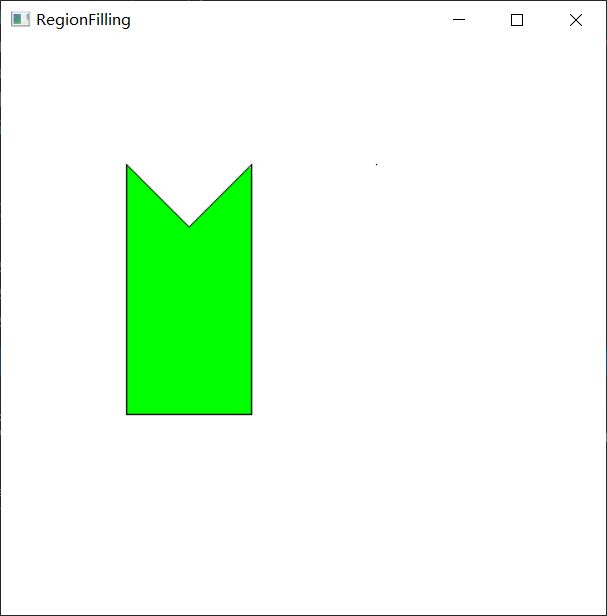
while (x 这次画一个不太规则的图形试试吧。
Bresenham_Line(100, 100, 150, 150, hdc, RGB(0, 0, 0));
Bresenham_Line(150, 150, 200, 100, hdc, RGB(0, 0, 0));
Bresenham_Line(200, 100, 200, 300, hdc, RGB(0, 0, 0));
Bresenham_Line(200, 300, 100, 300, hdc, RGB(0, 0, 0));
Bresenham_Line(100, 300, 100, 100, hdc, RGB(0, 0, 0));
ScanLineFill4(hdc, 150, 175, RGB(255, 255, 255), RGB(0, 255, 0));这次由于对每一个待填充区段只需要压栈一次,所以效率提高了,也没有堆栈溢出的危险,但说实话上面的填充进行了接近十秒钟才完成,如果画图软件使用这种填充算法估计是没人会用了吧......
有序边表的扫描线算法
接下来是最复杂的一种的扫描线算法,需要多边形的所有边信息,主要思想是求得每一条扫描线与多边形的交点,从而两两配对得到处在多边形内的区间,对这些区间进行上色,但要求扫描线与多边形的交点,直接暴力地遍历每条边肯定是不可行的,我们需要引入活性边表AET和新边表NET来辅助计算。
NET中存放的是在该扫描线第一次出现的边,也就是最低端点的y值等于当前扫描线位置的边,对每一个结点,需要存储当前x值、直线斜率倒数和直线最高点y值,如下图所示:
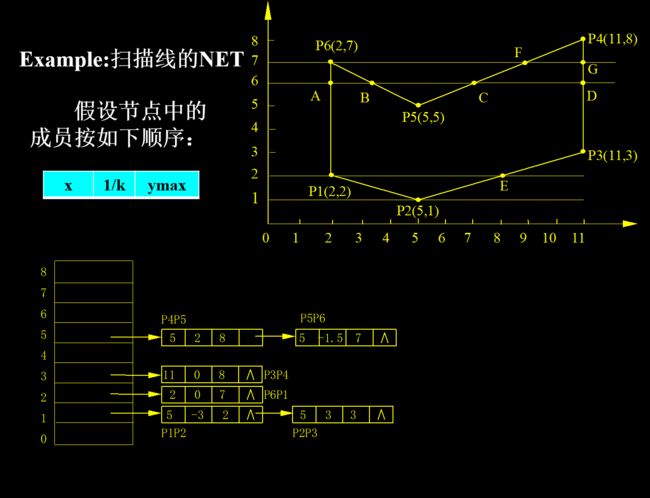
通过NET就可以容易地得到AET,AET中存放的是扫描线与多边形的交点。我们从下往上遍历每条扫描线,对于扫描线i来说,将NET[i]中结点插入,将AET[i-1]中ymax=i的结点删除,其余结点将x值加上斜率倒数之后插入,就得到了AET[i]。
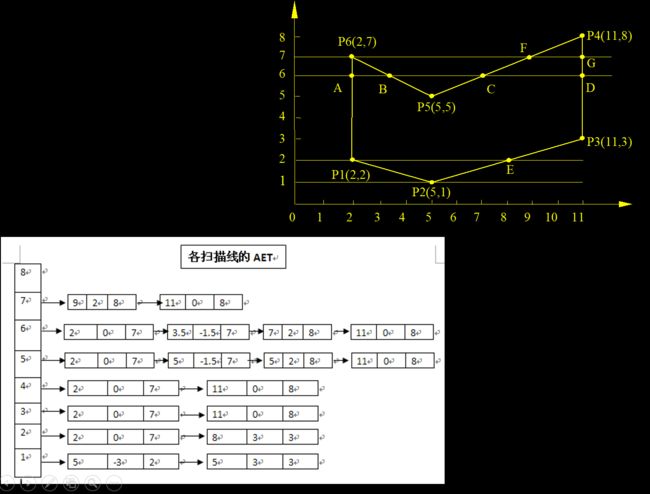
有了AET之后,只需要配对每两个交点,把区间内像素上色就可以了,但要注意,由于要从左到右配对,所以
AET表应时刻保持按x坐标递增排序。
伪代码:
void PolyFill(polygon,color)
{
初始化新边表NET和活性边表AET;
for(每条扫描线i)
{
把ymin=i的边放进边表NET[i];
}
for(每条扫描线i)
{
把新边表NET[i]中结点插入AET[i](x坐标递增有序排列);
AET[i-1]中ymax!=i的结点加入AET[i];
遍历AET[i],把配对交点区间中像素上色;
}
}边界标志算法
还有一种基于扫描线思想的边界标志算法,比较适合用硬件实现。基本思想是对多边形每条边进行扫描转换,找到多边形边界的所有像素,对每条与多边形相交的扫描线按从左到右的顺序扫描每个像素,用一个布尔值inside表示当前点是否在多边形内(初始为false),只要扫描到多边形边界像素,就把inside取反,若inside为真,则表示该点在多边形内,则填充该像素。
伪代码:
void edgemark_fill(polydef,color)
{
对多边形每条边扫描转换;
inside=false;
for(每条扫描线)
{
for(扫描线上每个像素)
{
if(该像素是边界像素)
inside=!inside;
else if(inside==true)
SetPixel(x,y,color);
}
}
}