JS刷算法题：二叉树

Q1.翻转二叉树（easy）

如题所示

示例：

输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/invert-binary-tree

 

这道题目起源于一个非常搞笑的事件：据说大名鼎鼎的Mac软件包管理工具Homebrew的作者，因为做不出这道在leetcode上难度为easy的题，被谷歌公司拒了。。。

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

如何看待 Max Howell 被 Google 拒绝？​www.zhihu.com

 

格式要求

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
  // 编码
};

 

分析：二叉树遍历

思路就是遍历二叉树的每一个节点，然后把左右链接替换一下就可以了。前序/中序/后序 都可以。如下所示

 

具体代码

var invertTree = function(root) {
  traveral(root);
  return root;
};

function traveral(node) {
  if (node === null) return;
  traveral(node.left);
  traveral(node.right);
  const temp = node.right;
  node.right = node.left;
  node.left = temp;
}

 

 

Q2.二叉树的右视图(middle)

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

   1            <---
 /   \
2     3         <---
 \     \
  5     4       <---

输入: [1,2,3,null,5,null,null]
输出: [1, 3, 5]
解释:
   1            <---
 /   \
2     3         <---
 \     
  5             <---

来源：LeetCode
链接：https://leetcode-cn.com/problems/binary-tree-right-side-view

 

格式要求

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function(root) {
 // 编码
}

 

分析：层序遍历

题目的思路很明显，对二叉树进行层序遍历，然后取得每一层的最后一个节点。放到一个数组里最后返回。

1.我们可以设置一个队列存放依次遍历的节点对象。

2.使用两层循环

• 内层循环通过不断出队列的方式遍历当前层的节点，同时通过左右链接收集下一层节点

• 外层循环判断队列长度>0时就继续运行，从而实现逐层迭代

3.在每次内层循环中获取最右端的非空节点

 

具体代码

var rightSideView = function(root) {
  if (!root) return [];
  const queue = [];
  const arrRS = [];
  // 先保存根结点，也就是第一层二叉树
  queue.push(root);
  while (queue.length > 0) {
    // 将队列长度先保存到一个变量里面
    // 表示的是上一层的节点的数量
    let length = queue.length;
    let temp = null;
    // 遍历上一层节点，将它们的子节点加入队列中，收集得到二叉树的下一层
    for (let i = 0; i < length; i++) {
      // 出队列，并获得返回的父节点
      const node = queue.shift();
      // 每次都用当前节点的val覆盖temp
      // temp最后会等于当前层最右的一个非空节点的val值
      if (node.val) temp = node.val;
      // 收集当前节点的左节点和右节点，从而得到下一层
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    // 收集每一层的最右节点
    arrRS.push(temp);
  }
  return arrRS;
};

 

Q3.二叉树中的最大路径和(difficult)

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例1:
输入: [1,2,3]

       1
      / \
     2   3

输出: 6

示例2:
输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

来源：LeetCode
链接：https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/

 

格式要求

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function(root) {
  // 编码
};

 

思路分析

1.整体思路：通过后序遍历，自底向上计算。

因为后序遍历的计算过程是：左节点-右节点-根结点。 所以通过这种遍历方式，我们可以在计算两个子节点的基础上，推断当这两个节点到父节点的最大路径和。然后不断向上累加，去计算最大值。

同时在每个节点都通过Math.max更新当前的最大值，直到回归到根结点的时候，也就能比较出最大值来了。

 

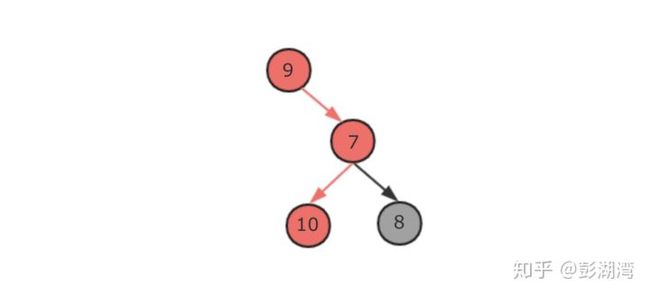
2.路径的单一性： 当一个节点是只是作为一个中间节点，而不是一个根节点的时候：左节点和右节点只能选择一个作为经过的路径。 因为路径是“单一”的而不是“分叉”的

例如下面的图示中， 当我们通过比较选择9-7-10这条的时候，节点8就不在路径内了

 

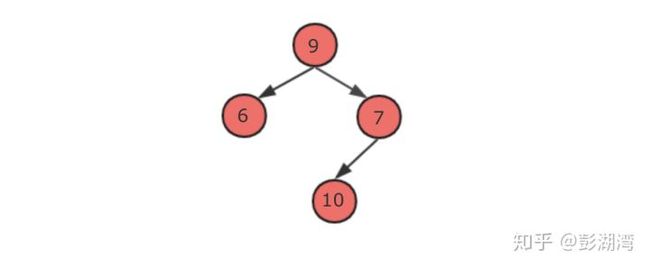
3.根节点的连接性：当一个节点作为根节点的时候，它可以将两个子树的路径连接起来

 

4. 对于两个子节点的累加值A，B，分3种情况讨论

• A>0,B>0: 选择Math.max(A,B)作为经过路径

• A>0,B<0: 选择A作为经过路径

• A<0,B>0: 选择B作为经过路径

• A<0,B<0: A,B都不选

 

综上所述

我们的思路是：

1. 后序遍历，自底向上计算

2. 对于每个节点，假设它是根结点，计算它联合两个子树路径后的最大值

3. 对于每个节点，假设它是中间节点，选择两条中较大的一条子树作为路径

4. 对于2，3分上面的四种情况进行分别处理

 

具体代码

// 1.考虑全为负数的情况
// 2.考虑当前节点为负的情况
let max = Number.MIN_VALUE;
var maxPathSum = function(root) {
  max = root.val;
  traveral(root);
  return max;
};

function traveral(node) {
  if (node === null) return 0;
  const a = traveral(node.left);
  const b = traveral(node.right);
  let v = node.val;
  if (a >= 0 && b >= 0) {
    max = Math.max(max, v + a + b);
    v += Math.max(a, b);
  } else if (a >= 0) {
    max = Math.max(max, v + a);
    v += a;
  } else if (b >= 0) {
    max = Math.max(max, v + b);
    v += b;
  }
  return v;
}

function TreeNode(val) {
  this.val = val;
  this.left = this.right = null;
}

 

本文完