C:子段乘积
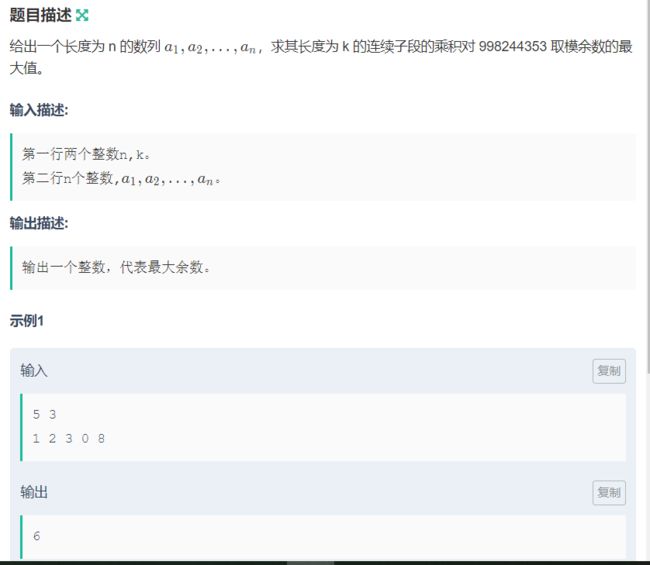
考察点 : 线段树,尺取,乘法逆元
坑点 : 区间要做到不重不漏, long long
侃侃 :
这道题在比赛是写的尺取,但是写了半天发现不好处理除 0 问题(浮点错误),需要用到乘法逆元(就是把除法转换成乘法的
的过程,应该是用到费马小定理),由于这块不太会,就不会搞了。之后看到题解说用线段树才反应过来,确实呀,这明显就是
区间问题,而且线段树的时间复杂度是 logN,完全可以呀,而且也不用处理除 0 问题(因为我们区间里面每个元素都是 乘)
哈哈,还是自己运用的知识不够灵活吧,不过有了这次的体验之后遇到区间问题应该会多往这个角度考虑一下。
线段树不太了解请点击(专为像我一样的萌新准备)
Code:
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 2e5 + 10;
const int mod = 998244353;
typedef long long LL;
struct node {
int l,r;
LL sum;
}tr[maxn << 2];
int a[maxn];
int n,k;
int main(void) {
void build(int u,int l,int r);
LL query(int u,int l,int r);
scanf("%d%d",&n,&k);
for(int i = 1; i <= n; i ++) {
scanf("%d",&a[i]);
}
build(1,1,n);
LL ans = 0;
for(int i = 1; i <= n - k; i ++) {
// 每次的长度是 k ,做到不重不漏
ans = max(ans,query(1,i,i + k - 1) % mod);
}
cout << ans % mod << endl;
return 0;
}
void pushup(int u) {
tr[u].sum = (tr[u << 1].sum % mod * tr[u << 1 | 1].sum % mod) % mod;
return ;
}
void build(int u,int l,int r) {
tr[u].l = l,tr[u].r = r;
if(l == r) {
tr[u].sum = a[l] % mod;
return ;
}
int mid = l + r >> 1;
build(u << 1,l,mid);
build(u << 1 | 1,mid + 1,r);
pushup(u);
return ;
}
LL query(int u,int l,int r) {
if(tr[u].l >= l && tr[u].r <= r) {
return tr[u].sum % mod;
}
int mid = tr[u].l + tr[u].r >> 1;
LL sum = 1;
if(l <= mid) sum = query(u << 1,l,r) % mod;
if(r > mid) sum = (sum % mod * query(u << 1 | 1,l,r) % mod ) % mod;
//只是将原来的求和换成乘积就可以了
return sum % mod;
}
