本文由 伯乐在线 - Janzou 翻译,之似 校稿。未经许可,禁止转载!
英文出处:theory.stanford.edu。欢迎加入翻译组。
本系列:
- 关于寻路算法的一些思考(1):A* 算法介绍
- 关于寻路算法的一些思考(2):Heuristics 函数
- 关于寻路算法的一些思考(3):A* 算法的实现
- 关于寻路算法的一些思考(4):A* 算法的变体
- 关于寻路算法的一些思考(5):处理移动中的障碍物
- 关于寻路算法的一些思考(6):预先计算好的路径的所用空间
- 关于寻路算法的一些思考(7):地图表示
- 关于寻路算法的一些思考(8):长期和短期目标
- 关于寻路算法的一些思考(9):寻路者的移动成本
- 关于寻路算法的一些思考(10):最短路径的用户体验
- 关于寻路算法的一些思考(11):寻路算法的其他应用
- 关于寻路算法的一些思考(12):AI 技术
启发式函数h(n)告诉A*从任何结点n到目标结点的最小代价评估值。因此选择一个好的启发式函数很重要。
启发式函数在A* 中的作用
启发式函数可以用来控制A*的行为。
- 一种极端情况,如果h(n)是0,则只有g(n)起作用,此时A* 算法演变成Dijkstra算法,就能保证找到最短路径。
- 如果h(n)总是比从n移动到目标的代价小(或相等),那么A* 保证能找到一条最短路径。h(n)越小,A* 需要扩展的点越多,运行速度越慢。
- 如果h(n)正好等于从n移动到目标的代价,那么A* 将只遵循最佳路径而不会扩展到其他任何结点,能够运行地很快。尽管这不可能在所有情况下发生,但你仍可以在某些特殊情况下让h(n)正好等于实际代价值。只要所给的信息完善,A* 将运行得很完美。
- 如果h(n)比从n移动到目标的代价高,则A* 不能保证找到一条最短路径,但它可以运行得更快。
- 另一种极端情况,如果h(n)比g(n)大很多,则只有h(n)起作用,同时A* 算法演变成贪婪最佳优先搜索算法(Greedy Best-First-Search)。
所以h(n)的选择成了一个有趣的情况,它取决于我们想要A* 算法中获得什么结果。h(n)合适的时候,我们会非常快速地得到最短路径。如果h(n)估计的代价太低,我们仍会得到最短路径,但运行速度会减慢。如果估计的代价太高,我们就放弃最短路径,但A* 将运行得更快。
在游戏开发中,A* 的这个特性非常有用。例如,你可能会发现在某些情况下,你宁愿有一个“好”的路径而不是一个“完美”的路径。为了平衡g(n)和h(n)之间的关系,你可以修改其中的任何一个。
注释: 从技术上来看,如果启发式函数值低估了实际代价,A* 算法应该被称为简单的A算法(simply A)。不过,我将继续称之为A* 算法,因为它们的实现是相同的,而且游戏编程社区对A算法和A* 算法并不区分对待。
速度和准确性?
A* 基于启发式函数和代价函数来改变其行为的能力在游戏中非常有用。速度和准确性之间的折衷可以提高游戏速度。对于大多数游戏而言,你并不需要两个点之间的最佳路径。你只需要知道近似的路径就足够了。你所需要的路径往往取决于游戏中接下来要发生什么,或是运行游戏的计算机有多快。
假设你的游戏中有两种地形,平原和山地,它们的移动代价分别是1和3,A* 算法沿着平原搜索的路径长度是沿着山区的三倍。这是因为可能有一条绕着山地的平原路径。你可以把两个地图单位之间的启发式距离设为1.5可以加快A* 的搜索速度。于是A* 会将山区的移动成本3改为1.5,这个变化不像3到1那么大。这种方法在山区的移动成本不像之前那样高,因此不用花太多的时间去寻找绕着山地的路径。或者,你可以通过告诉A* 在山区的移动成本为2而不是3,以减少山区周围路径的搜索量,来加快A* 的搜索速度。现在,沿着平原搜索路径的速度只是沿着山区的两倍。这两种方法都放弃了理想路径来获得更快的搜索速度。
速度和准确性之间的权衡不需要是固定的。你可以根据CPU速率、用于寻路的时间片数、地图上物体的数量、物体的重要性、组(group)的大小、难度级别,或其他任何因素来进行动态地选择。一种动态的折衷启发式函数方法是,假设通过一个网格空间的最小代价为1,然后建立一个在下式中范围内的代价函数(cost function):
g'(n) = 1 + alpha * (g(n) - 1)
如果alpha值为0,则修改后后的代价函数的值将总是为1。在这种情况下,地形代价被完全忽略,A* 的工作变成了简单判断一个网格能否通过。如果alpha的值为1,则初始代价函数将被使用,你会得到A* 算法的所有优点。你可以将alpha设为0到1之间的任意值。
你也应该考虑在启发式函数返回的绝对最小代价和期望最小代价中做选择。例如,如果你的地图上大部分地形是移动代价为2的草地而一些地形是移动代价为1的道路,那么你可以考虑让启发式函数假设没有道路,而只返回两倍的距离。
速度和准确性之间的选择并不必是全局的。在地图上的某些区域,你可以基于其准确性的重要性来进行动态选择。举个例子,假设我们在任意点都可能停止并重新计算路径或改变方向,那么为什么要困扰于后续路径的准确性呢?在这种情况下快速选择一条的路径更加重要。或者,对于地图上的某个安全区域,准确的最短路径并不那么重要;但在渡过危险区域时,安全和准确是必需的。
度量
A* 计算f(n) = g(n) + h(n)。为了将两个值相加,这两个值必须使用相同的单位去度量。如果度量g(n)的单位是小时,衡量h(n)的单位是米,则A* 将认为g或h太大或太小,因此,要么你无法得到好的路径,要么A* 的运行速度会更慢。
精确启发式函数
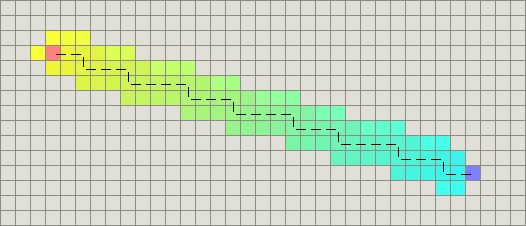
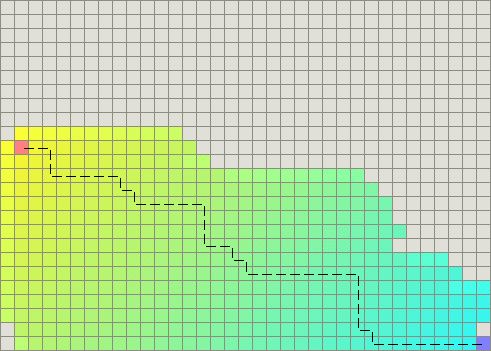
如果你的启发式函数值正好等于最佳路径的距离,正如下一部分的图中所示,你会看到A* 扩展的结点非常少。A* 算法所做的是在每个结点处计算f(n) = g(n) + h(n)。当h(n)和g(n)完全匹配时,f(n)的值不会沿着路径改变。不在正确路径上的所有结点的f值均大于正确路径上结点的f值。由于A* 在考虑f值较低的点前,不会考虑f值较高的点,因此它肯定不会偏离最短路径。
预先计算的精确启发式函数
构造精确的启发式函数的一种方法是预先计算每对结点之间的最短路径的长度。这种做法对于大多数游戏的地图而言并不可行。但是,有几种方法可以近似模拟启发式函数:
- 在细网格(fine grid)拟合合适密度的粗网格(coarse grid)。 预先计算粗网格中任何一对结点之间的最短路径。
- 预先计算任何一对路径点(waypoints)之间的最短路径。这是粗网格方法的一般化。
然后添加一个启发式函数h’来估计从任何位置到其邻近路径点的代价。(如果需要,后者也可以通过预计算得到。)最终的启发式函数将是:
h(n) = h'(n, w1) + distance(w1, w2) + h'(w2, goal)
或者,如果你想要一个更好但代价更大的启发式函数,则分别用靠近结点和靠近目标的所有w1, w2对上式进行计算。
线性的精确启发式函数
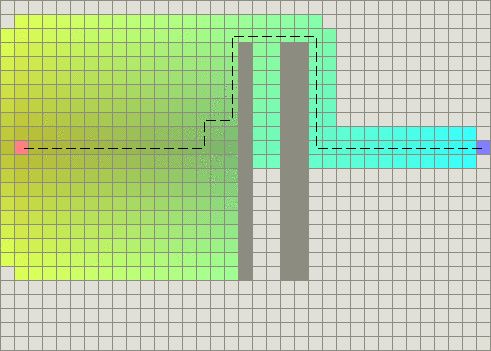
在特殊情况下,不需要预先计算也能使启发式函数很精确。如果你的地图没有障碍物或者移动缓慢的区域,那么从初始点到目标点的最短路径应该是一条直线。
如果你使用的是简单的启发式函数(不知道地图上障碍物的情况),那么它应该匹配精确的启发式函数。如果没有,那么你选择的启发式函数的类型和衡量单位可能有问题。
网格地图中的启发式函数
在网格地图中,有一些众所周知的启发式函数可供使用。
启发式函数的距离与所允许的移动方式相匹配
- 在正方形网格中,允许向4邻域的移动,使用曼哈顿距离(L1)。
- 在正方形网格中,允许向8邻域的移动,使用对角线距离(L∞)。
- 在正方形网格中,允许任何方向的移动,欧几里得距离(L2)可能适合,但也可能不适合。如果用A* 在网格上寻找路径,但你又不允许在网格上移动,你可能要考虑用其它形式表现该地图。
- 在六边形网格中,允许6个方向的移动,使用适合于六边形网格的曼哈顿距离。
曼哈顿距离(Manhattan distance)
对于方形网格,标准的启发式函数就是曼哈顿距离。考虑一下你的代价函数并确定从一个位置移动到相邻位置的最小代价D。在简单的情况下,你可以将D设为1。在一个可以向4个方向移动的方向网格中,启发式函数是曼哈顿距离的D倍:
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
return D * (dx + dy)
如何确定D?你使用的衡量单位应该与你的代价函数相匹配。对于最佳路径,和“可采纳的”的启发式函数,应该将D设为邻近方格间移动的最低代价值。在一个没有障碍物、最小移动代价为D的地形上,每向目标靠近移动一步,g就增加D的移动代价同时h减少D的代价。此时将g和h相加时,f保持不变;这是启发式函数与代价函数的衡量单位相匹配的一个标识。你也可以通过放弃最优路径增加代价D或是降低最低和最高边际代价之间比率的手段,来让A* 的运行速度更快。
(注:上述图像的启发式函数中加入了 决胜值(tie-breaker)
对角线距离
如果你允许在地图中沿着对角线移动,那么你需要一个不同的启发式函数(有时被称为契比雪夫距离(Chebyshev distance))。偏东4个单位偏北4各单位(4 east, 4 north)的曼哈顿距离是8*D。然而,对对角线距离而言,你可以简单地移动4个对角线长度,因此启发式函数将为4*D。下面这个函数用于处理对角线,假设直线和对角线的移动代价都是D:
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
return D * max(dx, dy)
如果你沿对角线移动的代价并不是D,而是类似于D2 = sqrt(2)*D,那么上面的启发式函数并不适合你。你会想要一个更复杂而准确的函数:
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)
在这里,我们计算不走对角线所需要的步数,然后减去走对角线节约的步数。在对角线上的步数有min(dx, dy)个,其每步的代价为D2,可以节约2*D的非对角线步数的代价。
Patrick Lester用一种不同的方式来写这个启发式函数,他使用dx > dy及dx < dy显式的表达。上面的代码有相同的测试方法,但它隐藏了内部对min函数的调用。
欧几里得距离
如果你允许沿着任何角度移动(而不是网格方向),那么你或许应该使用直线距离:
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
return D * sqrt(dx * dx + dy * dy)
然而,在这种情况下,你直接使用A* 将可能有麻烦,因为代价函数g不会匹配启发式函数h。由于欧几里得距离比曼哈顿距离或对角线距离更短,你仍然会得到最短路径,但A* 将需要更长的运行时间:
平方后的欧几里得距离
我曾看到一些有关A* 的网页推荐你使用距离的平方来避免欧几里得距离中耗时的平方根计算。
|
1
2
3
4
|
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
return D * (dx * dx + dy * dy)
|
千万不要这样做!这无疑会导致衡量单位的问题。因为你要将函数g和h的值相加,它们的衡量单位需要相匹配。当A* 计算f(n) = g(n) + h(n)时,距离的平方将比函数g的代价大很多,并且你会因为启发式函数的评估值过高而停止。对于较长的距离,这样做会接近g(n)的极端情况而对计算f(n)没有任何帮助,A* 算法将退化成贪婪最佳优先搜索算法(Greedy Best-First-Search):
你也可以缩小启发式函数的度量单位。然而,此时你会面临相反的问题:对于较短的距离,相比于g(n),启发式函数的代价将小得多,A* 算法将退化成Dijkstra算法。
如果你经过分析发现平方根的代价很显著,要么使用快速平方根逼近欧几里得距离,要么使用对角线距离作为欧几里得距离的近似值。
多个目标
如果你想要搜索几个目标中的一个,构建一个启发式函数h'(x),它是h1(x), h2(x), h3(x), …中最小的,其中h1, h2, h3是每个目标点附近的启发式函数。
如果你想要搜索一个目标附近的点,要求A* 算法找到一条路径通往目标区域的中心。当处理的节点来自开放集(OPEN set)时,在得到一个足够近的节点时退出。
值相等时的决胜法(Breaking ties)
在一些网格地图上,有许多具有相同的长度的路径。例如,在没有变化的地形平坦的区域中,使用网格会产生许多等长的路径。A* 可能会搜索具有相同f值的所有路径,而不是其中一条。
f值的相等情况
为了解决这个问题,我们需要调整g或h的值;调整h的值通常会更容易。决胜值(tie breaker)必须根据顶点来确定(即,它不应该仅是一个随机数),而且它必须使f值不同。因为A* 对f值排序,让f值不同意味着所有“等价”的f值中只有一个将被搜索到。
在相等的值中进行抉择的一种方式是稍微改变(nudge)h值的衡量单位。如果减小衡量单位,那么当我们朝着目标点移动时,f值将逐渐增加。不幸的是,这意味着A* 将更倾向于扩展靠近初始点的结点,而不是靠近目标点的结点。我们可以稍微增大衡量单位(甚至是0.1%)。A* 将更倾向于扩展靠近目标点的结点。
heuristic *= (1.0 + p)
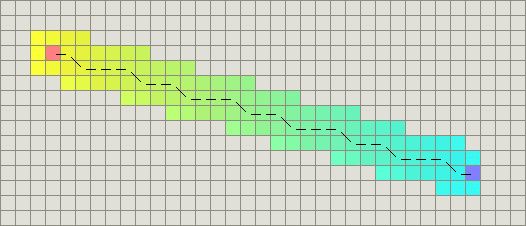
因子p的选择应该使得p<(移动一步的最小代价)/(期望的最长路径长度)。假设你不希望路径超过1000步,你可以使p = 1/1000。(注意,这稍微打破了“可受理”启发式函数,但在游戏中几乎从来不重要。)改变这个关键值(tie-breaking)的结果使A* 在地图上搜索的结点比以前更少:
加入比例决胜值后的启发式函数。
当有障碍物时,仍然要在其周围寻找路径,但要注意在绕过障碍物之后,A* 搜索的区域非常少:
加入比例型决胜值的启发式函数在在有障碍物时也能得到较好的效果。
Steven van Dijk建议,一个更直截了当的方法是把h作为比较函数的依据。当f值相等时,比较函数将通过检查h来解决f值相等的情况。
另一种方法是添加一个确定的随机数到启发式函数或边的代价(选择确定的随机数的一种方法是计算坐标的哈希值。)这比上面提到的调整h值能更好的解决f值相等的问题。感谢Cris Fuhrman的这个建议。
另一种的方法更倾向于沿着从起始点到目标点的直线路径:
dx1 = current.x - goal.x
dy1 = current.y - goal.y
dx2 = start.x - goal.x
dy2 = start.y - goal.y
cross = abs(dx1*dy2 - dx2*dy1)
heuristic += cross*0.001
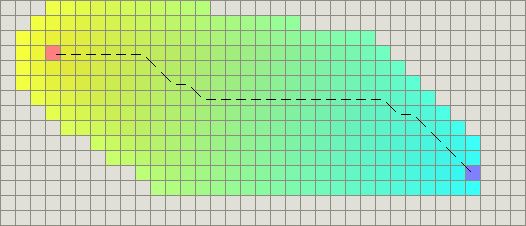
这段代码计算初始-目标向量和当前-目标向量之间的向量叉积。当这些向量不平行时,叉积将很大。其结果是,这段代码选择的路径稍微倾向于沿着初始点到目标点的直线路径。当没有障碍物时,A* 不仅搜索很少的区域,而且它找到的路径看起来非常好:
启发式函数中加入叉积作为决胜值,产生更好的路径。
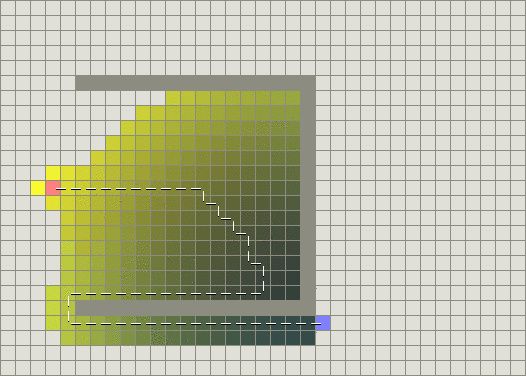
但是,因为这个决胜值更倾向于从初始点到目标点的直线路径,当出现障碍物时会出现奇怪的结果(请注意,这条路径仍然是最佳的;它只是看起来很奇怪):
启发式函数中加入叉积作为决胜值,在有障碍物时效果不够好。
为了交互式地探索这种关键值方法的改进,请参考James Macgill的A* 应用?[或使用这个镜像或这个镜像]。使用”Clear”来清除地图,并选择地图上对角的两个点。当你使用“Classic A*”方法时,你会看到关键值的效果。当你使用“Fudge”方法时,你会看到上面提到给启发式函数添加叉积后的效果。
另一种方法是小心地构造你的A* 优先队列,使新插入的特定f值的结点总是比那些具有相同f值的旧结点有更高的优先级。
同时,另一种在网格上打破平局的方法是尽量减少转向。从上一结点到当前结点x,y的变化将告诉你你的移动方向。对于所有当前点到下一相邻点构成的边而言,如果x,y的移动方向与从上一结点到当前结点的移动方向不同,那么在移动代价中增加一个小的惩罚值。
如果多个相等的f值出现次数很多,上述对启发式函数的修改可能仅仅是一个“创口贴”般的低效方法。当有大量一样好的路径时,多个相等f值的出现会导致大量结点被搜索。考虑“更聪明而不是更辛苦”的方法:
- 替换地图表征可以通过减少图形上结点的数量来解决这个问题。将多个结点归于一个,或删除重要结点外的所有结点。长方形对称缩减(Rectangular Symmetry Reduction)是在方形网格上实现这个的一个办法;同时还可以考虑“framed quad trees”方法。分层寻路(Hierarchical pathfinding)使用具有少量结点的高层级图形来找到最佳路径,然后使用具有大量结点的低层级图形完善该路径。
- 某些方法让大量结点独立但减少了被访问结点的数量。?Jump Point 搜索跳过大面积含有大量关系的结点;该方法被设计用于方形网格。跳过链接添加“捷径”的边来跳过地图上的区域。AlphA* 算法添加了一些深度优先搜索到A* 通常的广度优先的行为中,以便它可以探索单条路径而不是同时处理所有这些路径。
- Fringe 搜索(PDF)?通过结点快速处理来解决这个问题。它分批处理结点,只扩展具有低f值的结点,而不是保存一个排序的开放集,并一次访问一个结点。这涉及到HOT 队列方法。