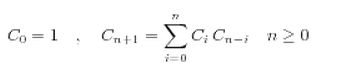作者:寒小阳 时间:2013年9月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/11596001。
声明:版权所有,转载请注明出处,谢谢。
0、前言
当年博主自己参加校招笔试面试时就遇到过几次catalan数相关的题目,今年又到了互联网招聘季,翻看下近期各大公司的笔试面试题,发现它依旧是很容易被考察的点。尴尬的是,博主自己觉得catalan数相关的题目不好归类到某种具体的数据结构或者算法里面(计算catalan数的那个小程序不算算法吧。。。),而是比较偏数学题。
不管怎么说,它是笔试面试中容易出现的东西,而有一部分同学可能不大熟悉。这里把catalan数的由来和笔试面试中涉及它的相关问题整理了一下,单独发一篇文吧,不熟悉的童鞋们看看,可能会有帮助。
一、catalan数由来和性质
1)由来
catalan数(卡塔兰数)取自组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
卡塔兰数的一般项公式为
令其为h(n)的话,满足
我们从中取出的Cn就叫做第n个Catalan数,前几个Catalan数是:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …咋看之下没什么特别的,但是Catalan数却是许多计数问题的最终形式。
2)性质
1、Catalan数的基本公式就是上面列出的式子,但是却有一些变形和具体的性质:
这是根据原来的式子推导出来的,大概过程是这样的:
2、有如下的递推式
3、有
4、
二、Catalan数的程序求解
//函数功能: 计算Catalan数列的第n项
//函数参数: 项数n
//返回值: 第n个Catalan数
long Catalan(int n)
{
if(n <= 1)
return 1;
long *h = new long[n+1]; //保存临时结果
h[0] = h[1] = 1; //h(0)和h(1)
for(int i = 2; i <= n; i++) //依次计算h(2),h(3)...h(n)
{
h[i] = 0;
for(int j = 0; j < i; j++) //根据递归式计算 h(i)= h(0)*h(i-1)+h(1)*h(i-2) + ... + h(i-1)h(0)
h[i] += (h[j] * h[i-1-j]);
}
long result = h[n]; //保存结果
delete [] h; //注意释放空间
return result;
}
三、Catalan数的应用场景和笔试面试中出现过的题目
1、括号匹配问题
n对括号相当于有2n个符号,n个左括号、n个右括号,可以设问题的解为f(2n)。第0个符号肯定为左括号,与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符,那么第0个字符与第2i个字符间包含奇数个字符,而奇数个字符是无法构成匹配的。
通过简单分析,f(2n)可以转化如下的递推式 f(2n) = f(0)f(2n-2) + f(2)f(2n - 4) + ... + f(2n - 4)f(2) + f(2n-2)f(0)。简单解释一下,f(0) * f(2n-2)表示第0个字符与第1个字符匹配,同时剩余字符分成两个部分,一部分为0个字符,另一部分为2n-2个字符,然后对这两部分求解。f(2)*f(2n-4)表示第0个字符与第3个字符匹配,同时剩余字符分成两个部分,一部分为2个字符,另一部分为2n-4个字符。依次类推。
假设f(0) = 1,计算一下开始几项,f(2) = 1, f(4) = 2, f(6) = 5。结合递归式,不难发现f(2n) 等于h(n)。
2、进栈出栈问题
这个与加括号的很相似,进栈操作相当于是左括号,而出栈操作相当于右括号。n个数的进栈次序和出栈次序构成了一个含2n个数字的序列。第0个数字肯定是进栈的数,这个数相应的出栈的数一定是第2i+1个数。因为如果是2i,那么中间包含了奇数个数,这奇数个肯定无法构成进栈出栈序列。
设问题的解为f(2n), 那么f(2n) = f(0)f(2n-2) + f(2)f(2n-4) + f(2n-2)f(0)。f(0) * f(2n-2)表示第0个数字进栈后立即出栈,此时这个数字的进栈与出栈间包含的数字个数为0,剩余为2n-2个数。f(2)f(2n-4)表示第0个数字进栈与出栈间包含了2个数字,相当于1 2 2 1,剩余为2n-4个数字。依次类推。
假设f(0) = 1,计算一下开始几项,f(2) = 1, f(4) = 2, f(6) = 5。结合递归式,不难发现f(2n) 等于h(n)。
3、二叉树的种类问题
可以这样考虑,根肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式,T(0, n-1),T(1, n-2),...T(n-1, 0),设T(i, j)表示根的左子树含i个结点,右子树含j个结点。
设问题的解为f(n),那么f(n) = f(0)f(n-1) + f(1)f(n-2) + .......+ f(n-2)f(1) + f(n-1)f(0)。假设f(0) = 1,那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式,不难发现f(n)等于h(n)。
4、网格路径问题
我们将一条水平边记为进栈,垂直边记为出栈,我们所要保证的就是前k步中水平边的个数不小于垂直边的个数,换句话说出栈的时候栈内一直有元素,所以从根本上说又回归到Catalan数了。
5、凸多边形分割问题
以凸多边形的一边为基,设这条边的2个顶点为A和B。从剩余顶点中选1个,可以将凸多边形分成三个部分,中间是一个三角形,左右两边分别是两个凸多边形,然后求解左右两个凸多边形。
设问题的解f(n),其中n表示顶点数,那么f(n) = f(2)f(n-1) + f(3)f(n-2) + ......f(n-2)f(3) + f(n-1)f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形,那么另外两个部分的顶点数分别为2和n-1。
设f(2) = 1,那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式,不难发现f(n) 等于h(n-2)。
6、集合划分问题
这里解释一下不交叉划分,我们对于集合{a,b}和{c,d},假设他们组成了两个区间[a,b]和[c,d],我们假设两个区间不重合,那么以下四种情况当做是不交叉的:a 对于集合{1,2,3...2n},将里面元素两两分为一子集,共n个,若任意两个子集都是不交叉的,那么我们称此时的这个划分为一个不交叉划分。此时不交叉的划分数就是我们的了,证明也很容易,我们将每个子集中较小的数用左括号代替,较大的用右括号代替,那么带入原来的1至2n的序列中就形成了合法括号问题,就是我们之前得到过的结论。例如我们的集合{1,2,3,4,5,6}的不交叉划分有五个:{{1,2},{3,4},{5,6}},{{1,2},{3,6},{4,5}},{{1,4},{2,3},{5,6}},{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。 7、阶梯切分问题 这个证明是怎么进行的呢?我们先绘制如下的一张图片,即n为5的时候的阶梯: 我们注意到每个切割出来的矩形都必需包括一块标示为的小正方形,那么我们此时枚举每个与#标示的两角作为矩形,剩下的两个小阶梯就是我们的两个更小的子问题了,于是我们的C5 = C0 * C4 + C1 * C3 + C2 * C2 + C1 * C3 + C0 * C4,注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。 8、乘积重组问题 我们这样考虑,首先通过括号化,将P分成两个部分,然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an),然后再对(a1)和(a2×a3.....×an)分别括号化;又如分成(a1×a2)×(a3.....×an),然后再对(a1×a2)和(a3.....×an)括号化。 设n个矩阵的括号化方案的种数为f(n),那么问题的解为 f(n) = f(1)f(n-1) + f(2)f(n-2) + f(3)f(n-3) + f(n-1)f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分,然后分别括号化。 计算开始几项,f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式,不难发现f(n)等于h(n-1)。 9、连线不想交问题 我们这样考虑,以其中一个点为基点,编号为0,然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数,否则,这两个编号间含有奇数个点,势必会有个点被孤立,即在一条线段的两侧分别有一个孤立点,从而导致两线段相交。设选中的基点为A,与它连接的点为B,那么A和B将所有点分成两个部分,一部分位于A、B的左边,另一部分位于A、B的右边。然后分别对这两部分求解即可。 设问题的解f(n),那么f(n) = f(0)f(n-2) + f(2)f(n-4) + f(4)f(n-6) + ......f(n-4)f(2) + f(n-2)f(0)。f(0)f(n-2)表示编号0的点与编号1的点相连,此时位于它们右边的点的个数为0,而位于它们左边的点为2n-2。依次类推。 f(0) = 1, f(2) = 1, f(4) = 2。结合递归式,不难发现f(2n) 等于h(n)。 10、高矮排队问题 先将2n个人从低到高排列,然后,用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有n个0,n个1的序列,就对应一种方案. 而010101...01对应着 第一排:1 3 5 ...2n-1 观察1的出现,我们考虑它能不能放在第二排,显然,在这个1之前出现的那些0和1对应的人 要么是在这个1左边,要么是在这个1前面。而即使前面0和1刚好配对,也一定要留出一个0在这个1前面,也就是要求之前的0的个数大于1的个数. 如果把0看成入栈操作,1看成出栈操作,就是说给定2n个元素,合法的入栈出栈序列有多少个。这就是catalan数,其通项是c(2n, n)/(n+1). 11、格子填数问题 这一题和上一题排队是一样的思路。 12、门票找钱问题 可以将持5元买票视为进栈,那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用三的分析直接得到结果,f(2n) 等于h(n)。 上面第12小题的一个延伸:n+m个人排队买票,并且满足n>= m,票价为5元,其中n个人各手持一张5元钞票,m个人各手持一张10元钞票,除此之外大家身上没有任何其他的钱币,并且初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。 这个题目是Catalan数的变形,不考虑人与人的差异,如果m=n的话那么就是我们初始的Catalan数问题,也就是将手持5元的人看成是入栈,手持10元的人看成是出栈,出栈序列的个数。 这个题目区别就在于n>m的情况,此时我们仍然可以用原先的证明方法考虑,假设我们要的情况数是D(n+m),无法让每个人都买到的情况数是U(n + m),那么就有D(n+m) + U(n +m) = C(m+n, n),此时我们求U(n + m),我们假设最早买不到票的人编号是k,他手持的是10元并且售票处没有钱,那么将前k个人的钱从5元变成10元,从10元变成5元,这时候就有n+1个人手持5元,m-1个手持10元的,所以就得到U(n + m) = C(n + m, n + 1),于是我们的结果就因此得到了,表达式是D(n + m) = C(n + m, n) - C(n + m, n + 1)。
比如00...011...1就对应着
第一排:1 2 3 ...n
第二排:n+1 n+2 n+3 ...2n
第二排:2 4 6 ...2n
在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数
四、Catalan数的一个变形应用