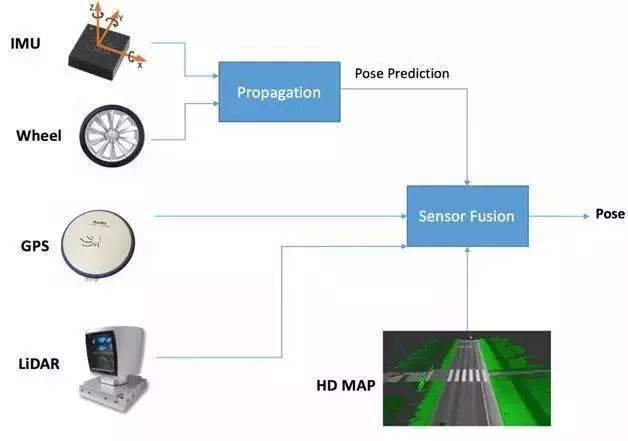
最小二乘法(Least Squares Method)可以在存在测量噪声的情况下,可以最大限度的剥离噪声的影响,求得最优解。
自动驾驶车辆配备了许多的不同的传感器,它们的测量精度各不相同,有的精度高,有的精度低,而高精度设备的测量结果更加值得信任,如何达到这种效果呢。一个直觉的做法,就是赋予高精度的测量更大的权重,同时降低低质量的测量结果的贡献。Weighted Least Square Method可以帮助达到这一目的。
1. Weighted Least Square Method
1.1 线性回归的一般形式:
$$ \begin{aligned} h_{\theta}(x) =& \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n \\ =& \theta^T x \end{aligned} $$
其中:
$$ x^{(i)} = \left[ \begin{matrix} x_1^{(i)} \\ x_2^{(i)} \\ \vdots \\ x_n^{(i)} \end{matrix} \right] X=\left[ \begin{matrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \vdots \\ (x^{(m)})^T \end{matrix} \right] Y = \left[ \begin{matrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{matrix} \right] $$
是观测测量值,m是观测测量值的数目。
$$ \theta=\left[ \begin{matrix} \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{matrix} \right] $$
是待估计参数, n是未知参数的个数。一般情况下m>n。
1.2 Weighted Least Square的目标函数
我们假设目标变量$y$和输入变量$x$存在如下关系:
$$ y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)} $$
$\epsilon^{(i)}$是测量误差项,它们独立同分布,并且服从标准正态分布$\epsilon^{(i)} \sim N(0,\sigma^2)$。
即:
$$ R=E(\epsilon_i \epsilon_i^T) =\left[ \begin{matrix} \sigma^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma^2 \end{matrix} \right] $$
如果假设$\epsilon^{(i)}$独立,但是有不同的方差(variance)。
$$ R=E(\epsilon_i \epsilon_i^T) =\left[ \begin{matrix} \sigma_1^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_m^2 \end{matrix} \right] $$
则Weighted Least Squares Method的目标函数可以定义如下:
$$ \begin{aligned} WLS\_J(\theta_1, \theta_2, ..., \theta_n) =& \frac{1}{2} \sum_{i=1}^{n}{w_i}(\theta^Tx^{(i)} - y^{(i)})^2 \\ =& \frac{1}{2} \sum_{i=1}^{n}\frac{(\theta^Tx^{(i)} - y^{(i)})^2}{\sigma_i^2} \\ =& \frac{1}{2} (X\theta - Y)^TR^{-1}(X\theta - Y) \\ \end{aligned} $$
1.3 Weighted Least Square的矩阵解
令导数为0,求解极值点:
$$ \begin{aligned} \frac{\partial WLS\_J(\theta_1, \theta_2, ..., \theta_n)}{\partial \theta} =& X^TR^{-1}X\theta - X^TR^{-1}Y \\ =& 0 \end{aligned} $$
可得到:
$$ \theta = (X^TR^{-1}X)^{-1} X^TR^{-1}Y $$
2. Weighted Least Squares的应用举例
仍以前一篇文章提到的测量车辆位置为例,展示Weighted Least Squares的用法。
假设存在m个测量值和n个未知参数:
$$ \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_m \\ \end{matrix} \right] =H \left[ \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{matrix} \right] + \left[ \begin{matrix} e_1 \\ e_2 \\ \vdots \\ e_m \\ \end{matrix} \right] $$
Weighted Least Squares的目标函数如下:
$$ WLS\_J=e^T R^{-1} e $$
其中:
$$ \left[ \begin{matrix} e_1 \\ e_2 \\ \vdots \\ e_m \\ \end{matrix} \right]=e= \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_m \\ \end{matrix} \right] - H \left[ \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{matrix} \right] $$
$$ H=\left[ \begin{matrix} 1 \\ 1 \\ \vdots \\ 1 \\ \end{matrix} \right] $$
令:
$$ \frac{\partial (WLS\_J)}{\partial X} = 0 = -Y^TR^{-1}H+X^TH^TR^{-1}H $$
得到:
$$ X = (H^TR^{-1}H)^{-1} H^TR^{-1}Y $$
假设有激光雷达和卫星同时对自动驾驶车辆进行位置测量,测量结果如下:
| 测量设备 | 车辆位置 | 方差 |
|---|---|---|
| 卫星1 | 1.80 | 400 |
| 卫星2 | 1.78 | 400 |
| 卫星3 | 1.82 | 400 |
| 激光雷达1 | 1.89 | 4 |
| 激光雷达2 | 1.90 | 4 |
代入上式:
$$ X=\Bigg( \left[ 1, 1, 1,1,1 \right] \left[ \begin{matrix} 400 & & & & \\ & 400 & & & \\ & & 400 & &\\ & & & 4 & \\ & & & & 4 \\ \end{matrix} \right]^{-1} \left[ \begin{matrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{matrix} \right] \Bigg)^{-1} \left[ 1, 1, 1,1,1 \right] \left[ \begin{matrix} 400 & & & & \\ & 400 & & & \\ & & 400 & &\\ & & & 4 & \\ & & & & 4 \\ \end{matrix} \right]^{-1} \left[ \begin{matrix} 1.80 \\ 1.78 \\ 1.82 \\ 1.89 \\ 1.90 \\ \end{matrix} \right] = 1.89 $$
可以看到,Weighted Least Square的计算结果更接近于方差较小的激光雷达测量结果。
相关文章
自动驾驶定位系统-State Estimation & Localization
个人网站地址: http://www.banbeichadexiaojiu...