一:概述
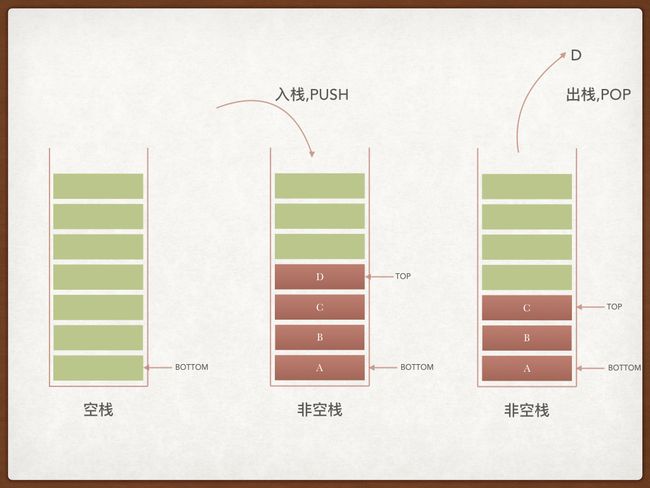
由图我们可看成栈只能从栈顶存取元素,同时先进入的元素反而是后出,而栈顶永远指向栈内最顶部的元素。到此可以给出栈的正式定义:栈(Stack)是一种有序特殊的线性表,只能在表的一端(称为栈顶,top,总是指向栈顶元素)执行插入和删除操作,最后插入的元素将第一个被删除,因此栈也称为后进先出(Last In First Out,LIFO)或先进后出(First In Last Out FILO)的线性表。栈的基本操作创建栈,判空,入栈,出栈,获取栈顶元素等,注意栈不支持对指定位置进行删除,插入,其接口Stack声明如下:
public interface Stack {
// 栈是否为空
boolean isEmpty();
// 入栈
void push(T data);
// 取出栈顶元素,不出栈
T peek();
// 出栈
T pop();
}
二:顺序栈的设计与实现
顺序栈,顾名思义就是采用顺序表实现的的栈,顺序栈的内部以顺序表为基础,实现对元素的存取操作,当然我们还可以采用内部数组实现顺序栈,在这里我们使用内部数据组来实现栈:
public class SeqStack implements Stack{
//栈顶索引,-1代表空栈
private int top = -1;
//默认容量大小
private int capacity = 10;
//存放数据的数组
private T[] arr;
//栈的实际使用量
private int size;
public SeqStack() {
arr = (T[]) new Object[capacity];
}
//是否是空栈的判断依据是top是否为-1;如果大于等于0,说明栈中有元素
@Override
public boolean isEmpty() {
return top == -1;
}
//获取栈顶元素,本例基于数组来实现栈,所以栈顶元素,就是数组的最后一个元素
@Override
public T peek() {
//如果是空栈就抛出异常
if(isEmpty()) {
new EmptyStackException();
}
//返回数组的最后一个元素
return arr[top];
}
//获取栈顶元素并出栈
@Override
public T pop() {
//国际惯例,空栈抛出异常
if(isEmpty()) {
new EmptyStackException();
}
size --;
//需要注意的是,这里不会将数组的最后一个元素置空,因为top的值已经修改
//下次再push的时候只是把原来的数组元素的值进行了修改,因为一旦pop后,
//top的值减小了,原来的数组的元素永远访问不到,完全没有必要置空.
return arr[top--];
}
//入栈
@Override
public void push(T data) {
//如果栈已满,那么扩容
if(size == arr.length) {
ensureCapacity(size*2+1);
}
//先将栈顶指针+1,然后将元素放入top + 1那个位置
arr[++top] = data;
size++;
}
//扩容的思路很简单,创建一个新的数组,然后将原来数组的数据复制到新数组
private void ensureCapacity(int capacity) {
//以防万一
if(capacity > size) {
return;
}
T[] old = arr;
arr = (T[]) new Object[capacity];
for(int i = 0 ; i < old.length ; i++) {
arr[i] = old[i];
}
}
}
测试代码:
public static void main(String[] args) {
SeqStack stack = new SeqStack<>();
stack.push("A");
stack.push("B");
stack.push("C");
stack.push("D");
int l = stack.size;
System.out.println("size : " + l + " , top index : " + stack.top +
" , top : " + stack.peek());
for(int i = 0 ; i < l; i ++) {
stack.pop();
}
//此处抛出异常
System.out.println("size : " + l + " , top : " + stack.peek());
}
测试结果:
push A , size : 1
push B , size : 2
push C , size : 3
push D , size : 4
size : 4 , top index : 3 , top : D
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: -1
at teststack.SeqStack.peek(SeqStack.java:58)
at teststack.SeqStack.main(SeqStack.java:42)
从上面可以看出,顺序栈的逻辑很简单,就是操作底层的数组而已,所有的入栈和出栈操作,都是往数组添加和删除元素,然后改变top指针的位置。
以上就是顺序栈的实现,简单。
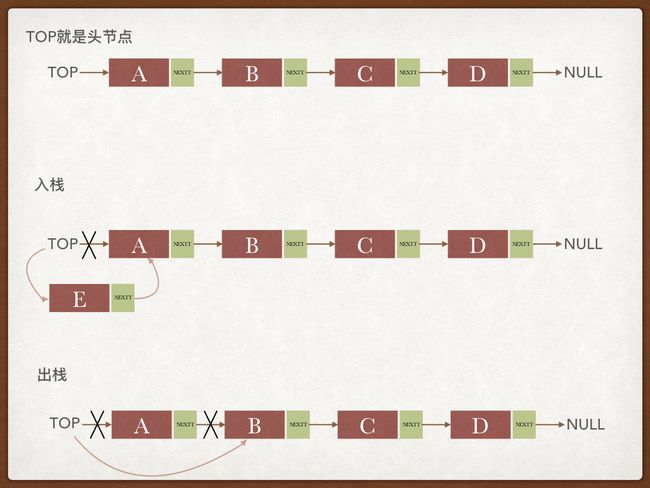
三:链式栈的设计与实现
public class LinkStack implements Stack{
//栈顶元素
private Node top;
private int size;
public LinkStack() {
top = new Node();
}
//如果栈顶元素为空,或者栈顶元素的数据为空,一律视为空栈
@Override
public boolean isEmpty() {
return top == null || top.data == null;
}
@Override
public void push(T data) {
if (data == null) {
try {
throw new Exception("data can\'t be null");
} catch (Exception e) {
e.printStackTrace();
}
}
//如果栈顶节点是空的话,那么创建一个新的节点当做栈顶节点
if (top == null) {
top = new Node<>(data);
//如果栈顶节点的数据为空的话,那么将数据赋值给该节点
} else if (top.data == null) {
top.data = data;
//如果栈顶节点和数据都不为空,说明不是空栈,这时候需要创建一个
//新的节点,将它赋值给栈顶节点,同时将它的next指向当前的栈顶节点
} else {
Node p = new Node(data, this.top);
top = p;
}
size++;
}
// 获取栈顶元素,我们一直持有栈顶节点的引用,直接返回好了
@Override
public T peek() {
if (isEmpty()) {
new EmptyStackException();
}
return top.data;
}
//出栈,就是将栈顶节点的下一个节点当做新的栈顶节点,
//实质上就是移除链表中的头结点,很简单
@Override
public T pop() {
if (isEmpty()) {
new EmptyStackException();
}
T data = top.data;
top = top.next;
size--;
return data;
}
//节点
class Node {
public T data;
public Node next;
public Node() {
}
public Node(T data) {
this.data = data;
}
public Node(T data, Node next) {
this.data = data;
this.next = next;
}
}
测试代码:
public static void main(String[] args) {
LinkStack sl = new LinkStack<>();
sl.push("A");
sl.push("B");
sl.push("C");
int length = sl.size;
for (int i = 0; i < length; i++) {
System.out.println("sl.pop->" + sl.pop() + " , size : " + sl.size);
}
sl.push("T");
System.out.println("sl.pop->" + sl.peek() + " , size : " + sl.size);
}
测试结果:
sl.pop->C , size : 2
sl.pop->B , size : 1
sl.pop->A , size : 0
sl.pop->T , size : 1
综上可知,栈的实现还是很简单的,下面讲下栈的应用场景。
四:栈的应用
栈是一种很重要的数据结构,在计算机中有着很广泛的应用,如下一些操作都应用到了栈:
符号匹配
中缀表达式转换为后缀表达式
计算后缀表达式
实现函数的嵌套调用
HTML和XML文件中的标签匹配
网页浏览器中已访问页面的历史记录
符号匹配:
在编写程序的过程中,我们经常会遇到诸如圆括号“()”与花括号“{}”,这些符号都必须是左右匹配的,这就是我们所说的符合匹配类型,当然符合不仅需要个数相等,而且需要先左后右的依次出现,否则就不符合匹配规则,如“)(”,明显是错误的匹配,而“()”才是正确的匹配。有时候符合如括号还会嵌套出现,如“9-(5+(5+1))”,而嵌套的匹配原则是一个右括号与其前面最近的一个括号匹配,事实上编译器帮我检查语法错误是也是执行一样的匹配原理,而这一系列操作都需要借助栈来完成,接下来我们使用栈来实现括号”()”是否匹配的检测。
判断原则如下(str=”((5-3)*8-2)”):
a.设置str是一个表达式字符串,从左到右依次对字符串str中的每个字符char进行语法检测,如果char是,左括号则入栈,如果char是右括号则出栈(有一对匹配就可以去匹配一个左括号,因此可以出栈),若此时出栈的字符char为左括号,则说明这一对括号匹配正常,如果此时栈为空或者出栈字符不为左括号,则表示缺少与char匹配的左括号,即目前不完整。
b.重复执行a操作,直到str检测结束,如果此时栈为空,则全部括号匹配,如果栈中还有左括号,是说明缺少右括号。
接着我们用栈作为存储容器通过代码来实现这个过程
public class CheckExpression {
public static String isValid(String expstr){
//创建栈
LinkedStack stack = new LinkedStack<>();
int i = 0 ;
//遍历字符串,挨个取出每个字符
while(i < expstr.lenght()){
char c = expstr.charAt(i);
i++;
switch (ch){
//如果该字符是左括号,那么放入栈中
case '(' :
stack.push(ch + "");
break;
//如果是右括号,那么将左括号出栈
case ")" :
if(stack.isEmpty() || !stack.pop().equals("(")) {
return "FAILURE";
}
}
}
//经过这么一轮循环,如果栈为空,说明每个左括号都有
//右括号和他匹配,这时候校验通过,否则不通过
if(stack.isEmpty()) {
return "PASS";
}else {
return "FAILURE";
}
}
}
测试代码:
String expstr="((5-3)*8-2)";
System.out.println(expstr + " check " + check(expstr));
String expstr1="((5-3)*8-2";
System.out.println(expstr1 + " check " + check(expstr1));
测试结果:
((5-3)*8-2) check PASS
((5-3)*8-2 check FAILURE
摘自:https://blog.csdn.net/javazejian/article/details/53362993