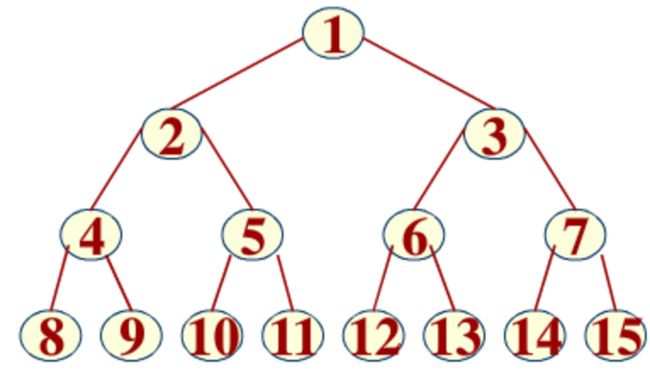
完全二叉树的基本概念
可能你会疑问,为什么我们明明讲的是堆排序,怎么又扯上了二叉树的概念了,答案就是,我们这里的堆就是基于完全二叉树来的,我们称之为最大堆,所谓的完全二叉树其实是相对于满二叉树而言的,这里我们不去深究二叉树之类的这些概念,因为我们主要是讨论堆排序,下面我上两张图你就能明白满二叉树是什么,完全二叉树是什么了:
满二叉树的所有分支结点都既有左子树又有右子树,并且所有叶子都在同一层。满二叉树就是感觉是满的没有残缺。
而完全二叉树不一定是满的,但它自上而下,自左而右来看的话,是连续没有缺失的。
完全二叉树的特性
上面已经介绍了完全二叉树的概念,这里我还需要总结一下完全二叉树的特性,因为我们后面需要用到这些特性来撸代码:
这里我们假如使用数组来实现这个最大堆,数据从 1 的位置开始存储,第0的索引我们不存放东西,那么就有如下性质:
1.父亲节点的索引parent = i /2 向下取整例如 这里2是4和5的父亲节点,那么2 = 5/2,向下取整等于2;
2.第一个无叶子的节点的索引等于整个堆的元素个数除以2 ,k = count / 2;
3.左孩子的索引等于父节点的索引除以2, k = 2 * i,而右孩子就等于2 * i + 1
最大堆的实现/优先队列的概念
这里我还是想简单介绍一个场景,这样大家理解起来会比较容易,假如我们是一个游戏玩家--例如王者荣耀的玩家,那么每一个英雄都有一个攻击的范围,假如这个范围内出现了多个敌方英雄或者小兵,那么你可以攻击他们任意一个,但是他会有一个优先级,你可以攻击英雄 也可以攻击小兵,假如你得需求是每次你都优先攻击英雄,那么让你来实现这个需求,你会怎么做呢?这就是我们的优先队列或者说最大堆;
最大堆/优先队列的实现
下面就是我们最大堆或者说优先队列的实现了,假如我们使用一个类来实现这个最大堆,我们先思考一下我们需要哪些方法?
首先我觉得有最重要的几个方法,实例化方法、入队和出队
/**
实例化最大堆
@param capacity 堆中的最大容量
@return 最大堆实例
*/
+ (instancetype)maxHeapWithCapacity:(NSInteger)capacity;
/**
插入值到最大堆中(入队)
@param item 元素
*/
- (void)insertItem:(id)item;
/**
从堆中取值(出队)
@return 优先的元素
*/
- (id)extractMax;
接下来我们可能还需给外界提供一个获取当前堆中容量和是否是一个空堆的方法
/**
最大堆中的大小
@return 堆容量
*/
- (NSInteger)size;
/**
判断是否为空堆
@return 是否空堆
*/
- (BOOL)isEmpty;
好了,我们就根据我们提出的这几个方法来依次实现以下:
1.实例化方法 (MaxHeap类的实例化)
再讲实例化方法之前,我们先把存放元素的数组和一些其它需要用到的属性声明好,当然这些都是不提供给外界的,所以我们都放在.m中
/** 堆容量 */
@property(nonatomic,assign) NSInteger capacity;
/** 数据个数*/
@property(nonatomic,assign) int count;
/** 容器 */
@property(nonatomic,strong) NSMutableArray *itemsArray;
- (NSMutableArray *)itemsArray {
if (!_itemsArray) {
_itemsArray = [NSMutableArray arrayWithCapacity:self.capacity + 1];
//默认先加入一个元素 也就是第0个元素
[_itemsArray addObject:@(0)];
}
return _itemsArray;
}
有了上面这些,我们的实例化方法就出来了:
+ (instancetype)maxHeapWithCapacity:(NSInteger)capacity {
MaxHeap *maxHeap = [[MaxHeap alloc]init];
maxHeap.capacity = capacity;
maxHeap.count = 0;
return maxHeap;
}
上面的代码我就不用解释了吧,capacity是数组最大容量,而count是我们的元素真实的个数,当然我们在懒加载中可能你注意到了一个地方,那就是我在初始化itemArray的时候默认是添加了一个元素的,原因是我们的最大堆是从第一个元素开始的,而第一个元素我们不需要用到,所以这里默认第一个元素就直接用0来代替
2.入队操作的实现
- (void)insertItem:(id)item {
if (self.count >= self.capacity) {
//这里也可以用断言
NSLog(@"容量已满");
return;
}
//添加元素
[self.itemsArray addObject:item];
//元素个数++
self.count++;
//执行shiftUp操作
[self shiftUp:_count];
}
/**
不断与父亲节点比较往上升的过程
@param k 比较的索引
*/
- (void)shiftUp:(int)k {
//当k == 1的时候只有一个元素就可以不用比较了 self.itemsArray[k/2]是父亲节点的值
while (k > 1 && self.itemsArray[k] > self.itemsArray[k/2]) {
//交换位置
[self.itemsArray exchangeObjectAtIndex:k/2 withObjectAtIndex:k];
//更新索引为父节点的索引
k /= 2;
}
}
3.出队列操作的实现
- (id)extractMax {
if (self.count <= 0) {
NSLog(@"无法取出元素---堆中元素已全部取出");
return nil;
}
//将当前最大的数也就是第一个元素取出来
id item = self.itemsArray[1];
//将最后一个元素放到第一位
[self.itemsArray exchangeObjectAtIndex:1 withObjectAtIndex:self.count];
self.count--;
//执行shiftDown操作
[self shiftDown:1];
return item;
}
- (void)shiftDown:(int)k {
while (2*k <= _count) {//判断是否有孩子 只要判断的有左孩子就行了
//声明一个变量初始化为做左孩子的索引
int j = 2 *k;
//判断是否右孩子防止越界且比较左孩子和右孩子的值
if (j + 1 <= _count && _itemsArray[j] < _itemsArray[j + 1]) {
j += 1;
}
//此时itemsArray[j]中存放的就是两个孩子中间最大的元素
//比较父节点与孩子中最大的值
if (_itemsArray[j] <= _itemsArray[k]) {
break;
}
//走到这里说明父节点比子节点的值要小 交换位置 更新索引
[_itemsArray exchangeObjectAtIndex:j withObjectAtIndex:k];
k = j;
}
}
4.元素个数以及判空实现
- (NSInteger)size {
return self.count;
}
- (BOOL)isEmpty {
return self.count == 0;
}
第一个版本的堆排序
到这里,我们已经基本实现了一个优先队列或者说最大堆了,此外我们的第一个版本的堆排序也已经完成了,可能你就会纳闷了,你写了这么多好像也没看到排序啊,我到底外界怎么使用呢?别急,下面就告诉你怎么用:
/**
第一个版本的堆排序
@param originalArray 待排序数组
*/
- (void)heapSort1:(NSMutableArray *)originalArray {
//1.实例化最大堆
MaxHeap *maxHeap = [MaxHeap maxHeapWithCapacity:originalArray.count];
//2.将所有数组中的元素入队
[originalArray enumerateObjectsUsingBlock:^(id _Nonnull obj, NSUInteger idx, BOOL * _Nonnull stop) {
[maxHeap insertItem:obj];
}];
//3.从堆中依次取出元素赋值给array(出队)
for (int i = (int)originalArray.count - 1; i >= 0; i--) {
originalArray[i] = maxHeap.extractMax;
}
}
好了,就这么简单,运行然后打印一下要排序的数组,是不是觉得很神奇?原来排序还可以这样实现,第一次看到堆排序的时候我也觉得超神奇,所以说还是应该要多学习,你会收获到很多你意想不到的东西。
第二个版本的堆排序(heapify)
可能你会纳闷了,不是已经都实现完了吗?怎么还有第二个版本,呵呵,我只能说:“骚年,你还太年轻,除了第二个版本,还有第三个”。别急,看完上一个版本的堆排序,可能你会问,第二个版本的堆排序是为了解决什么?答案是减少时间复杂度呀。废话不多少,下面还是先把图上了:
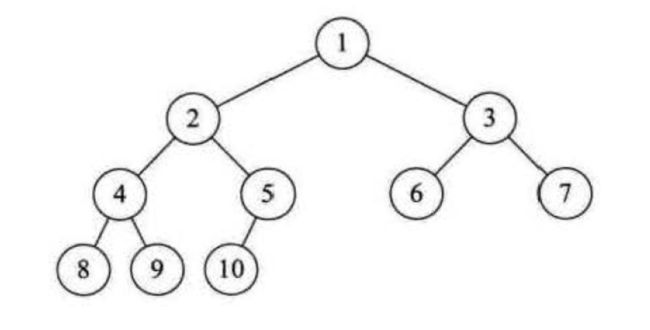
前面我们提到了完全二叉树的特性2:
第一个无叶子的节点的索引等于整个堆的元素个数除以2 ,k = count / 2;
从图中我们可以看到第一个无叶子节点的索引多少呢?
答案是 5,也就是 10 / 2 = 5,那我们拿到这个有什么用呢?大家注意看,如果我们从5号索引开始依次递减执行我们在上面实现的shiftDown方法会怎样呢?,看出什么了吗,你会发现是不是执行完之后,这个数组内的元素已经是一个最大堆了呢?没错就是这么简单,下面是代码实现:
.h中
/**
实例化最大堆
@param orginalArray 待排序数组
@return 最大堆
*/
+ (instancetype)maxHeapWithOriginalArray:(NSMutableArray *)orginalArray;
.m中
+ (instancetype)maxHeapWithOriginalArray:(NSMutableArray *)orginalArray {
MaxHeap *maxHeap = [[MaxHeap alloc]init];
//因为索引是从1开始添加数据 所以这里要加1
maxHeap.capacity = (int)orginalArray.count + 1;
maxHeap.count = (int)orginalArray.count;
//依次将数组中的元素添加到itemArray中
[orginalArray enumerateObjectsUsingBlock:^(id _Nonnull obj, NSUInteger idx, BOOL * _Nonnull stop) {
[maxHeap.itemsArray addObject:obj];
}];
//从第一个无叶子节点开始依次执行shiftDown操作
for (int i = maxHeap.count/2; i >= 1; i--) {
[maxHeap shiftDown:i];
}
return maxHeap;
}
那么怎么使用呢?
/**
堆排序第二个版本
@param originalArray 待排序数组
*/
- (void)heapSort2:(NSMutableArray *)originalArray {
//实例化优先队列
MaxHeap *maxHeap = [MaxHeap maxHeapWithOriginalArray:originalArray];
for (int i = (int)originalArray.count - 1; i >= 0; i--) {
//依次出队列就可以了
originalArray[i] = maxHeap.extractMax;
}
}
看到这里,赶紧去试一下效果吧,你是不是也会惊叹:"还有这操作",这里可能很多人会说,既然你是为了优化时间复杂度而来的第二个版本,那么你用代码来测试一下啊,其实我也想在这里就直接来个测试截图,这样这篇文章就结束了,当然这是我不愿意看到的,因为如果这样就结束了,那我第三个版本的堆排序该怎么进行呢?so,别着急,等我第三个版本的堆排序讲完了,给大家看最后的测试代码和结果。
第三个版本的堆排序(原地堆)
我们前面的两个版本排序都是属于先通过实现一个最大堆也就是新开辟了空间的基础上来实现的,那么有没有什么方式可以直接在原数组上面就实现呢?答案肯定是有的,有了第二个版本的的基础,其实我们也称第二个版本叫做heapify的过程,我们就可以直接在原数组上将数组heapify,再通过一定的交换操作来完成原地堆的排序:
第一步:将数组heapify
//1.先将数组heapify(形成最大堆)
for (int i = (int)(originalArray.count - 1)/2; i >= 0; i--) {
//依次执行shiftDown操作来实现最大堆
[self shiftDown:originalArray count:(int)originalArray.count index:i];
}
这里我就不再解释了,如果没有看懂怎么将数组heapify,那就往前再回顾一下,这里的shiftDown方法和原来第二个版本的shiftDown方法基本一样,但是由于我们是直接在原数组的基础上进行,索引是从0开始的,所以这里就会有一些差异,这些差异我在实现的代码里都标记了注释,所以这里我就先不讲,下面会给出shiftDown的代码,看到这里,数组已经是一个优先队列了,那么我们要排序,假如要将从小到大的排列,我们可以这样做:
1.将第0个位置的元素和最后一个位置的元素交换位置,此时最后一个元素就是最大的元素了
2.执行完上面的操作之后,你会发现除了最后一个元素之外也就是n - 1这些个元素现在已经不能满足最大堆的性质了,那么我们可以想办法让它继续满足最大堆的性质,具体怎么做呢?其实很简单,我们对数组n - 1个元素中的第0个位置的元素执行shiftDown操作就可以了
下面来看代码:
/**
原地堆排序--堆排序第三个版本
@param originalArray 待排序数组
*/
- (void)heapSort3:(NSMutableArray *)originalArray {
//1.先将数组heapify(形成最大堆)
for (int i = (int)(originalArray.count - 1)/2; i >= 0; i--) {
[self shiftDown:originalArray count:(int)originalArray.count index:i];
}
//2.将最大堆中的第一个元素也就是最大的元素 放到数组最后
for (int j = (int)originalArray.count - 1; j >=0 ; --j) {
[originalArray exchangeObjectAtIndex:0 withObjectAtIndex:j];
//交换完位置后再执行shiftDown操作让数组前半部分保持最大堆的性质
[self shiftDown:originalArray count:j index:0];
}
}
/**
shiftDown操作
@param array 待排序数组
@param count shifDown操作界限
@param index shiftDown的位置
*/
- (void)shiftDown:(NSMutableArray *)array count:(int)count index:(int)index{
//因为是从0开始 所以左孩子就应该要偏移1个位置
while (2*index + 1 < count) {//判断只要有孩子(有左孩子就表示有孩子)
int j = 2*index + 1;//初始化j为左孩子索引
if (j + 1 < count && array[j] < array[j+1]) {//第一个判断条件为右孩子是否越界,判断左孩子是否比右孩子的值大
j += 1;//j+1 索引变为右孩子的索引
}
if (array[index] >= array[j]) {//判断父亲节点的值和子孩子的值进行比较
break;
}
//当父亲节点的值比孩子节点的值要大舅应该交换位置
[array exchangeObjectAtIndex:index withObjectAtIndex:j];
//更新索引
index = j;
}
}
可能会有很多人对下面这一部分代码不理解:
//2.将最大堆中的第一个元素也就是最大的元素 放到数组最后
for (int j = (int)originalArray.count - 1; j >=0 ; --j) {
[originalArray exchangeObjectAtIndex:0 withObjectAtIndex:j];
//交换完位置后再执行shiftDown操作让数组前半部分保持最大堆的性质
[self shiftDown:originalArray count:j index:0];
}
我这里简单的解释一下,我们这里的j就是从count - 1开始,这是因为我们交换完成之后让前半部分没有交换的元素依然保持最大堆的性质,如果从0开始则没法控制这个j的索引,而下面的shiftDown操作中count传入的恰好是j,也就是要维持最大堆性质的个数,当然这里的index是要执行shiftDown操作的索引,这里很简单就是第一个元素啦,因为交换位置后,最大的元素被移动到最后去啦,说到这里,今天要讨论的问题就结束了,但是我前面还说了要给大家提供三个版本堆排序的测试代码和结果的,所以还不能结束(哈哈_别哭)
测试代码 & 测试结果
- (void)testSortWithExcuteBlock:(void(^)())excuteBlock{
CFAbsoluteTime startTime =CFAbsoluteTimeGetCurrent();
if (excuteBlock) {
excuteBlock();
}
CFAbsoluteTime linkTime = (CFAbsoluteTimeGetCurrent() - startTime);
NSLog(@"Linked in %f ms", linkTime *1000.0);
}
上面是我在测试排序工具类中的方法,这里抽出来单独说一下,传入一个block,在外界调用后就可以拿到测试结果,下面开始测试:
NSMutableArray *array1 = [self.testHelper generateRandomArray:100000 rangeLeft:1 rangeRight:1000];
NSMutableArray * heapSort1 = array1.mutableCopy;
NSMutableArray * heapSort2 = array1.mutableCopy;
NSMutableArray * heapSort3 = array1.mutableCopy;
NSLog(@"============第一个版本堆排序==============");
[self.testHelper testSortWithExcuteBlock:^{
[self heapSort1:insertionSort1];
}];
NSLog(@"============第二个版本堆耗时==============");
[self.testHelper testSortWithExcuteBlock:^{
[self heapSort2:heapSort2];
}];
NSLog(@"============第三个版本堆耗时==============");
[self.testHelper testSortWithExcuteBlock:^{
[self heapSort3:heapSort3];
}];
这里把生成代码的测试数组的方法贴出来,不然我怕有些朋友又要问这个怎么来的了:
#pragma mark - 随机获取一个数组
#pragma mark -
- (NSMutableArray *)generateRandomArray:(int)count rangeLeft:(int)left rangeRight:(int)right{
NSMutableArray * tempArray = [NSMutableArray arrayWithCapacity:count];
for (int i = 0; i < count; i ++) {
int randomNum = arc4random()%(right - left + 1) + left;
[tempArray addObject:@(randomNum)];
}
return tempArray;
}
这里的testHelper就是我的测试工具类,这里你可以忽略,反正就是用来帮助测试代码执行时长的,这里我也把随机生成一个数组的方法提供了,这里我用的数据是10万个数据进行排序,,下面是测试结果:
我们可以明显的看到三个版本的堆排序时间是依次递减的,也就是说我们的优化还是挺有成效是不是(哈哈)
好吧,如果你认真的再看这篇文章的话,可能看到这里你也很累了,说实话,我更累啊 ,码字、截图、测试好累好累,希望可以帮到大家,有什么不懂得依旧留言或者私信哦。