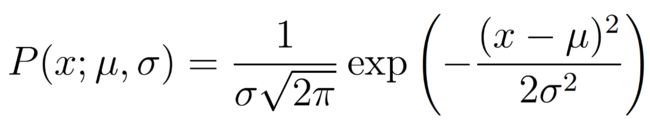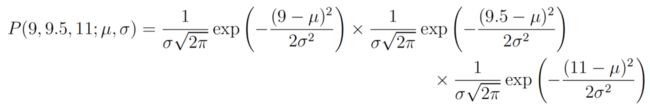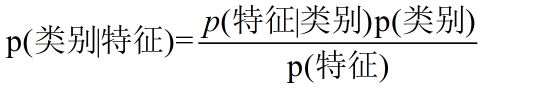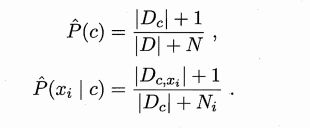参数估计是机器学习里面的一个重要主题，而极大似然估计是最传统、使用最广泛的估计方法之一。
在讲最大似然估计和贝叶斯估计之前，先来谈谈概率和统计的区别吧。
概率和统计是一个东西吗？
概率（probabilty）和统计（statistics）看似两个相近的概念，其实研究的问题刚好相反。
概率研究的问题是，已知一个模型和参数（例如均值，方差，协方差等等），怎么去预测这个模型产生的结果的特性。 举个例子，我想研究怎么养猪（模型是猪），我选好了想养的品种、喂养方式、猪棚的设计等等（选择参数），我想知道我养出来的猪大概能有多肥，肉质怎么样（预测结果的概率）。
统计研究的问题则相反。统计是，有一堆数据，要利用这堆数据去预测模型和参数。仍以猪为例。现在我买到了一堆肉，通过观察和判断，我确定这是猪肉（这就确定了模型。在实际研究中，也是通过观察数据推测模型是／像高斯分布的、指数分布的、拉普拉斯分布的等等），然后，可以进一步研究，判定这猪的品种、这是圈养猪还是跑山猪还是网易猪，等等（推测模型参数）。
一句话总结：概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。
最大似然估计（maximum likelihood estimation）
最大似然估计是用来估计一个概率模型的参数的一种方法。确定参数值的过程，是找到能最大化模型产生真实观察数据可能性的那一组参数。
一个小栗子
现在有3个独立同分布的数字9, 9.5, 11（假设该分布为高斯分布），现在要估计此正态分布的参数值μ 和 σ ，利用最大似然估计该怎么求呢？
我们要计算的是同时观察到所有这些数据的概率，也就是所有观测数据点的联合概率分布。因此，我们需要计算一些可能很难算出来的条件概率。我们将在这里做出第一个假设，假设每个数据点都是独立于其他数据点生成的。这个假设能让计算更容易些。
如果事件（即生成数据的过程）是独立的，那么观察所有数据的总概率就是单独观察到每个数据点的概率的乘积（即边缘概率的乘积）。
很明显我们例子中的五个数字是符合上述条件的。因此，从高斯分布中生成的单个数据点 x 的（边缘）概率是：
我们只要找出能够让上述表达式最大化的μ、σ值就可以了。具体的求解过程包括取对数，求偏导为0时候的值便是我们要求的值了，这里就不进行求导了。
为什么叫「最大似然（最大可能性）」，而不是「最大概率」呢？
虽然大多数人倾向于混用「概率」和「似然度」这两个名词，但统计学家和概率理论家都会区分这两个概念，这是否只是这些学者在卖弄学识呢？当然不是，通过观察下面这个等式，我们可以更好地明确这种混淆的原因。这两个表达式是相等的！所以这是什么意思？我们先来定义 P(data; μ, σ) 它的意思是「在模型参数μ、σ条件下，观察到数据 data 的概率」。值得注意的是，我们可以将其推广到任意数量的参数和任何分布。
另一方面，L(μ, σ; data) 的意思是「我们在观察到一组数据 data 之后，参数μ、σ取特定的值的似然度。」
因此，结合文章开头部分对于概率和统计的讨论，我们有理由说似然度是站在统计的角度上来说的，即已知数据推导模型和参数。
贝叶斯估计
在开始介绍贝叶斯估计之前，让我们先来看看贝叶斯定理吧。
贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
在贝叶斯定理中，每个名词都有约定俗成的名称：
- P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
- P(A)是A的先验概率（或边缘概率）。之所以称为"先验"是因为它不考虑任何B方面的因素。
- P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率。
按这些术语，贝叶斯定理可表述为：
后验概率 = (似然性*先验概率)/标准化常量
也就是说，后验概率与先验概率和相似度的乘积成正比。
另外，比例P(B|A)/P(B)也有时被称作标准似然度（standardised likelihood），贝叶斯定理可表述为：
后验概率 = 标准似然度*先验概率
从条件概率和联合概率推导贝叶斯定理。事件A,B同时发生的概率（也即联合概率）为：
P(A,B)=P(A∩B)=P(A|B)P(B)
P(B,A)=P(B∩A)=P(B|A)P(A)
由于P(A,B)=P(B,A), 所以：
P(A|B)P(B)=P(B|A)P(A) =>
从全概率角度来试着解释下上式分母也即B事件边缘概率的意思：
P(B)=∑ iP(B|A i)*P(A i)
这个式子表示所有事件A i条件下观察到的B情况。因此，贝叶斯公式的一种变形为：
贝叶斯估计与贝叶斯定理之间的关系：
贝叶斯估计使用来进行参数估计的，而贝叶斯定理则是用来进行概率预测的，可通过下面式子进行比较：
贝叶斯估计：P(θ|data) = P(data|θ)*P(θ) / P(data), 其中：
- P(θ)和P(data)都是先验概率；
- P(data|θ)也是似然概率；
- P(θ|data) 则称为后验概率，利用先验（或边缘）P(θ)来估计后验参数。
贝叶斯定理： P(data|θ) = P(θ|data)*P(data) / P(θ)
朴素贝叶斯
初学机器学习可能会觉得上面的式子不太好理解，换个表达式会明朗很多：
又由于p(特征)是特征的全概率，是考虑了所有类别前提下的特征概率，因此对于所有类别的p(类别|特征)，p(特征)都是一样的。
采用更标准的定义：
独立的类别变量C有若干个类别，条件依赖于若干特征变量 F1,F2,F3,...Fn。此时贝叶斯定理就为：
同时，为方便计算，假设所有变量都是相互独立的，且由于分母值都相同，因此上式可转化为：
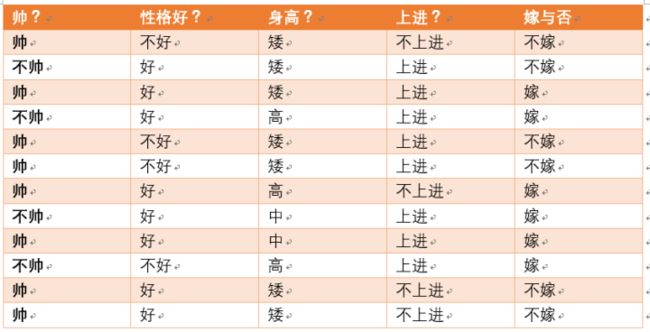
利用朴素贝叶斯进行分类的一个栗子
给定数据如下：
现在给我们的问题是，如果一对男女朋友，男生想女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？
这是一个典型的分类问题，转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率，谁的概率大，我就能给出嫁或者不嫁的答案！
这里我们联系到朴素贝叶斯公式：
由于p(不帅、性格不好、身高矮、不上进)对于p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))都是一样的，因此可以略去分母，只计算分子。
而又由于假设各个特征之间相互独立，因此：
各项概率值的计算过程参见带你理解朴素贝叶斯分类算法。
最后可求得：
p(嫁|(不帅、性格不好、身高矮、不上进))= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)
p (不嫁|不帅、性格不好、身高矮、不上进) = ((1/6*1/2*1*1/2)*1/2)/(1/3*1/3*7/12*1/3)
很显然(1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)。
所以我们根据朴素贝叶斯算法可以给这个女生答案，是不嫁！！！**
拉普拉斯平滑
需注意的是，若某个特征值在训练集中没有与某个类同时出现过，则直接计算该类前提下特征的概率将会出现问题，因为其值将会为0。
为了避免其他属性携带的信息被训练集中未出现的属性值"抹去'，在估计概率值时通常要进行"平滑" (smoothing) ，常用"拉普拉斯修正" (Laplacian correction)。 具体来说，令 N 表示训练集 D 中可能的类别数 ， N; 表示第 i个属性可能的取值数，则p(类别)和p(特征|类别)分别修正为：
参考：
《机器学习》 周志华
从最大似然估计开始，你需要打下的机器学习基石
带你理解朴素贝叶斯分类算法
朴素贝叶斯分类器
贝叶斯定理