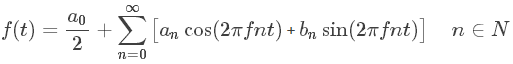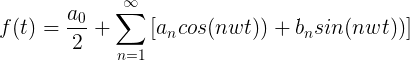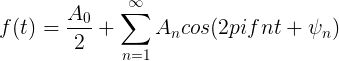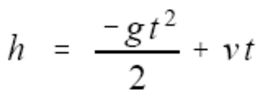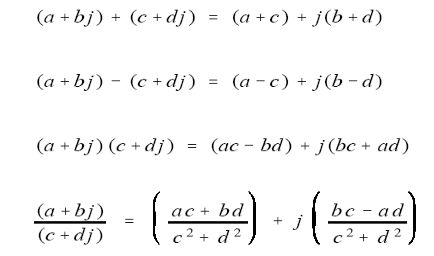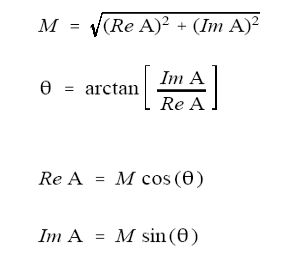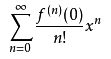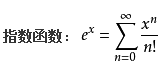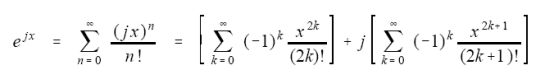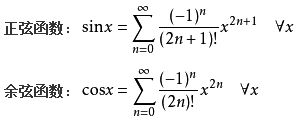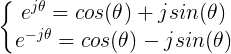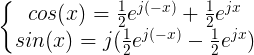说明：
傅里叶级数、傅里叶变换、离散傅里叶变换、短时傅里叶变换。。。这些理解和应用都非常难，网上的文章有两个极端：“Esay” Or “Boring”！如果单独看一两篇文章就弄懂傅里叶，那说明你真的是大神了。
本博文是经过查阅网上几十篇大神的博客、文章、书籍等进行的一个汇总，希望对初学者和我自己一个入门和总结，所以本博文并非原创，抄袭+汇总+修改+总结！
主要参考：
1.傅里叶变换到小波变换的风趣讲解：https://zhuanlan.zhihu.com/p/22450818
2.一篇外文的翻译者，讲的非常好，本博文大部分基于此大神的翻译进行的部分优化：http://blog.csdn.net/dznlong
3.风趣幽默的讲解傅里叶的由来和一些基础：https://zhuanlan.zhihu.com/p/19763358
4.网上很多人都基于这篇外文进行的翻译和总结：http://www.dspguide.com/ch8/5.htm，外文得FQ，这里下载之后供大家下载：
5.扬州大学的一个PPT讲解傅里叶级数推导，原地址不知道在哪，这里给出好心人上传的百度地址：https://wenku.baidu.com/view/67a0cccdda38376baf1faec4.html
6.百度文库关于傅立叶级数到傅立叶变换的详细描述：https://wenku.baidu.com/view/365c63740b4c2e3f57276383.html
7.参考的博文在这里或者博文结尾给出，文中直接引用将不再进行说明，请见谅！
一.风趣理解傅立叶级数
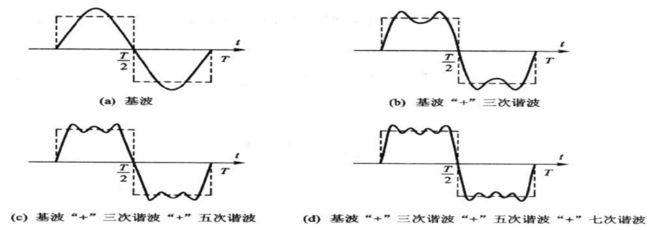
废话先不说，直接看维基百科的几个图片，很容易发现sin(x)和cos(x)可以组合成无穷多种函数，傅立叶级数也是基于此而进行的。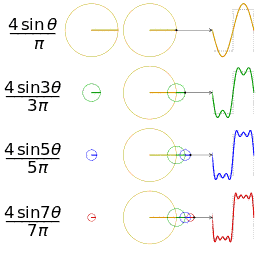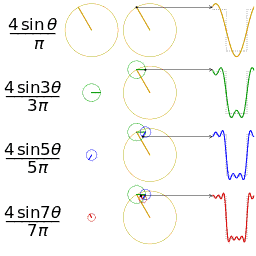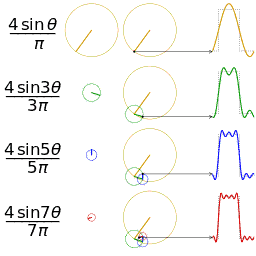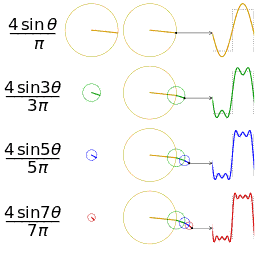
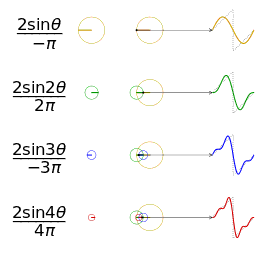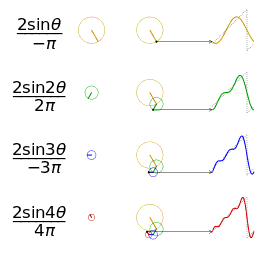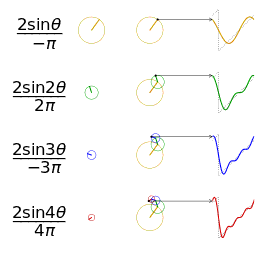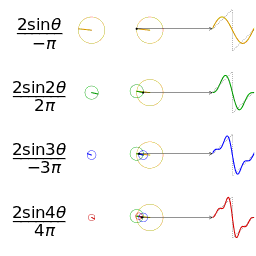
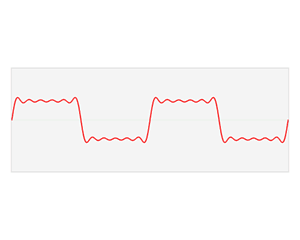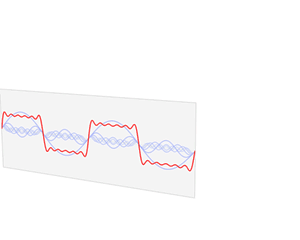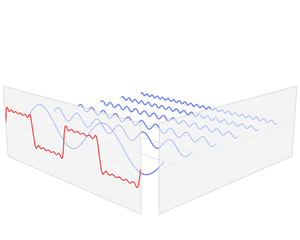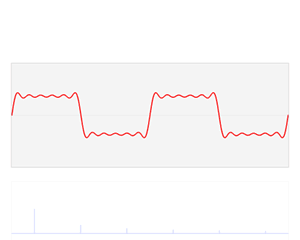是不是直接可以很直观的理解傅立叶的思路？想看具体的推导公式请看下一节~~
二.傅立叶级数的理论理解
2.1函数的正交性
首先明白一个概念，什么叫“正交性”？
我们应该想到向量的正交：如下图所示，
与
正交，在数学上的表达就是点积为0. 
那么我们所有的向量都可以用这个和为基去表示：
由向量的正交性定义，我们引出函数的正交性--->>>
不想手打字了，重复造轮子没意义。
以下是三角函数属于正交函数集的证明：（有时间就了解一下，这个知道就行）
如果想继续了解正交分解多少个N合适，那么请参考“巴塞瓦尔公式”，这里不做详细解释：https://wenku.baidu.com/view/911f5d67ddccda38376baf41.html
2.2傅立叶级数的正余弦形式
好了，有了上面的正交函数的来源，接下来就开始利用Sin(x)和Cos(x)代替一个复杂的函数了。
第一种表示：
上面说了那么多其实就是为了得出傅立叶级数和求解傅立叶参数！
第二种表示：（
）
由以上的推到和分析得到傅立叶级数可表示为如下方程，其中 
表示角频率，周期为T，
表示原始的角度。
我们可以根据三角函数的关系，把上面的式子都换成cos或者sin的样式：
合并之后的另一种表达式如下：
第三种表示：
再由第二种表示傅立叶函数如下所示，角频率，周期T，其它参数见上图！
现在不用角频率去表示，而是用频率f表示函数，大家都知道
，所以得到如下傅立叶公式：
你也许会问，这么多表示方法有什么用？一个物体是不变的，但是从不同的角度分析得有不同的表示方法，便于理解！
2.3复数的含义和欧拉公式
2.3.1复数的提出
在此，先让我们看一个物理实验：把一个球从某点向上抛出，然后根据初速度和时间来计算球所在高度，这个方法可以根据下面的式子计算得出：
其中h表示高度，g表示重力加速度(9.8m/s2)，v表示初速度，t表示时间。现在反过来，假如知道了高度，要求计算到这个高度所需要的时间，这时我们又可以通过下式来计算：
经过计算我们可以知道，当高度是3米时，有两个时间点到达该高度：球向上运动时的时间是0.38秒，球向下运动时的时间是1.62秒。但是如果高度等于10时，结果又是什么呢？根据上面的式子可以发现存在对负数进行开平方运算，我们知道这肯定是不现实的。第一次使用这个不一般的式子的人是意大利数学家Girolamo Cardano（1501-1576），两个世纪后，德国伟大数学家Carl Friedrich Gause（1777-1855）提出了复数的概念，为后来的应用铺平了道路，他对复数进行这样表示：复数由实数（real）和虚数(imaginary)两部分组成，虚数中的根号负1用i来表示（在这里我们用j来表示，因为i在电力学中表示电流的意思）。
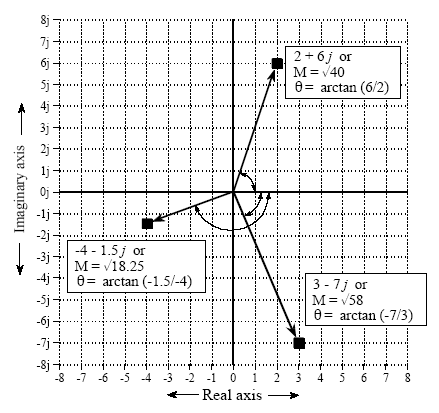
我们可以把横坐标表示成实数，纵坐标表示成虚数，则坐标中的每个点的向量就可以用复数来表示，如下图：
上图中的ABC三个向量可以表示成如下的式子：
A = 2 + 6j
B = -4 – 1.5j
C = 3 – 7j
这样子来表达方便之处在于运用一个符号就能把两个原来难以联系起来的数组合起来了，不方便的是我们要分辨哪个是实数和哪个是虚数，我们一般是用Re( )和Im( )来表示实数和虚数两部分，如：
Re A = 2 Im A = 6
Re B = -4 Im B = -1.5
Re C = 3 Im C = -7
复数之间也可以进行加减乘除运算：
这里有个特殊的地方是j2等于-1，上面第四个式子的计算方法是把分子和分母同时乘以c – dj，这样就可消去分母中的j了。
复数也符合代数运算中的交换律、结合律、分配律：
A B = B A
(A + B) + C = A + (B + C)
A(B + C) = AB + AC
2.3.2复数的极坐标表示形式
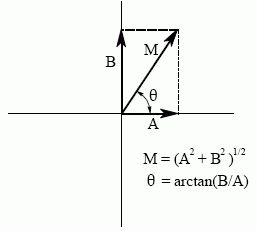
前面提到的是运用直角坐标来表示复数，其实更为普遍应用的是极坐标的表示方法，如下图：
上图中的M即是数量积(magnitude)，表示从原点到坐标点的距离，θ是相位角(phase angle)，表示从X轴正方向到某个向量的夹角，下面四个式子是计算方法：
我们还可以通过下面的式子进行极坐标到直角坐标的转换：
a + jb = M (cosθ + j sinθ)
上面这个等式中左边是直角坐标表达式，右边是极坐标表达式。
2.3.3欧拉公式的引出
还有一个更为重要的等式——欧拉等式（欧拉是瑞士的著名数学家，Leonhard Euler，1707-1783）：
ejx = cos x + j sin x
这个等式可以从下面的泰勒级数变换中得到证明：
泰勒级数在x=0处的展开如下：
指数函数在x=0处的泰勒级数如下：
复数指数函数在x=0处的泰勒展开，再进行分割成sin和cos在x=0处的级数如下：
其中sin(x)、cos(x)的泰勒级数展开如下：
上面中右边的两个式子分别是cos(x)和sin(x)的泰勒(Taylor)级数： ejx = cos x + j sin x
这样子我们又可以把复数的表达式表示成指数的形式了：
a + jb = M e jθ （这便是复数的两个表达式）
指数形式是数字信号处理中数学方法的支柱，也许是因为用指数形式进行复数的乘除运算极为简单的缘故吧：
2.4傅立叶级数的复数表示
由欧拉函数的式子可以推到处sin和cos用指数表示的方程：
转换之后如下所示：
则我们就可以把上面的第二种表示转化为指数的表示：
2.3傅立叶级数的频谱图
注释：想要具体了解特点以及证明为什么收敛等，请看：
这不是我们的重点，想看的朋友也没必要细入--
https://wenku.baidu.com/view/911f5d67ddccda38376baf41.html
https://wenku.baidu.com/view/365c63740b4c2e3f57276383.html
2.3.1频谱图含义
频谱图顾名思义，就是傅立叶级数之后得到的频率和相位图，我们得到这些信息之后肯定想可视化去观察才能得出有用的信息，所以引出这一小节。
咱们还是引用维基百科和网上一位大神的图去体现：
幅度值-频率图：
（由于n>0故称此为单边频谱图）或者 
（由于绝对值里面可正负，所以称为双边频谱图）
相位-频率图 ：
具体求法上一节已经说过了，这里不再赘述！
频率振幅图
时域、频域、相位图
2.3.2傅立叶级数的频谱图特点
三.参考文章
类似我这种参考别人然后一个总结，说的不是很详细：http://blog.csdn.net/znculee/article/details/48291981
一篇外文，大概看了一点点挺好的：https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
文中的公式编辑器：http://www.codecogs.com/latex/eqneditor.php
部分参考博文开头已经给出，如果有参考没有给出地址的，请告知立马改正！