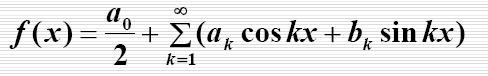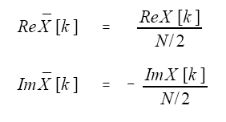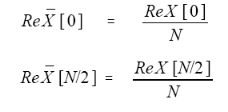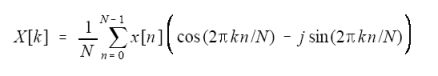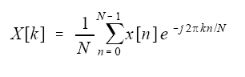说明:
傅里叶级数、傅里叶变换、离散傅里叶变换、短时傅里叶变换。。。这些理解和应用都非常难,网上的文章有两个极端:“Esay” Or “Boring”!如果单独看一两篇文章就弄懂傅里叶,那说明你真的是大神了。
本博文是经过查阅网上几十篇大神的博客、文章、书籍等进行的一个汇总,希望对初学者和我自己一个入门和总结,所以本博文并非原创,抄袭+汇总+修改+总结!
主要参考:
1.傅里叶变换到小波变换的风趣讲解:https://zhuanlan.zhihu.com/p/22450818
2.一篇外文的翻译者,讲的非常好,本博文大部分基于此大神的翻译进行的部分优化:http://blog.csdn.net/dznlong
3.风趣幽默的讲解傅里叶的由来和一些基础:https://zhuanlan.zhihu.com/p/19763358
4.网上很多人都基于这篇外文进行的翻译和总结:http://www.dspguide.com/ch8/5.htm,外文得FQ,这里下载之后供大家下载:
5.扬州大学的一个PPT讲解傅里叶级数推导,原地址不知道在哪,这里给出好心人上传的百度地址:https://wenku.baidu.com/view/67a0cccdda38376baf1faec4.html
6.百度文库关于傅立叶级数到傅立叶变换的详细描述:https://wenku.baidu.com/view/365c63740b4c2e3f57276383.html
7.参考的博文在这里或者博文结尾给出,文中直接引用将不再进行说明,请见谅!
一.离散傅立叶变换的由来
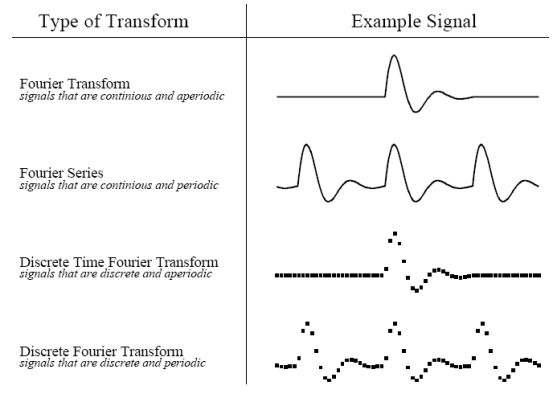
说DFT之前,我们先回忆一下以往的几种傅里叶变换。
从理论上来说,这四种变换已经囊括了我们能遇到的信号种类了,那么为什么要额外引入DFT?从形式上看,DFT与离散时间周期信号的变换非常类似,有何原因?
首先,我们注意到在数字信号处理里面,我们接触的都是离散时间的信号,所以前两种连续时间的傅里叶变换在我们这儿用不到。另外,数字信号处理的一个要点就是讨论对数字信号的处理方式和算法设计,这里所说的处理方式不仅仅是人工的、解析的处理方式,更是机器能用的处理方式。
机器的局限性在哪呢?机器不能表达一个无限长的序列,也不能表达连续的频域特征。对于一般的离散时间信号而言,直接用DTFT确实很好,非常便于我们分析信号的频域特征,但问题是这一套机器是用不了的。因此我们才需要DFT,也就是说DTFT是给人用的,而DFT是给机器用的。
所谓DFT的引入,我认为主要可以分为两点:一点是截断,另一点是(频域)采样。需要截断,是因为机器无法表示无限长的序列,只能处理有限长序列,这一点比较好理解。二是采样,是理解DFT的重点。我们前面提到离散非周期序列的傅里叶变换(DTFT)在频域上是连续的,这连续的频域特征机器是无法表达的,因此我们需要对它进行采样。又由于频域上具有周期性,只需要对2pi长度的区间采样即可。那么应该采多少个点呢?类似于Nyquist采样定理的做法,我们得出采样的点数M≥N即可(N表示该序列的长度),为了方便起见只需取M=N。由此,DFT的两个引入动机就清楚了:它是对无限长序列截断成有限长序列,进行DTFT以后再在频域采样。
那么为何DFT的形式和离散时间周期信号的傅里叶变换形式类似呢?注意到,有限长序列经过周期延拓即可变为周期信号,因此他们之间的相似性也不言而喻了。不过需要注意的是DFT对有限长序列均可以用,但离散时间周期信号的傅里叶变换只能处理周期信号,这是本质的不同。二.离散傅立叶变换的理论及举例
2.1实数形式的傅立叶变换
一个关于实数离散傅立叶变换(Real DFT)的例子
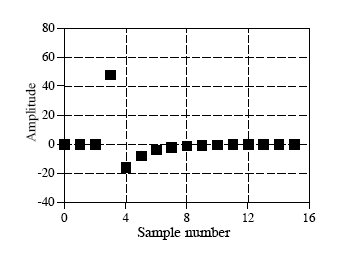
下图是一个原始信号图像:
这个信号的长度是16,于是可以把这个信号分解9个余弦波和9个正弦波(一个长度为N的信号可以分解成![]() 个正余弦信号,这是为什么呢?结合下面的18个正余弦图,我想从计算机处理精度上就不难理解,一个长度为N的信号,最多只能有
个正余弦信号,这是为什么呢?结合下面的18个正余弦图,我想从计算机处理精度上就不难理解,一个长度为N的信号,最多只能有 ![]() 个不同频率,再多的频率就超过了计算机所能所处理的精度范围),如下图:
个不同频率,再多的频率就超过了计算机所能所处理的精度范围),如下图:
首先我们这样的做法是为了保证精度,那么既然是保证精度也就是我们得找到最小的采样次数m正好满足正常的精度要求,现在问题就转化为我们采样的次数问题了。
采样次数[1,N-1],其中sin和cos是对应的,那么总采样就是[1,2N]。
我们再次想一下,sin和cos都是周期函数,假设周期是T,那么每个周期的采样[1,![]() ],在每个周期里采样最少多少次才能确定一个sin或者cos呢?,
],在每个周期里采样最少多少次才能确定一个sin或者cos呢?,
看下面的sin函数的参数:
![]()
可以看到有三个参数A、w、![]() .
.
那么就需要最少三个参数要解这个方程,或者说至少三个点来描述这个函数走向。
现在知道一个周期最少需要三个点,那么一个函数整个周期需要[3T,N/T],但是有一个问题,两个周期之间可以共用一个点,那么我们就可以减少采样点的个数了,需要的是最小的采样点,那就是2T个点,当然最后还得补1。
别忘了一个问题,这是离散的时间信号,离散什么意思?离散:1,2,3.。。。连续:1,1.001,1.002.。。。,那么我们知道采样点只能取整数了,当然这是便于计算机计算的一种方式吧!
现在得到一个周期T内至少采样2个点,那么N个采样点中,最大的周期就是![]() .
.
现在以实际数字计算,N=16,每个周期需至少需要2个采样点,那么周期T最大是8.别忘了一点,还有个不是sin和cos的基数,y=k,再加上这个特殊的基函数,那么就是9个。也就是我们的公式![]() .
.
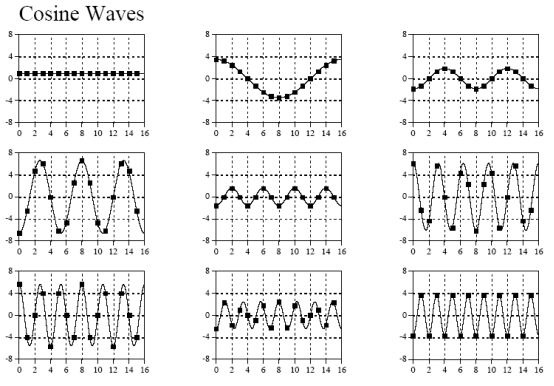
9个余弦信号:
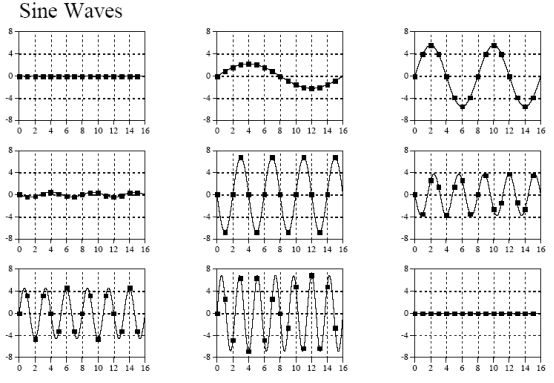
9个正弦信号:
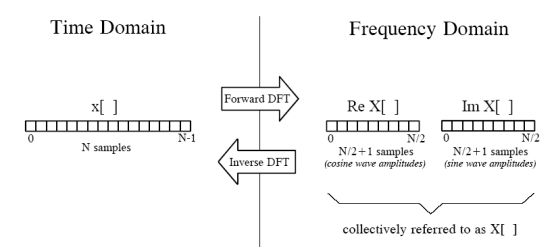
把以上所有信号相加即可得到原始信号,至于是怎么分别变换出9种不同频率信号的,我们先不急,先看看对于以上的变换结果,在程序中又是该怎么表示的,我们可以看看下面这个示例图:
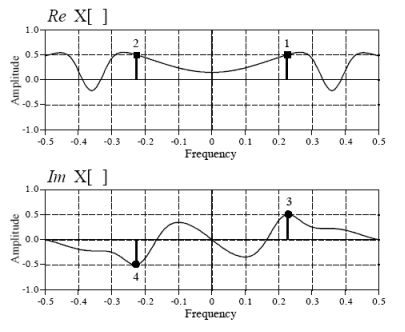
上图中左边表示时域中的信号,右边是频域信号表示方法,从左向右表示正向转换(Forward DFT),从右向左表示逆向转换(Inverse DFT),用小写x[]表示信号在每个时间点上的幅度值数组, 用大写X[]表示每种频率的副度值数组, 因为有![]() 种频率,所以该数组长度为
种频率,所以该数组长度为![]() ,X[]数组又分两种,一种是表示余弦波的不同频率幅度值:Re X[],另一种是表示正弦波的不同频率幅度值:Im X[],Re是实数(Real)的意思,Im是虚数(Imagine)的意思,采用复数的表示方法把正余弦波组合起来进行表示,但这里我们不考虑复数的其它作用,只记住是一种组合方法而已,目的是为了便于表达(在后面我们会知道,复数形式的傅立叶变换长度是N,而不是
,X[]数组又分两种,一种是表示余弦波的不同频率幅度值:Re X[],另一种是表示正弦波的不同频率幅度值:Im X[],Re是实数(Real)的意思,Im是虚数(Imagine)的意思,采用复数的表示方法把正余弦波组合起来进行表示,但这里我们不考虑复数的其它作用,只记住是一种组合方法而已,目的是为了便于表达(在后面我们会知道,复数形式的傅立叶变换长度是N,而不是![]() )。
)。
DFT基本函数
ck[i] = cos(2πki/N)
sk[i] = sin(2πki/N)
其中k表示每个正余弦波的频率,如为2表示在0到N长度中存在两个完整的周期,10即有10个周期,如下图:
上图中至于每个波的振幅(amplitude)值(Re X[k],Im X[k])是怎么算出来的,这个是DFT的核心,也是最难理解的部分,我们先来看看如何把分解出来的正余弦波合成原始信号(Inverse DFT)。
合成运算方法(Real Inverse DFT)
DFT合成等式:
如果有学过傅立叶级数,对这个等式就会有似曾相识的感觉,不错!这个等式跟傅立叶级数是非常相似的:
当然,差别是肯定是存在的,因为这两个等式是在两个不同条件下运用的,至于怎么证明DFT合成公式,这个我想需要非常强的高等数学理论知识了,这是研究数学的人的工作,对于普通应用者就不需要如此的追根究底了,但是傅立叶级数是好理解的,我们起码可以从傅立叶级数公式中看出DFT合成公式的合理性。
DFT合成等式中的Im [k]和Re [k]跟Im X[k]和Re X[k]是不一样的,下面是转换方法:
但k等于0和N/2时,实数部分的计算要用下面的等式:
上面四个式中的N是时域中点的总数,k是从0到N/2的序号。
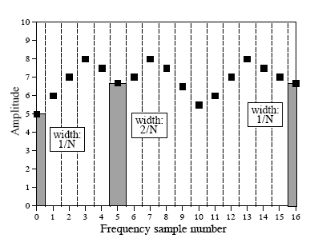
为什么要这样进行转换呢?这个可以从频谱密度(spectral density)得到理解,如下图就是个频谱图:
这是一个频谱图,横坐标表示频率大小,纵坐标表示振幅大小,原始信号长度为N(这里是32),经DFT转换后得到的17个频率的频谱,频谱密度表示每单位带宽中为多大的振幅,那么带宽是怎么计算出来的呢?看上图,除了头尾两个,其余点的所占的宽度是2/N,这个宽度便是每个点的带宽,头尾两个点的带宽是1/N,而Im X[k]和Re X[k]表示的是频谱密度,即每一个单位带宽的 振幅大小,但Im [k]和Re [k]表示2/N(或1/N)带宽的振幅大小,所以Im [k]和Re [k]分别应当是Im X[k]和Re X[k]的2/N(或1/N)。
频谱密度就象物理中物质密度,原始信号中的每一个点就象是一个混合物,这个混合物是由不同密度的物质组成的,混合物中含有的每种物质的质量是一样的,除了最大和最小两个密度的物质外,这样我们只要把每种物质的密度加起来就可以得到该混合物的密度了,又该混合物的质量是单位质量,所以得到的密度值跟该混合物的质量值是一样的。
至于为什么虚数部分是负数,这是为了跟复数DFT保持一致,这个我们将在后面会知道这是数学计算上的需要(Im X[k]计算时加上了一个负号,Im [k]再加上负号,结果便是正的,等于没有变化)。
分解运算方法(DFT)
有三种完全不同的方法进行DFT:一种方法是通过联立方程进行求解, 从代数的角度看,要从N个已知值求N个未知值,需要N个联立方程,且N个联立方程必须是线性独立的,但这是这种方法计算量非常的大且极其复杂,所以很少被采用;第二种方法是利用信号的相关性(correlation)进行计算,这个是我们后面将要介绍的方法;第三种方法是快速傅立叶变换(FFT),这是一个非常具有创造性和革命性的的方法,因为它大大提高了运算速度,使得傅立叶变换能够在计算机中被广泛应用,但这种算法是根据复数形式的傅立叶变换来实现的,它把N个点的信号分解成长度为N的频域,这个跟我们现在所进行的实域DFT变换不一样,而且这种方法也较难理解,这里我们先不去理解,等先理解了复数DFT后,再来看一下FFT。有一点很重要,那就是这三种方法所得的变换结果是一样的,经过实践证明,当频域长度为32时,利用相关性方法进行计算效率最好,否则FFT算法效率较高。现在就让我们来看一下相关性算法。
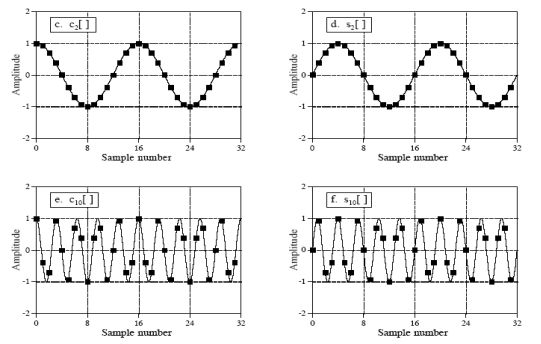
利用信号的相关性(correlation)可以从噪声背景中检测出已知的信号,我们也可以利用这个方法检测信号波中是否含有某个频率的信号波:把一个待检测信号波乘以另一个信号波,得到一个新的信号波,再把这个新的信号波所有的点进行相加,从相加的结果就可以判断出这两个信号的相似程度。如下图:
上面a和 b两个图是待检测信号波,图a很明显可以看出是个3个周期的正弦信号波,图b的信号波则看不出是否含有正弦或余弦信号,图c和d都是个3个周期的正弦信号波,图e和f分别是a、b两图跟c、d两图相乘后的结果,图e所有点的平均值是0.5,说明信号a含有振幅为1的正弦信号c,但图f所有点的平均值是0,则说明信号b不含有信号d。这个就是通过信号相关性来检测是否含有某个信号的方法。
相应地,我也可以通过把输入信号和每一种频率的正余弦信号进行相乘(关联操作),从而得到原始信号与每种频率的关联程度(即总和大小),这个结果便是我们所要的傅立叶变换结果,下面两个等式便是我们所要的计算方法:
第二个式子中加了个负号,是为了保持复数形式的一致,前面我们知道在计算Im [k]时又加了个负号,所以这只是个形式的问题,并没有实际意义,你也可以把负号去掉,并在计算Im [k]时也不加负号。
这里有一点必须明白一个正交的概念:两个函数相乘,如果结果中的每个点的总和为0,则可认为这两个函数为正交函数。要确保关联性算法是正确的,则必须使得跟原始信号相乘的信号的函数形式是正交的,我们知道所有的正弦或余弦函数是正交的,这一点我们可以通过简单的高数知识就可以证明它,所以我们可以通过关联的方法把原始信号分离出正余弦信号。当然,其它的正交函数也是存在的,如:方波、三角波等形式的脉冲信号,所以原始信号也可被分解成这些信号,但这只是说可以这样做,却是没有用的。
2.2复数形式的傅立叶变换
把变换前后都看成复数的形式
复数形式傅立叶变换成原始信号x[n]当成是一个用复数来表示的信号,其中实数部分表示原始信号值,虚数部分为0,变换结果X[k]也是个复数的形式,但这里的虚数部分是有值的。在这里用复数的观点来看原始信号非常的关键,是理解复数形式傅立叶变换的关键(如果有学过复变函数则可能更好理解,即把x[n]看成是一个复数变量,然后象对等实数那样对这个复数变量进行相同的变换)。
对复数进行相关性算法(正向傅立叶变换)
从实数傅立叶变换中可以知道,我们可以通过原始信号把乘以一个正交函数形式的信号,然后进行求总和,最后就能得到这个原始信号所包含的正交函数信号的分量。现在我们的原始信号变成了复数,我们要得到的是复数的信号分量,我们是不是可以把它乘以一个复数形式的正交函数呢?答案是肯定的,正余弦函数都是正交函数,变成如下形式的复数后,仍旧还是正交函数(这个从正交函数的定义可以很容易得到证明):
cos x + j sin x, cos x – j sin x,……
这里我采用上面的第二个式子进行相关性求和,为什么用第二个式,我在后面会知道,正弦函数在虚数中变换后得到的是负的正弦函数,这里我们再加上一个负号,使得最后的得到的是正的正弦波,根据这个于是我们很容易就可以得到了复数形式的DFT正向变换等式:
这个式子很容易可以得到欧拉变换式子:
其实我们是为了表过上的方便才用到欧拉变换式,在分析问题是我们还是较多地用到正余弦表达式。
对于上面的等式,我们要清楚如下几个方面(也是区别于实数DFT的地方):
1、 X[k]、x[n]都是复数,但x[n]的虚数部分都是由0组成的,实数部分表示原始信号;
2、 k的取值范围是0 ~ N-1 (也可以表达成0 ~ 2π),其中0 ~ N/2(或0 ~ π)是正频部分,N/2 ~ N-1(π~ 2π)是负频部分,由于正余弦函数的对称性,所以我们把 –π~ 0表示成π~ 2π,这是出于计算上方便的考虑。
3、 其中的j是一个不可分离的组成部分,就象一个等式中的变量一样,不能随便去掉,去掉之后意义就完全不一样了,但我们知道在实数DFT中,j只是个符号而已,把j去掉,整个等式的意义不变;
4、 下图是个连续信号的频谱,但离散频谱也是与此类似的:
上面的频谱图把负频率放到了左边,是为了迎合我们的思维习惯,但在实际实现中我们一般是把它移到正的频谱后面的。
从上图可以看出,时域中的正余弦波(用来组成原始信号的正余弦波)在复数DFT的频谱中被分成了正、负频率的两个组成部分,基于此等式中前面的比例系数是1/N(或1/2π),而不是2/N,这是因为现在把频谱延伸到了2π,但把正负两个频率相加即又得到了2/N,又还原到了实数DFT的形式,这个在后面的描述中可以更清楚地看到。由于复数DFT生成的是一个完整的频谱,原始信号中的每一个点都是由正、负两个频率组合而成的,所以频谱中每一个点的带宽是一样的,都是1/N,相对实数DFT,两端带宽比其它点的带宽少了一半;
复数DFT的频谱特征具有周期性:-N/2 ~ 0与N/2 ~ N-1是一样的,实域频谱呈偶对称性(表示余弦波频谱),虚域频谱呈奇对称性(表示正弦波频谱)。
逆向傅立叶变换
假设我们已经得到了复数形式的频谱X[k],现在要把它还原到复数形式的原始信号x[n],当然应该是把X[k]乘以一个复数,然后再进行求和,最后得到原始信号x[n],这个跟X[k]相乘的复数首先让我们想到的应该是上面进行相关性计算的复数:cos(2πkn/N) – j sin(2πkn/N),但其中的负号其实是为了使得进行逆向傅立叶变换时的正弦函数变为正的符号,因为虚数j的运算特殊性,使得原来应该是正的正弦函数变为了负的正弦函数(我们后面的推导会看到这一点),所以这里的负号只是为了纠正符号的作用,在进行逆向DFT时,我们可以把负号去掉,于是我们便得到了这样的逆向DFT变换等式:
x[n] = X[k] (cos(2πkn/N) + j sin(2πkn/N))
我们现在来分析这个式子,会发现这个式其实跟实数傅立叶变换是可以得到一样结果的。我们先把X[k]变换一下:
X[k] = Re X[k] + j Im X[k]
这样我们就可以对x[n]再次进行变换,如:
x[n] = (Re X[k] + j Im X[k]) (cos(2πkn/N) + j sin(2πkn/N))
= ( Re X[k] cos(2πkn/N) + j Im X[k] cos(2πkn/N) +
j Re X[k] sin(2πkn/N) - Im X[k] sin(2πkn/N) )
= ( Re X[k] (cos(2πkn/N) + j sin(2πkn/N)) + ---------------------(1)
Im X[k] ( - sin(2πkn/N) + j cos(2πkn/N))) ---------------(2)
这时我们就把原来的等式分成了两个部分,第一个部分是跟实域中的频谱相乘,第二个部分是跟虚域中的频谱相乘,根据频谱图我们可以知道,Re X[k]是个偶对称的变量,Im X[k]是个奇对称的变量,即
Re X[k] = Re X[- k]
Im X[k] = - Im X[-k]
但k的范围是0 ~ N-1,0~N/2表示正频率,N/2~N-1表示负频率,为了表达方便我们把N/2~N-1用-k来表示,这样在从0到N-1的求和过程中对于(1)和(2)式分别有N/2对的k和-k的和,对于(1)式有:
Re X[k] (cos(2πkn/N) + j sin(2πkn/N)) + Re X[- k] (cos( - 2πkn/N) + j sin( -2πkn/N))
根据偶对称性和三角函数的性质,把上式化简得到:
Re X[k] (cos(2πkn/N) + j sin(2πkn/N)) + Re X[ k] (cos( 2πkn/N) - j sin( 2πkn/N))
这个式最后的结果是:
2 Re X[ k] cos(2πkn/N)
再考虑到求Re X[ k]等式中有个1/N,把1/N乘以2,这样的结果不就是跟实数DFT中的式子一样了吗?
对于(2)式,用同样的方法,我们也可以得到这样的结果:
-2 Im X[k] sin(2πkn/N)
注意上式前面多了个负符号,这是由于虚数变换的特殊性造成的,当然我们肯定不能把负符号的正弦函数跟余弦来相加,还好,我们前面是用cos(2πkn/N) – j sin(2πkn/N)进行相关性计算,得到的Im X[k]前面有个负的符号,这样最后的结果中正弦函数就没有负的符号了,这就是为什么在进行相关性计算时虚数部分要用到负符号的原因(我觉得这也许是复数形式DFT美中不足的地方,让人有一种拼凑的感觉)。
从上面的分析中可以看出,实数傅立叶变换跟复数傅立叶变换,在进行逆变换时得到的结果是一样的,只不过是殊途同归吧。
三.参考文章
类似我这种参考别人然后一个总结,说的不是很详细:http://blog.csdn.net/znculee/article/details/48291981
一篇外文,大概看了一点点挺好的:https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
文中的公式编辑器:http://www.codecogs.com/latex/eqneditor.php
离散傅里叶变换的由来介绍:https://www.zhihu.com/question/21314374?answer_deleted_redirect=true
离散傅立叶中N/2+1的由来理解:http://blog.csdn.net/u011583927/article/details/45934455
部分参考博文开头已经给出,如果有参考没有给出地址的,请告知立马改正!