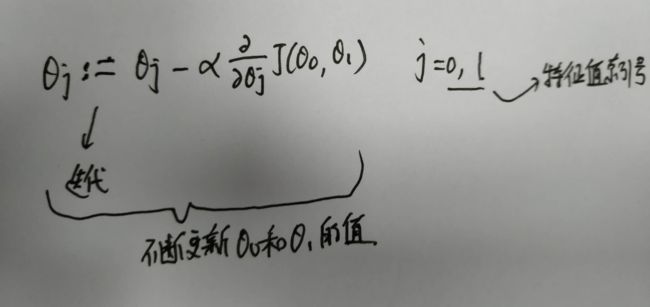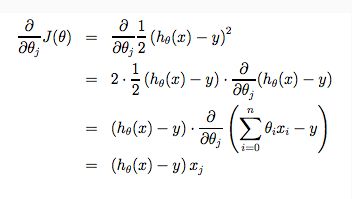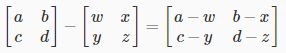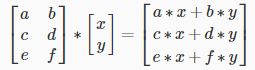吴恩达机器学习知识点回归和课后习题练习(week 1)

week 1

什么是机器学习？

它包含两个定义：
1.较老的，非正式的定义："the field of study that gives computers the ability to learn without being explicitly programmed."
2.一个更现代的定义： "A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E."

通常，任何机器学习问题都可以分配到两个广泛的分类之一：
监督学习和无监督学习

什么是监督学习

在有监督的学习中，我们得到一个数据集，并且已经知道我们的正确输出应该是什么样的，并且认为输入和输出之间存在关系。

监督学习问题分为“回归”和“分类”问题。

1.在回归问题中，我们试图在连续输出中预测结果，这意味着我们正在尝试将输入变量映射到某个连续函数。
2.在分类问题中，我们试图在离散输出中预测结果。换句话说，我们正在尝试将输入变量映射到离散类别。

解析：
给出房地产市场房屋面积的数据，请尝试预测房价。
给出房地产市场房屋面积的数据，请尝试预测房子“卖得多于还是低于要价”。
这是两种不同的类别。

什么是无监督学习？

无监督学习使我们能够在很少或根本不知道我们的结果应该是什么样的情况下处理问题。我们可以从数据中导出结构，我们不一定知道变量的影响。我们可以通过基于数据中变量之间的关系对数据进行聚类来推导出这种结构。在无监督学习的情况下，没有基于预测结果的反馈。

鸡尾酒会问题和基因自动分组。

模型表示

为了建立未来使用的符号，我们定义了输入变量（输入要素）x(i)、试图预测的“输出”或目标变量y(i)、训练示例(x(i),y(i)) 、数据集(x(i),y(i));i=1,...,m

请注意，符号中的上标“(i)”只是训练集的索引，与取幂无关。
我们还将使用X来表示输入值的空间，并使用Y来表示输出值的空间。

为了更加正式地描述监督学习问题，我们的目标是，在给定训练集的情况下，学习函数h：X→Y，使得h(x)是y的对应值的“好”预测器。由于历史原因，该函数h被称为假设。从图中可以看出，这个过程是这样的：

当我们试图预测的目标变量是连续的时，例如在我们的住房示例中，我们将学习问题称为回归问题。当y只能承受少量离散值时（例如，如果给定生活区域，我们想要预测住宅是房屋还是公寓），我们将其称为分类问题。

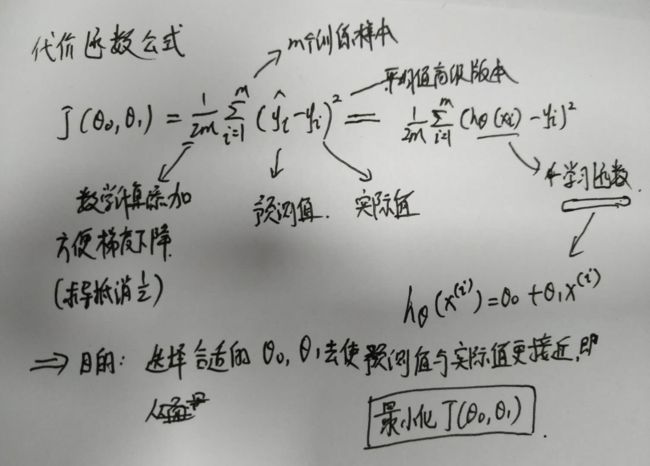
代价函数
我们可以使用代价函数来衡量我们的假设函数的准确性。这需要假设的所有结果与来自x和实际输出y的输入的平均差异（实际上是平均值的更高版本）。

如果把代价函数通过几何进行表述：训练数据集分散在x-y平面上。我们正在努力做一条直线，使它通过这些分散的数据点。

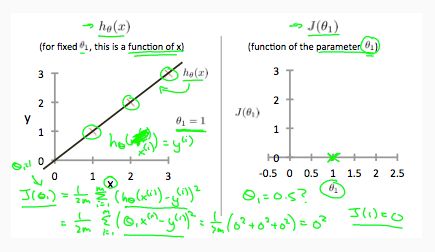
1.代价函数描述（一）
对于一个简单的模型（θ0 = 0）描述：

当θ1 = 1时，我们得到的斜率为1，它遍历模型中的每个数据点。当θ1 = 0.5时，发现从我们的拟合到数据点的垂直距离增加。

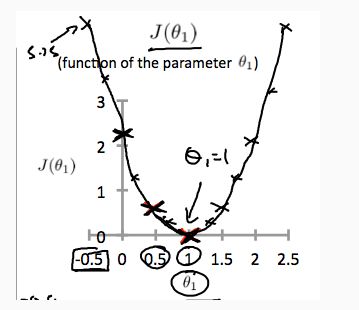
绘制其他几个点会产生如下图（J(θ1)函数图）：

因此，为了最小化代价函数，应该选取θ1 = 1。

2.代价函数解释（二）
对于θ0 != 0的情况：

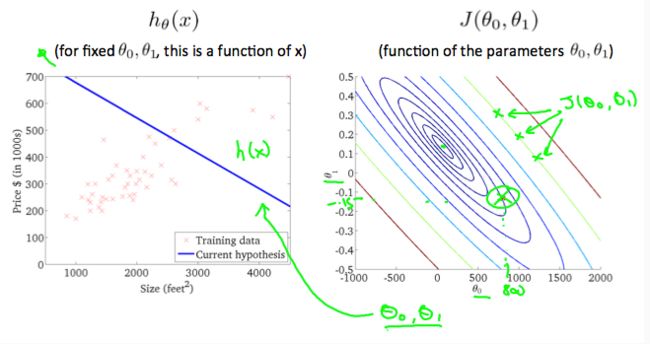
首先，用等高线图（双变量函数的轮廓线在同一行的所有点处具有恒定值）描述二维模型。

沿着'圆'得到的是相同的代价函数值 J(θ0,θ1)，例如，上面绿线上的三个绿点具有相同的值。取另一个h(x)并绘制其等高线图，可得到以下图表：

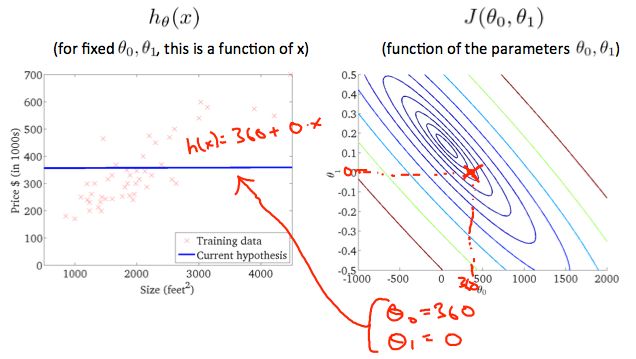
当θ0 = 360，θ1 = 0，得到的新图标在等高线图中靠近中心，减少了成本函数误差。下面给出假设函数可以正好地拟合数据图。

上图最小化了代价函数，此时θ0 = 250，θ1 = 0.12，在我们的图表右侧绘制这些值似乎将我们的观点置于最内圈“圆圈”的中心。

梯度下降

所以我们有假设函数，我们有一种方法可以衡量它与数据的匹配程度。现在我们需要估计假设函数中的参数。这就是梯度下降的地方。

我们不是绘制x和y本身，而是我们的假设函数的参数范围以及选择一组特定参数所产生的代价。

我们把0θ画在x轴、θ1画在y轴上，在垂直z轴上表示代价函数。我们的图上的点将是代价函数的结果，使用我们的假设和那些特定的θ参数。

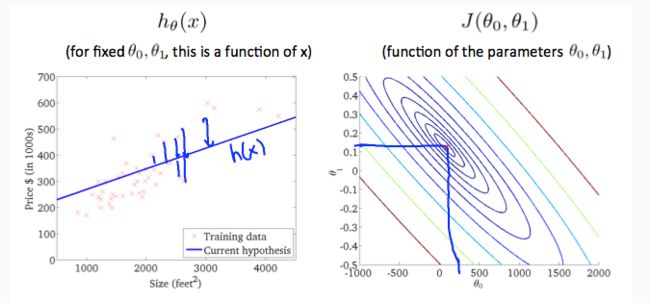
当我们的代价函数位于图中凹坑的最底部时，即当它的值最小时，我们就知道我们已经成功了。红色箭头显示图表中的最小点。

我们这样做的方法是采用我们的代价函数的导数（一个函数的切线）。切线的斜率是该点的导数，它将为我们提供朝向的方向。我们在最陡下降的方向上降低成本函数。每个步骤的大小由参数α确定，该参数称为学习率。例如，上图中每个“星”之间的距离表示由参数α确定的步长。较小的α将导致较小的步长，较大的α将导致较大的步长。采取步骤的方向由J(θ0, θ1)的偏导数确定。根据图表的开始位置，可能会在不同的点上结束。上图显示了两个不同的起点，最终出现在两个不同的地方。

梯度下降算法是：

重复直到收敛

注意：在每次迭代j中，应该同时更新参数θ0, θ1...θn，在第j次迭代计算另一个参数之前更新特定参数将导致错误的实现。

梯度下降

我们现在令θ0 = 0，只使用一个参数θ1，绘制其代价函数以实现梯度下降。单个参数公式是：

无论偏导数的大小，即斜率正负，θ1最终都将收敛到最小值。

另外，我们应该调整参数α以确保梯度下降算法在合理的时间内收敛。 没有收敛或太多时间来获得最小值意味着我们的步长是错误的。

参数α过小将导致收敛缓慢。过大将导致无法收敛（发散）。

为什么最终会收敛？

当我们接近凸函数的底部时，偏导数（斜率）变成0，从而得到：

即随着梯度下降的不断进行，学习速率α（偏导项）会自动变小，所以迭代过程中不需要调整参数α。

线性回归的梯度下降

当特别应用于线性回归的情况时，可以导出梯度下降方程的新形式。我们可以替换我们的实际代价函数和我们的实际假设函数，并将等式修改为（求偏导）：

求偏导过程（推导）：

所有这一切的要点是，如果我们开始猜测我们的假设，然后重复应用这些梯度下降方程，我们的假设将变得越来越准确。

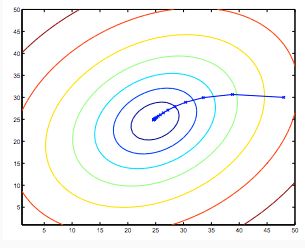
因此，这只是原始代价函数J的梯度下降。该方法在每个步骤中查看整个训练集中的每个示例，并称为*批量梯度下降。 请注意，虽然梯度下降一般易受局部最小值的影响，但我们在线性回归中提出的优化问题只有一个全局，而没有其他局部最优。因此，梯度下降总是收敛（假设学习率α不是太大）到全局最小值。实际上，J是凸二次函数。下面是梯度下降的示例，因为它是为了最小化 二次函数而运行的。

上面显示的椭圆是二次函数的轮廓。 还示出了梯度下降所采用的轨迹，其在（48,30）处初始化。图中的x（由直线连接）标记了当它收敛到其最小值过程中渐变下降经历的连续值θ。

矩阵和向量

矩阵是二维数组；向量是一个包含一列和多行的矩阵，因此，向量是矩阵的子集。

符号和术语：
1.Aij指矩阵A的第i行和第j列中的元素。
2.具有'n'行的向量被称为'n'维向量。
3.vi指向量的第i行中的元素。
4.通常，我们所有的向量和矩阵都是1索引的。请注意，对于某些编程语言，数组是0索引的。
5.矩阵通常用大写名称表示，而向量是小写。
6.“标量”表示对象是单个值，而不是向量或矩阵。
7.R是指一组标量实数。
8.Rn指实数的n维向量集。
9.运行下面的单元格以熟悉Octave / Matlab中的命令。随意创建矩阵和向量，并尝试不同的东西。

% The ; denotes we are going back to a new row.
A = [1, 2, 3; 4, 5, 6; 7, 8, 9; 10, 11, 12]

% Initialize a vector 
v = [1;2;3] 

% Get the dimension of the matrix A where m = rows and n = columns
[m,n] = size(A)

% You could also store it this way
dim_A = size(A)

% Get the dimension of the vector v 
dim_v = size(v)

% Now let's index into the 2nd row 3rd column of matrix A
A_23 = A(2,3)