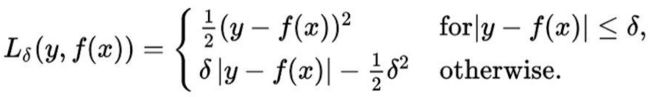tensorflow for research 学习笔记3

TensorFlow中的Linear Regression

线性回归是机器学习中非常简单的问题，我们用tensorflow实现一个小例子。

问题: 希望能够找到一个城市中纵火案和盗窃案之间的关系，纵火案的数量是X，盗窃案的数量是Y，我们建设存在如下线性关系，Y = wX + b。

TensorFlow实现

首先定义输入X和目标Y的占位符(placeholder)

X = tf.placeholder(tf.float32, shape=[], name='input')
Y = tf.placeholder(tf.float32, shape=[], name='label')

里面shape=[]表示标量(scalar)

然后定义需要更新和学习的参数w和b

w = tf.get_variable(
    'weight', shape=[], initializer=tf.truncated_normal_initializer())
b = tf.get_variable('bias', shape=[], initializer=tf.zeros_initializer())

接着定义好模型的输出以及误差函数，这里使用均方误差(Y - Y_predicted)^2

Y_predicted = w * X + b
loss = tf.square(Y - Y_predicted, name='loss')

然后定义好优化函数，这里使用最简单的梯度下降，这里的学习率不仅可以是常量，还可以是一个tensor

optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-3).minimize(loss)

tensorflow是如何判断哪些参数该更新，哪些参数不更新呢？tf.Variabel(trainable=False)就表示不对该参数进行更新，默认下tf.Variable(trainable=True)。

然后在session中做运算

init = tf.global_variables_initializer()
with tf.Session() as sess:
    writer = tf.summary.FileWriter('./linear_log', graph=sess.graph)
    sess.run(init)
    for i in range(100):
        total_loss = 0
        for x, y in data:
            _, l = sess.run([optimizer, h_loss], feed_dict={X: x, Y: y})
            total_loss += l
        print("Epoch {0}: {1}".format(i, total_loss / n_samples))

可视化

我们可以打开tensorboard查看我们的结构图如下

Paste_Image.png

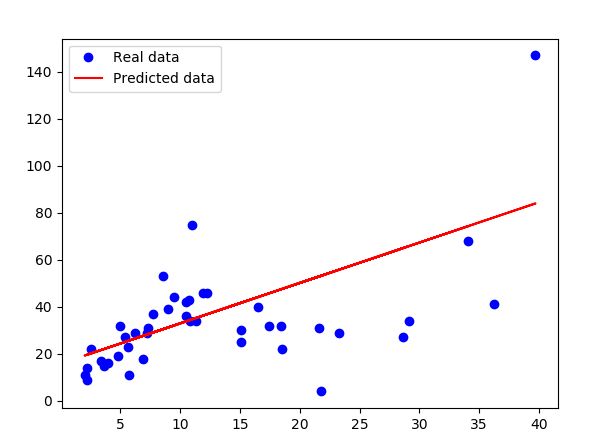
最后我们将数据点和预测的直线画出来

Paste_Image.png

如何改善模型

1. 我们可以增加维度，原始模型是Y = Xw + b，我们可以提升一维，使其变成Y = X^2 w1 + X w2 + b

2. 可以换一种loss的计算方式，比如huber loss，当误差比较小的时候使用均方误差，误差比较大的时候使用绝对值误差

Paste_Image.png

在实现huber loss的时候，因为tf是以图的形式来定义，所以不能使用逻辑语句，比如if等，我们可以使用TensorFlow中的条件判断语句，比如tf.where、tf.case等等，huber loss的实现方法如下

def huber_loss(labels, predictions, delta=1.0):
    residual = tf.abs(predictions - labels)
    condition = tf.less(residual, delta)
    small_res = 0.5 * residual**2
    large_res = delta * residual - 0.5 * delta**2
    return tf.where(condition, small_res, large_res)

关于Optimizer

TensorFlow会自动求导，然后更新参数，使用一行代码tf.train.GradientDescentOptimizer(learning_rate=1e-3).minimize(loss)，下面我们将其细分开来，讲一讲每一步。

自动梯度

首先优化函数的定义就是前面一部分opt = tf.train.GradientDescentOptimizer(learning_rate)，定义好优化函数之后，可以通过grads_and_vars = opt.compute_gradients(loss, )来计算loss对于一个变量列表里面每一个变量的梯度，得到的grads_and_vars是一个list of tuples，list中的每个tuple都是由(gradient, variable)构成的，我们可以通过get_grads_and_vars = [(gv[0], gv[1]) for gv in grads_and_vars]将其分别取出来，然后通过opt.apply_gradients(get_grads_and_vars)来更新里面的参数，下面我们举一个小例子。

import tensorflow as tf

x = tf.Variable(5, dtype=tf.float32)
y = tf.Variable(3, dtype=tf.float32)

z = x**2 + x * y + 3

sess = tf.Session()
# initialize variable
sess.run(tf.global_variables_initializer())

# define optimizer
optimizer = tf.train.GradientDescentOptimizer(0.1)

# compute gradient z w.r.t x and y
grads_and_vars = optimizer.compute_gradients(z, [x, y])

# fetch the variable
get_grads_and_vars = [(gv[0], gv[1]) for gv in grads_and_vars]

# dz/dx = 2*x + y= 13
# dz/dy = x = 5
print('grads and variables')
print('x: grad {}, value {}'.format(
    sess.run(get_grads_and_vars[0][0]), sess.run(get_grads_and_vars[0][1])))

print('y: grad {}, value {}'.format(
    sess.run(get_grads_and_vars[1][0]), sess.run(get_grads_and_vars[1][1])))

print('Before optimization')
print('x: {}, y: {}'.format(sess.run(x), sess.run(y)))

# optimize parameters
opt = optimizer.apply_gradients(get_grads_and_vars)
# x = x - 0.1 * dz/dx = 5 - 0.1 * 13 = 3.7
# y = y - 0.1 * dz/dy = 3 - 0.1 * 5 = 2.5
print('After optimization using learning rate 0.1')
sess.run(opt)
print('x: {:.3f}, y: {:.3f}'.format(sess.run(x), sess.run(y)))
sess.close()

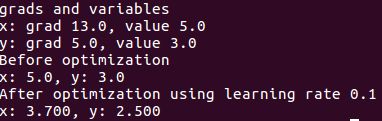
上面程序的注释已经解释了所有的内容，就不细讲了，最后可以得到下面的结果。

Paste_Image.png

在实际中，我们当然不用手动更新参数，optimizer类可以帮我们自动更新，另外还有一个函数也能够计算梯度。

tf.gradients(ys, xs, grad_ys=None, name='gradients',  colocate_gradients_with_ops=False, gate_gradients=False,
aggregation_method=None)

这个函数会返回list，list的长度就是xs的长度，list中每个元素都是$sum_{ys}(dys/dx)$。

实际运用： 这个方法对于只训练部分网络非常有用，我们能够使用上面的函数只对网络中一部分参数求梯度，然后对他们进行梯度的更新。

优化函数类型

随机梯度下降(GradientDescentOptimizer)仅仅只是tensorflow中一个小的更新方法，下面是tensorflow目前支持的更新方法的总结

tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.ProximalGradientDescentOptimizer
tf.train.ProximalAdagradOptimizer
tf.train.RMSPropOptimizer

这个博客对上面的方法都做了介绍，感兴趣的同学可以去看看，另外cs231n和coursera的神经网络课程也对各种优化算法做了介绍。

TensorFlow 中的Logistic Regression

我们使用简单的logistic regression来解决分类问题，使用MNIST手写字体，我们的模型公式如下

$$
logits = X * w + b
$$
$$
Y_{predicted} = softmax(logits)
$$
$$
loss = CrossEntropy(Y, Y_{predicted})
$$

TensorFlow实现

TF Learn中内置了一个脚本可以读取MNIST数据集

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('./data/mnist', one_hot=True)

接着定义占位符(placeholder)和权重参数

x = tf.placeholder(tf.float32, shape=[None, 784], name='image')
y = tf.placeholder(tf.int32, shape=[None, 10], name='label')

w = tf.get_variable(
    'weight', shape=[784, 10], initializer=tf.truncated_normal_initializer())
b = tf.get_variable('bias', shape=[10], initializer=tf.zeros_initializer())

输入数据的shape=[None, 784]表示第一维接受任何长度的输入，第二维等于784是因为28x28=784。权重w使用均值为0,方差为1的正态分布，偏置b初始化为0。

然后定义预测结果、loss和优化函数

logits = tf.matmul(x, w) + b
entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(entropy, axis=0)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

使用tf.matmul做矩阵乘法，然后使用分类问题的loss函数交叉熵，最后将一个batch中的loss求均值，对其使用随机梯度下降法。

因为数据集中有测试集，所以可以在测试集上验证其准确率

preds = tf.nn.softmax(logits)
correct_preds = tf.equal(tf.argmax(preds, 1), tf.argmax(y, 1))
accuracy = tf.reduce_sum(tf.cast(correct_preds, tf.float32), axis=0)

首先对输出结果进行softmax得到概率分布，然后使用tf.argmax得到预测的label，使用tf.equal得到预测的label和实际的label相同的个数，这是一个长为batch的0-1向量，然后使用tf.reduce_sum得到正确的总数。

最后在session中运算，这个过程就不再赘述。

结果与可视化

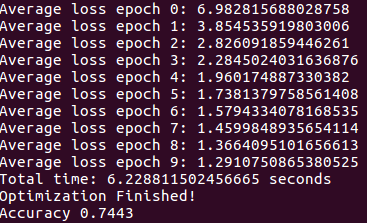
最后可以得到训练集的loss的验证集准确率如下

Paste_Image.png

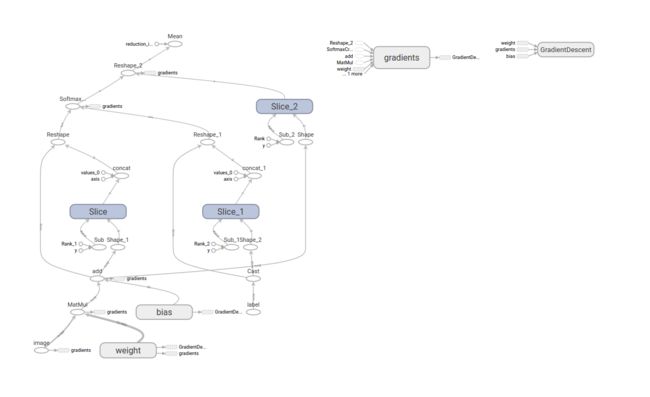
可以发现经过10 epochs，验证集能够实现74%的准确率。同时，我们还能够得到tensorboard可视化如下。

Paste_Image.png

这看着是有点混乱的，所以下一次课会讲一下如何结构化我们的模型。

---

本文的全部代码都在github

欢迎访问我的博客

欢迎查看我的知乎专栏，深度炼丹