支持向量机

一、什么是支持向量机

支持向量机(Suport Vector Machine,常简称为SVM），是一个监督式学习的方式。支持向量机属于一般化线性分类器，这类分类器的特点是能够同时最小化经验误差与最大化几何边缘区，因此支持向量机机也被称为最大边缘区分类器。

SVM.png

max margin.png

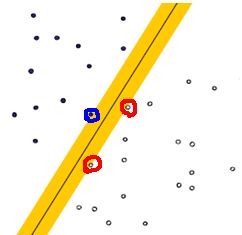
蓝色和红色的线圈出来的点就是所谓的支持向量，离分界线最近的点，如果去掉这些点，直线多半要改变位置。Classifier Boundary就是决策函数f(x)，在两个类的中间。红色和蓝色之间的间隙就是我们要的最大化分类的间隙。

二、关于拉格朗日乘子法和KKT条件

1.关于拉格朗日乘子法

有拉格朗日乘子法的地方，必然是一个组合优化问题。比如

这是一个带等式约束的优化问题，有目标值，有约束条件，不能直接求导。可以使用拉格朗日方法，把这个约束乘以一个系数加到目标函数中去，这样相当与既考虑了原目标函数，也考虑了约束条件。然后分别对x求导等于0，
$\begin{align} \frac{\partial{f}}{\partial{x_2}} = 4x_1+2\alpha_1 = 0 \implies x_1 = -0.5\alpha_1 \\ \frac{\partial f} {\partial x_2} = 6x_2+\alpha_1+2\alpha_2 = 0 \implies x_2 = -\frac{\alpha_1+2\alpha_2}{6} \\ \frac{\partial f}{\partial x_3} = 14x_3+3\alpha_2 = 0 \implies x_3 = -\frac{3\alpha_2}{14} \end{align}$
把它带点菜约束条件中去，可以看到，2个变量两个等式，最终可再带回去求x就可以了。更高一层，带有不等式的约束问题怎么办？需要用更一般化的拉格朗日乘子法，即KKT条件，来求解这个问题。

2.关于KKT条件

任何原始问题约束条件无非最多三种，等式约束，大于号约束，小于号约束，而这三种最终通过将约束方程简化成两类：约束方程等于0和约束方程小于0。

假设原始问题约束条件为下例所示：

那么把约束条件变个样子

现在拿到目标函数中去变成

那么KKT条件的定理是什么呢？就是如果一个优化问题在转变成

其中g是不等式约束，h是等式约束。那么KKT条件就是函数的最优值，它必定满足下面条件：

L对各个x求导为0

这三个等式很好理解，重点是第三个句子不好理解，因为我们知道在约束条件变完或，所有的，且求和还要为0。那么为什么KKT的条件是这样的呢？

某次的g(x)在为最优解起作用，那么它的系数值（可以）不为0，如果某次g(x)没有为下一次的最优解起作用，那么它的系数就必须为0。

三、函数间隔和几何间隔

函数间隔
对于给定的训练数据集T合超平面(w,b)，定义超平面(w,b)关于样本点的函数间隔为

函数间隔可以表示分类预测的正确性及确信度。但是选择超平面时，只有函数间隔是不够的，因子只要成比较改变和b，超平面并没有改变，但函数间隔却扩大了。

几何间隔
对于给定的训练数据集T和超平面，定义超平面关于样本点的几何间隔为,其中为的范数。

如果，那么函数间隔和几何间隔相等。如果超平面参数成比例地改变（超平面没有改变），函数间隔也成比例改变，而几何间隔不变。

四、间隔最大化

支持向量机的基本想法是求解能够正确分训练数据集并且几何间隔最大的分离超平面。对线性可分的训练数据集而言，线性可分分离超平面有无穷多个（等价于感知机），但是几何间隔最大的分离超平面时唯一的。这里的间隔最大化被称为硬间隔最大化。

间隔最大化的直观解释是：对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。也就是说，不仅将正负实例点分开，而且对最难分的实例点（离超平面最近的点）也有足够大的确信度将他们分开。这样的超平面应该对未知的新实例有很好的分类预测能力。

1.最大间隔分离超平面

下面考虑如何求一个几何间隔最大的分离超平面，即最大间隔分离超平面。具体地，这个问题可以表示为下面的约束最优化问题：

即我们希望最大化超平面关于训练数据集的集合间隔，约束条件表示的是超平面关于每个训练样本点的集合间隔至少是

考虑几何间隔和函数间隔的关系式，可将这个问题改成为

函数间隔并不影响最优化问题的解。事实上，假设将成比例改变为,这时函数间隔变成。函数间隔的改变对最优化问题的不等式约束没有影响，对目标函数的优化也没有影响，也就事实说，它产生一个等价的最优化问题。这样，就可以取。将代入上面的最优化问题。注意最大化和最小化是一样的。

于是就得到下面的线性可分支持向量机学习的最优化问题

这是一个凸二次规划问题(contex quadratic programming)问题。
凸优问题是指约束最优化问题

其中，目标函数和约束函数都是上的可连续可微的凸函数，约束函数是的仿射函数。当木匾函数是是二次函数且约束函数是仿射函数时，上述的凸优化问题成为凸二次规划问题。
如果求出约束最优化问题的解，那么就可以得出最大间隔分离超平面及决策函数，即线性可分支持向量机模型。

五、学习的对偶算法

为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用到拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解，这就是线性可支持向量机的对偶算法(dual algorithm)。这样做的优点，一是对偶问题往往根据容易求解；二是自然引入核函数，进而推广到非线性可分类问题。

首先构建拉格朗日函数(Lagrange function)。为此，对每一个不等式约束引入拉格朗日乘子(Lagrange multiplier)定义拉格朗日函数：

其中为拉格朗日乘子向量。

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题

为了得到对偶函数问题的解，需要先求对的极小，再求的极大
(1)求
将拉格朗日函数分别对求偏导数并令其等于0
$\begin{align} \bigtriangledown_{\omega}L(\omega,b,\alpha)=\omega-\sum_{i=1}^N\alpha_iy_ix_i=0 \\ \bigtriangledown_bL(\omega,b,\alpha) = -sum_{i=1}^N\alpha_iy_i=0 \\ \omega = \sum_{i=1}^N\alpha_iy_ix_i=0 \space(1)\\ \sum_{i=1}^N\alpha_iy_i=0 \space(2) \end{align}$

将（1）代入拉格朗日函数，并利用(2)，即可得
$\begin{equation}\label{eq1} \begin{split} L(\omega,b,\alpha)=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i*x_j)-\sum_{i=1}^N\alpha_iy_i((\sum_{j=1}^N\alpha_jy_jx_j)*x_i+b)+ \sum_{i=1}^N\alpha_i \\ =-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i*x_j)+\sum_{i=1}^N\alpha_i \end{split} \end{equation}$
即

(2)求对的极，即对偶问题

将公式(3)的目标函数由极大值转换成求极小，就得到下面与之等价的对偶最优化问题

(3)解
假设是对偶最优化问题的解，则存在下标使得，并求按下式求得原始最优化的解

根据KKT条件成立，即得
$\begin{equation}\label{eq1} \begin{split} \bigtriangledown_{\omega}L(\omega^*,b^*,\alpha^*) = \omega^*-\sum_{i=1}^N\alpha_i^*y_ix_i = 0\\ \bigtriangledown_b L(\omega^*,b^*,\alpha^*)=-\sum_{i=1}^N \alpha_i^*y_i =0 \\ \alpha_i^*(y_i(\omega^**x_i+b^*)-1) \ge 0,i=1,2,\dots,N \\ y_i(\omega^**x_i+b^*)-1 \ge 0,i =1,2,\dots,N \\ \alpha_i^* \ge 0 ,i =1,2,\dots,N \end{split} \end{equation}$
因此

,且至少存在一个，假设,那么不是原始问题的解,所以

那么分离的超平面可以写成

决策函数可以写成

由此可以看出，分类决策函数只依赖于输入x和训练样本输入的内积，式（8）称为线性可分支持向量机的对偶形式。

案例
训练数据正例点是，负例点是，试用线性可分支持向量机
解：根据所给数据，对偶问题是
$\begin{equation}\label{eq1} \begin{split} \mathop{\min}_{\alpha} \space \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i*x_j)-\sum_{i=1}^N\alpha_i \\ = \frac{1}{2}(18\alpha_1^2+25\alpha_2^2+2\alpha_3^2+42\alpha_1\alpha_2-12\alpha_1\alpha_3-14\alpha_2\alpha_3)-\alpha_1-\alpha_2-\alpha_3 \\ s.t. \space \alpha_1+\alpha_2-\alpha_3 = 0 \\ \alpha_i \ge 0,i =1,2,3 \end{split} \end{equation}$

两个向量和的点积定义为：

解这一优化问题，将代入目标函数并记为

对求偏导令其为0，易知处取极值，该点不满足约束条件，所以最小值应在边界上达到。

当，当，于是

这样,对应的实例点是支持向量，计算可得,

分离超平面为
分离决策函数为

六、软间隔最大化

线性可分问题的支持向量机学习方法，对线性不可分训练数据是不适用的，因为这时上述方法中的不等式约束不能都成立。线性不可分意味着不能满足函数间隔大于等于1的约束条件。为了解决这个问题，对每个样本点都引入一个松弛变量，使得函数间隔加上变量大于等于1，这样约束条件变为

同时对于每个松弛变量，支付一个代价,目标函数由原来的变成

C>0为惩罚参数，一般由应用问题解决，C值大时对误分类的惩罚增大，C值小时对误分类的惩罚减小。最小化木匾函数有2层意思：使得尽量小，即间隔尽量大，同时使误分类点的个数尽量小，C是调和两者的系数

七、非线性支持向量机与核函数

1.背景知识

(1)核技巧

非线性分类问题是指通过非线性模型才能很好地进行分类的问题。非线性问题往往不好求解，希望通过线性分类问题的方法解决这个问题，所采取的方法是进行一个非线性变换，将非线性问题变成线性问题，通过解变换后的线性问题的方法求解原来的非线性问题。

用线性分类方法求解非线性分类问题分两步：首先使用一个变换将原来空间的数据映射到新空间；然后在新空间里用线性分类学习方法从训练数据中学习分类模型。核技巧就属于这样的方法。

(2)核函数定义

设X是输入空间（欧氏空间的子集或离散集合），又设H为特征向量（希伯而空间H），如果存在一个从X到H的映射

使得对所有，函数满足条件

则称K(x,z)为核函数，为映射函数，。通常计算K(x,z)比较容易，而通话计算K(x,z)并不容易。

是输入空间到特征空间的迎神，特征空间一般是高维的，甚至是无穷维，可以看到，对于给定的核K(x,z)，特征空间H和映射函数的取法并不唯一，可以取不同的特征空间，即便是在同一特征空间也可以取不同的映射。

(3)核技巧在支持向量机中的应用

在对偶目标函数中的内积可以用核函数来代替，此时对偶问题的目标函数成为

这等价于经过映射函数将原来的输入空间变换到一个新的特征空间，将输入空间中的内积变换成特征空间中的内积，在新的特征空间里从训练样本中学习线性支持向量机。学习是隐式地在特征空间进行的，不需要显式地定义特征空间和营业日函数。在实际应用中，往往依赖领域知识直接选择核函数。

2.常用核函数

(1)多项式核函数(polynomial kernal function)

对应的支持向量机是一个p次多项式分类器，在此情形下，分类决策函数成为

(2)高斯核函数(Guassian kernel function)

对应的支持向量机是高斯径向基函数(radial basis function)分类器。在此情形下，分类决策函数成为

(3)字符串核函数

核函数不仅可以定义在欧式空间，还可以定义在离散数据的集合上。比如，字符串核函数是定义在字符串集合上的核函数。字符串核函数在文本分类、信息检索、生物信息学等方面都有应用。

两个字符串s和t上的字符串核函数是基于映射的特征空间中的内积：

字符串核函数给出了字符串s和t中长度等于n的所有子串组成的特征向量的余弦相似度。直观上看，两个字符串相同的字串越多，它们就越相似，字符串核函数的值就越大。字符串核函数可以由动态规划快速地计算。

八、序列最小最优化算法

支持向量机的学习问题可以形式化为求解凸二次规划问题，这样的凸二次规划问题具有全局最优解，并且有许多最优化算法可以用于这一问题的求解。但是当训练样本容量很大时，这些算法往往变得非常低效，以至无法使用。

序列最小最优化(sequential minimal optimization,SMO)算法，是一种启发式算法，其基本思路是：如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。否则，选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题的目标是使函数值变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。子问题有两个变量，一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。

1.两个变量二次规划的求解办法

假设两个变量是，其他变量是固定的，于是SNO的最优化问题的子问题可以写成。

$\begin{align} \mathop{min}_{\alpha_1,\alpha_2} \space W(\alpha_1,\alpha_2)=\frac{1}{2}K_{11}\alpha_1^2+\frac{1}{2}K_{22}\alpha_2^2+y_1y_2K_{12}\alpha_1\alpha_2 \\ -(\alpha_1+\alpha_2)+y_1\alpha_1\sum{i=3}^Ny_i\alpha_iK_{i1}+y_2\alpha_iK_{i2} \space(7.1) \\ s.t. \alpha_1y_1+\alpha_2y_2 = - \sum_{i=3}^N y_i \alpha_i = \zeta \space(7.2)\\ 0 \leq \alpha_i \leq C \space(7.3) (i =1,2) \end{align}$
其中，是常数，目标函数中省略不含的常数项。

为了求解两个变量的二次规划问题，约束可以用二维空间中的图形表示

二变量优化问题.png

不等式约束(7.3)使得在盒子[0,C][0,C]内，等式约束(7.2)使在平行于盒子[0,C][0,C]的对角线的直线上。因此要求的是目标函数在一条平行于对角线的线段上最优值。这使得两个变量的最优化问题成为实质上的单变量最优化文图，不访考虑为变量的最优化问题。

假设初始化可行解为，最优化解为，并且假设沿着约束方向未经剪辑时的最优解为

由于需满足不等式约束(7.3)，所以最优值的取值范围必须满足条件

其中，L与H是所在对角线段端点的界，如果

如果，则

下面首先要求沿着约束方向未经剪辑即未考虑不等式约束(7.3)时的最优解，然后在解决剪辑后的解，我们用定理来描述这个结果

令

当i=1,2时，为函数g(x)对输入的预测值与真实输出之差

定理最优化问题(7.1)~(7.3)沿着约束方向未经剪辑时的解是

其中
是输入空间到特征空间的映射

经剪辑后的的解是

由是