CDUT新生摸底训练1 解题报告

CDUT新生摸底训练1 解题报告

除了I题皆水题

---

A.A + B Problem

Calculate A + B.

Input

Each line will contain two integers A and B. Process to end of file.

Output

For each case, output A + B in one line.

Sample Input

1 1

Sample Output

2

除了格式可能会出错,我想不出其它写不出来的原因。

#include 
#include 
using namespace std;
int main()
{
    long long a,b;
    while(scanf("%lld %lld",&a,&b)!=EOF)
    {
        printf("%lld\n",a+b);
    }
    return 0;
}

---

B.杨辉三角

还记得中学时候学过的杨辉三角吗？具体的定义这里不再描述，你可以参考以下的图形：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

Input

输入数据包含多个测试实例，每个测试实例的输入只包含一个正整数n（1<=n<=30），表示将要输出的杨辉三角的层数。

Output

对应于每一个输入，请输出相应层数的杨辉三角，每一层的整数之间用一个空格隔开，每一个杨辉三角后面加一个空行。

Sample Input

2 3

Sample Output

1
1 1

1
1 1
1 2 1

递推啊,f(i,j)为i行j列的数字,f(i,j)=f(i-1,j-1)+f(i-1,j),没了。

格式很坑。。。

#include 
#include 
#include 
using namespace std;
int m[31][31];
int main()
{
    memset(m,0,sizeof(m));
    int n;
    m[1][1]=1;
    m[2][1]=m[2][2]=1;
    int maxn=2;
    while(scanf("%d",&n)!=EOF)
    {
        if(n>maxn)
        {
            for(int i=maxn;i<=n;i++)
            {
                for(int j=1;j<=i;j++)
                {
                    m[i][j]=m[i-1][j-1]+m[i-1][j];
                }
            }
            maxn=n;
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j

---

C.六教的楼梯

Problem Description

有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？

Input

输入数据首先包含一个整数N，表示测试实例的个数，然后是N行数据，每行包含一个整数M（1<=M<=40）,表示楼梯的级数。

Output

对于每个测试实例，请输出不同走法的数量

Sample Input

2
2
3

Sample Output

1
2

递归模板题,话是这么说,但我刚开始tle了。。。

先处理完，再输出(询问有点多,但数据很小)

#include 
#include 
#include 
#include 
#include 
using namespace std;
int cnt=0;
const int maxn=40;
int ans[41];
bool cald[41];
void done(int fl)
{
    ans[fl]++;
    if(fl+1<=maxn)
    {
        done(fl+1);
    }
    if(fl+2<=maxn)
    {
        done(fl+2);
    }
    return ;
}
int main()
{
    int n,m;
    scanf("%d",&n);
    done(1);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&m);
        cout<

---

D.最大字母

对于输入的每个字符串，查找其中的最大字母，在该字母后面插入字符串“(max)”。

Input

输入数据包括多个测试实例，每个实例由一行长度不超过100的字符串组成，字符串仅由大小写字母构成。

Output

对于每个测试实例输出一行字符串，输出的结果是插入字符串“(max)”后的结果，如果存在多个最大的字母，就在每一个最大字母后面都插入"(max)"。

Sample Input

abcdefgfedcba
xxxxx

Sample Output

abcdefg(max)fedcba
x(max)x(max)x(max)x(max)x(max)

扫一次,记录最大,输出时比较再在后面加(max)就完了。

但很迷，我用字符串过不了，用字符数组就过了

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
char str[105];
int main()
{
    while(gets(str))
    {
        char maxn='A';
        int n=strlen(str);
        for(int i=0;i

---

E.Boss GoghV

You are both a shop keeper and a shop assistant at a small nearby shop. You have goods, the i

coins.

You got tired of remembering the price of each product when customers ask for it, thus you decided to simplify your life. More precisely you decided to set the same price for all n

goods you have.

However, you don't want to lose any money so you want to choose the price in such a way that the sum of new prices is not less than the sum of the initial prices. It means that if you sell all n

goods for the new price, you will receive at least the same (or greater) amount of money as if you sell them for their initial prices.

On the other hand, you don't want to lose customers because of big prices so among all prices you can choose you need to choose the minimum one.

So you need to find the minimum possible equal price of all n

goods so if you sell them for this price, you will receive at least the same (or greater) amount of money as if you sell them for their initial prices.

You have to answer q

independent queries.

Input

The first line of the input contains one integer q

() — the number of queries. Then q

The first line of the query contains one integer n

( — the number of goods. The second line of the query contains n (1≤*a**i≤107 is the price of the i*

Output

For each query, print the answer for it — the minimum possible equal price of all n

goods so if you sell them for this price, you will receive at least the same (or greater) amount of money as if you sell them for their initial prices.

Example

Input

3
5
1 2 3 4 5
3
1 2 2
4
1 1 1 1

Output

3
2
1

实际上是CF590的A题，加起来除n，小于原总价就++

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    int num;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&num);
        int tmp;
        int sum=0;
        for(int j=1;j<=num;j++)
        {
            scanf("%d",&tmp);
            sum+=tmp;
        }
        int ans=sum/num;
        if(ans*num

---

F.社交网络

你正在一个流行的社交网络中通过智能手机发送信息。你的智能手机最多可以显示k个最近与朋友的对话。最初，屏幕是空的（即显示的对话数等于0）。 每次谈话都是你和你的一些朋友之间的。最多只能和你的朋友进行一次谈话。所以每次谈话都是由你的朋友来定义的。

​ 现在你（突然！）有能力看到未来。你知道在一天中你将收到n条信息，第i条信息将从id为idi（1≤idi≤10^9）的朋友处收到。 如果在智能手机当前显示的对话中收到来自IDI的消息，则不会发生任何事情：屏幕上的对话不会更改，也不会更改其顺序，您将阅读该消息并继续等待新消息。 否则（即，如果屏幕上没有与IDI的对话）：

首先，如果屏幕上显示的对话数为k，则从屏幕上删除最后一个对话（位置为k）。 现在，屏幕上的对话数保证小于k，并且与朋友idi的对话不会显示在屏幕上。 与朋友idi的对话出现在屏幕的第一个（最上面的）位置，所有其他显示的对话都向下移动一个位置。

你的任务是在处理完所有n条消息后查找对话列表（按对话在屏幕上显示的顺序）

Input

输入的第一行包含两个整数n和k（1≤n，k≤200）-您的智能手机可以显示的消息数和对话数。 输入的第二行包含n个整数id1，id2，…，idn（1≤id i≤10^9），其中idi是向您发送第i条消息的朋友的id。

Output

在输出的第一行中，打印一个整数m（1≤m≤m in（n，k））——接收所有n条消息后显示的会话数。 在第二行中，打印m个整数ids1、ids2、…、idsm，其中idsi应等于收到所有n条消息后显示在位置i上的对话对应的朋友的id。

Examples

​ Input

7 2
1 2 3 2 1 3 2

​ Output

2
2 1 

​ Input

10 4
2 3 3 1 1 2 1 2 3 3

​ Output

3
1 3 2 

CF590的B题

模拟，没了！

#include 
#include 
#include 
#include 
#include 
using namespace std;
int que[201];
int main()
{
    int n,k;
    int cnt=0;
    int st=1;
    int ed=0;
    scanf("%d %d",&n,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&que[++ed]);
        cnt++;
        for(int j=st;jk)
        {
            st++;
            cnt--;
        }
    }
    cout<=st;i--)
    {
        cout<

---

G.新生见面会

Problem Description

Do you know what is called Coprime Sequence''? That is a sequence consists of *n* positive integers, and the GCD (Greatest Common Divisor) of them is equal to 1.Coprime Sequence'' is easy to find because of its restriction. But we can try to maximize the GCD of these integers by removing exactly one integer. Now given a sequence, please maximize the GCD of its elements.

Input

The first line of the input contains an integer T(1≤T≤10), denoting the number of test cases.
In each test case, there is an integer n(3≤n≤100000) in the first line, denoting the number of integers in the sequence.
Then the following line consists of n integers a1,a2,...,an(1≤ai≤109), denoting the elements in the sequence.

Output

For each test case, print a single line containing a single integer, denoting the maximum GCD.

Sample Input

3
3
1 1 1
5
2 2 2 3 2
4
1 2 4 8

Sample Output

1
2
2

如果每次试一次删去后的最大复杂度肯定是无法接受的(废话)，我们可以从前往后扫，记录前i个的最大gcd，同理，从后往前扫，记录后i个的最大gcd,再扫一次枚举删去i比较前i-1的最大gcd和后i+1的最大gcd。

#include 
#include 
#include 
#include 
#include 
using namespace std;
int fr[100005];
int ba[100005];
int num[100005];
int gcd(int a,int b)
{
    int tmp;
    while(b>0)
    {
         tmp=a%b;
         a=b;
         b=tmp;
    }
    return a;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&num[i]);
        }
        fr[1]=num[1];
        ba[n]=num[n];
        for(int i=2;i<=n;i++)
        {
            fr[i]=gcd(fr[i-1],num[i]);
        }
        for(int i=n-1;i>=1;i--)
        {
            ba[i]=gcd(ba[i+1],num[i]);
        }
        int maxn=0;
        maxn=max(maxn,fr[n-1]);
        maxn=max(maxn,ba[2]);
        for(int i=2;i<=n-1;i++)
        {
            int tmp=gcd(fr[i-1],ba[i+1]);
            maxn=max(maxn,tmp);
        }
        cout<

---

H.GoghV的木棍

Problem Description

Given a set of sticks of various lengths, is it possible to join them end-to-end to form a square?

Input

The first line of input contains N, the number of test cases. Each test case begins with an integer 4 <= M <= 20, the number of sticks. M integers follow; each gives the length of a stick - an integer between 1 and 10,000.

Output

For each case, output a line containing "yes" if is is possible to form a square; otherwise output "no".

Sample Input

3
4 1 1 1 1
5 10 20 30 40 50
8 1 7 2 6 4 4 3 5

Sample Output

yes
no
yes

dfs搜就完事了，先把所有长度加起来/4就是正方形的边长，再从第1边开始尝试是否能组成一条边。
再来剪枝，首先可以想到如果找到可行的答案就可以结束了(但是只有这个不够，开始我就tle了)，再来，如果一根木棍在枚举顺序前面却没有用那么还要考虑它吗?答案显然是否定的，dfs尝试下一个的时候就把当前的枚举位传过去，下次枚举就从上次枚举的地方开始。

#include 
#include 
#include 
#include 
#include 
using namespace std;
int stk[21];
bool used[21];
bool flag=0;
int sum;
int m;
void dfs(int id,int left,int dx)
{
    if(flag)
    {
        return ;
    }
    if(id==3 && left==0)
    {
        int nsum=0;
        for(int i=1;i<=m;i++)
        {
            if(!used[i])
            {
                nsum+=stk[i];
            }
        }
        if(nsum==sum/4)
        {
            flag=1;
            return ;
        }
    }
    if(left==0)
    {
        dfs(id+1,sum/4,1);
    }
    for(int i=dx;i<=m;i++)
    {
        if(!used[i])
        {
            if(stk[i]<=left)
            {
                used[i]=1;
                dfs(id,left-stk[i],i+1);
                used[i]=0;
            }
        }
    }
    return ;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        memset(used,0,sizeof(used));
        flag=0;
        sum=0;
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            scanf("%d",&stk[i]);
            sum+=stk[i];
        }
        if(sum%4)
        {
            cout<<"no"<

---

I.mool的多边形

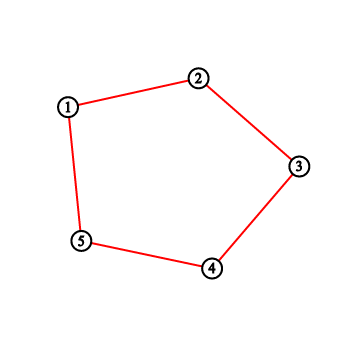
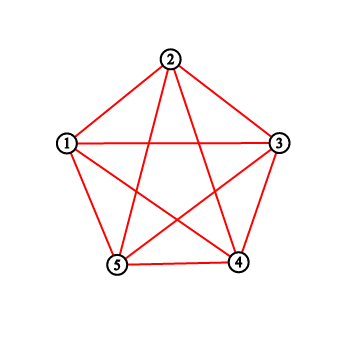
PolandBall has such a convex polygon with n veritces that no three of its diagonals intersect at the same point. PolandBall decided to improve it and draw some red segments.

He chose a number k such that gcd(n, k) = 1. Vertices of the polygon are numbered from 1 to n in a clockwise way. PolandBall repeats the following process n times, starting from the vertex 1:

Assume you've ended last operation in vertex x (consider x = 1 if it is the first operation). Draw a new segment from vertex x to k-th next vertex in clockwise direction. This is a vertex x + k or x + k - n depending on which of these is a valid index of polygon's vertex.

Your task is to calculate number of polygon's sections after each drawing. A section is a clear area inside the polygon bounded with drawn diagonals or the polygon's sides.
Input

There are only two numbers in the input: n and k (5 ≤ n ≤ 106, 2 ≤ k ≤ n - 2, gcd(n, k) = 1).
Output

You should print n values separated by spaces. The i-th value should represent number of polygon's sections after drawing first i lines.
Examples
Input
Copy

5 2

Output
Copy

2 3 5 8 11

Input
Copy

10 3

Output
Copy

2 3 4 6 9 12 16 21 26 31

Note

The greatest common divisor (gcd) of two integers a and b is the largest positive integer that divides both a and b without a remainder.

For the first sample testcase, you should output "2 3 5 8 11". Pictures below correspond to situations after drawing lines.

本场最难题，先找规律，观察可得，样例的前两次加边每次都只能多一块区域，而到了第三，四次的加边却加了两块区域，为什么呢？因为区域增加的本质是加的线段和其它线段发生了交叉，使线段被分割而产生了更多区域。

可以得到一个推论每次加边产生的区域数等于新产生交点的数+1。

那么如何判断两条边是否相交呢？可以发现一个线段和另一个线段的相交取决于它们端点的情况。如果一个线段的端点在另一个线段的两端点内，那么两线段就相交。

如何判断呢？首先可以想到用数组在相应的位置+1，每次统计那个区间加起来有多少就行了。但这样的话时间复杂度就有n^2了，无法接受。虽然据说有其它解决办法，但本蒟蒻不会QAQ，可以想到用线段树(为什么是线段树呢？因为我不会写树状数组了。。。)来维护区间信息达到nlogn的复杂度。

#include 
#include 
#include 
#include 
#include 
using namespace std;
long long tree[1000005<<2];
long long num[1000005];
void build(int root,int l,int r)
{
    if(l==r)
    {
        tree[root]=num[l];
        return ;
    }
    int mid=(l+r)>>1;
    build(root<<1,l,mid);
    build(root<<1|1,mid+1,r);
    tree[root]=tree[root<<1]+tree[root<<1|1];
    return ;
}
void updata(int root,int l,int r,int pos,int val)
{
    if(rpos)
    {
        return ;
    }
    if(l==r)
    {
        if(l==pos)
        {
            tree[root]+=val;
        }
        return ;
    }
    int mid=(l+r)>>1;
    if(pos<=mid)
    {
        updata(root<<1,l,mid,pos,val);
    }
    else
    {
        updata(root<<1|1,mid+1,r,pos,val);
    }
    tree[root]=tree[root<<1]+tree[root<<1|1];
}
long long query(int root,int l,int r,int ql,int qr)
{
    if(ql>r||qr=r)
    {
        return tree[root];
    }
    int mid=(l+r)>>1;
    long long ans=0;
    ans+=query(root<<1,l,mid,ql,qr);
    ans+=query(root<<1|1,mid+1,r,ql,qr);
    return ans;
}
int main()
{
    long long n,k;
    cin>>n>>k;
    long long ans=1;
    if(2*k>n)
    {
        k=n-k;
    }
    build(1,1,n);
    int now=1;
    for(int i=1;i<=n;i++)
    {
        int next=now+k;
        ans+=1;
        if(next>n)
        {
            ans+=query(1,1,n,now+1,n)+query(1,1,n,1,next-n-1);
        }
        else
        {
            ans+=query(1,1,n,now+1,next-1);
        }
        cout<n)
        {
            next-=n;
        }
        updata(1,1,n,next,1);
        now=next;
    }
    return 0;
}

---

J.sudoku的AB串

Nikolay got a string of length nab to n

He wants to modify his string so that every its prefix of even length has an equal amount of letters 'a' and 'b'. To achieve that, Nikolay can perform the following operation arbitrary number of times (possibly, zero): choose some position in his string and replace the letter on this position with the other letter (i.e. replace 'a' with 'b' or replace 'b' with 'a'). Nikolay can use no letters except 'a' and 'b'.

The prefix of string s

of length (1≤l≤n

.

For example, for the string s=

"abba" there are two prefixes of the even length. The first is "ab" and the second s[1…4]=

Your task is to calculate the minimum number of operations Nikolay has to perform with the string s

to modify it so that every its prefix of even length has an equal amount of letters 'a' and 'b'.

Input

The first line of the input contains one even integer n

(2≤n≤2⋅105)

.

The second line of the input contains the string s

of length

, which consists only of lowercase Latin letters 'a' and 'b'.

Output

In the first line print the minimum number of operations Nikolay has to perform with the string s

to modify it so that every its prefix of even length has an equal amount of letters 'a' and 'b'.

In the second line print the string Nikolay obtains after applying all the operations. If there are multiple answers, you can print any of them.

Examples

Input

Copy

4
bbbb

Output

Copy

2
abba

Input

Copy

6
ababab

Output

Copy

0
ababab

Input

Copy

2
aa

Output

Copy

1
ba

Note

In the first example Nikolay has to perform two operations. For example, he can replace the first 'b' with 'a' and the last 'b' with 'a'.

In the second example Nikolay doesn't need to do anything because each prefix of an even length of the initial string already contains an equal amount of letters 'a' and 'b'.

刚开始题面的数据范围写错了，结果我写字符数组wa了n次。。。
很好想，每两个两个的检查，将多的那个字母改掉。

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    int n;
    cin>>n;
    string str;
    cin>>str;
    int na=0,nb=0;
    int ans=0;
    for(int i=0;i

---

虽然是水题赛(除了I题)，但还是吃了不少罚时QAQ。还是要提高编码准确性啊