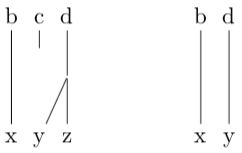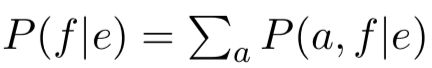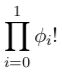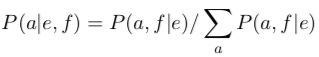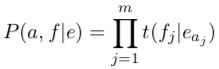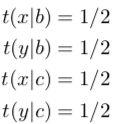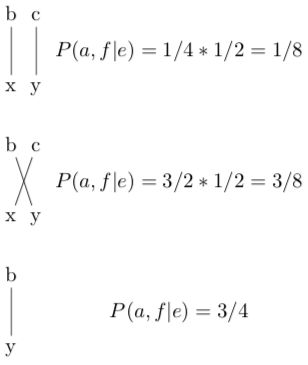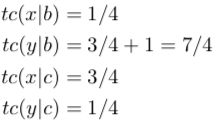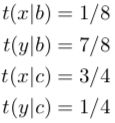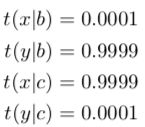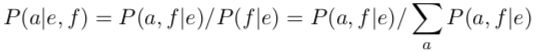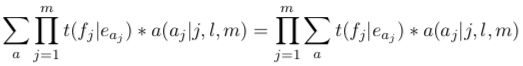译文：统计机器翻译教程—

原文 A Statistical MT Tutorial Workbook 由 Kevin Knight 于1999年完成。
原文及原作者链接：https://kevincrawfordknight.github.io/

本译文已获得原作者 Kevin Knight 的许可
我相信阅读英语原文是学习此内容的最佳方式

不知道这是什么？阅读本译文的前言

十九、词对齐（Word-for-Word Alignments）

（译者注：中文里往往我们把单个汉字称为“字”，多个汉字组成的词语称为“词”，但在本文的语境下，除非明确说明，所有的“字”，“词”，均指一个“单词”）

现在，我们需要思考两个东西。首先，我们如何自动地从语料库数据中获得参数值？第二，有了参数值后，给定任意句子组（译者注：一组句子由一个英语句子和一个法语句子组成），我们如何计算它们的 P(f|e)？

首先，思考一下如何自动从语料库数据中获得参数 n，t，p 和 d 的值。如果我们有一大堆英语句子和一大堆基于它们重写出来的法语句子，那一切都会很容易。要计算 n(0|did)，我们只需要找出每一个 “did” ，然后看看在重写的第一步中它发生了什么。如果 “did”出现了 15000 次，在重写第一步中被删除了 13000 次，那么 n(0|did) = 13/15。

练习题：准备 10000 条英语句子，把他们重写成法语句子，重写过程中的所有句子也保存起来。不，准备一百万条句子！哈哈，开玩笑的。别做这道练习题。

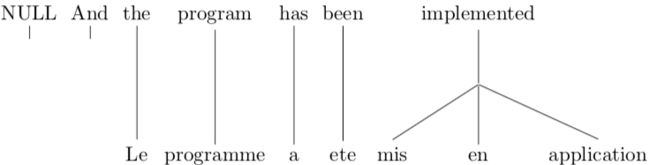
拥有一个既简单，同时又保留了这个模型所作出的绝大多数决定的数据结构，对我们来说，是非常有用的。这样的数据结构被称为词对齐。看一个例子：

注意看 NULL：它是不可见的，位于位置 0 作为句子的起点

如果我们有大量的这样被对齐的句子组，重复一遍，那一切都会很容易。要计算 n(0|did)，只需要看 “did” 和“没有法语单词”连接了多少次。要计算 t(maison|house)，只需要看所有的 “house” 生成的所有的法语单词，以及这些单词中是 “maison” 的次数。

与 Model 3 最契合的词对齐，是每一个法语单词都刚好只连接一个英语单词（不管正常单词还是 NULL）。所以，两个英语单词一起生成某个法语单词的情况永远都不会出现。这很糟糕，因为有时这样的对齐方式是不够客观的。

计算机是不擅长画画的，所以我们用由整数组成的向量（a vector of integers）来表示对齐会更方便。此向量的长度和法语句子的长度一致，向量中的每个元素对应一个法语单词。每个元素存储的值是这个法语单词在对齐图中所连接的英语单词的位置。我们可以这样表示上面的对齐例子：[2, 3, 4, 5, 6, 6, 6]。

练习题：对于句子 “Mary did not slap the green witch” 和 “Mary no daba una botefada a la bruja verde”，把它们的词对齐情况画出来。

练习题：如何用向量来表示上一题的词对齐？

注意，词对齐并没有保留模型在把英语句子翻译成法语时所做出的所有决定。比如，如果一个英语单词 x 和法语单词 y 和 z 相连接，那么我们其实不需要知道它们是否是按顺序生成的，或者它们是否被生成为 y 和 z 然后被进行了重新排序。后面当我们搞清楚如何计算 P(f|e) 时，这个问题其实是造成了一些后果的。

二十、根据词对齐来估算参数值

上一节中我们提到如何从词对齐的句子组中估算 n 和 t 参数。估算 d 参数也是很容易的。在对齐中，每一个连接都会为某特定参数比如 d(5|2,4,6) 增加次数。一旦我们拿到所有的次数，就可以得到最终的概率参数值。比如，如果当句子的长度分别是 4 和 6 时，我们观察到位于位置 2的英语单词生成了125次位于位置 5 的法语单词，那次数 dc(5|2,4,6) 就是 125。如果“总数”是所有 j 的 dc(j|2,4,6) 的和，那么 d(5|2,4,6) = dc(5|2,4,6)/总数。用第三节描述的求和符号：

最后要估算的就是 p₁ 的值了。我们可以认为整个法语句子库的单词数量为N。通过查看对齐结果，可以知道其中的 M 个单词是被 NULL 生成的。（其他的 N - M 个单词是被正常单词生成的。）然后我们可以想象，每一个被正常生成的法语单词后，在一共 N-M 的情况中，有 M 种情况，会有一个“伪造”单词被生成，因此，p₁ = M/(N-M)。

练习题：根据下面的对齐，估算出 n，t，p 和 d 的参数值：

二十一、拔靴法（Bootstrapping）

要估算出一个比较好的参数，我们需要一个非常庞大的已经翻译好了的语料库。这样的语料库确实存在，但通常没有进行词对齐。但我们可以从这些没有被对齐的句子中估算出参数，像魔法一样。当时我理解到这个概念的时候非常开心，同时我也可以把这个概念运用到其他问题中。

练习题：为了让你有一个直观的感受，尝试手动将 Kevin Knight 于 1997 年通过杂志 AI Magazine 发表的文章 Automating Knowledge Acquisition for Machine Translation 里的 84 组句子进行词对齐。

一个稍微更正式一点的直观感受是，对于翻译语料库里的一组英语和法语句子，两个对应位置的单词可能确实是互译的，但也可能不是。但如果我们更粗暴地看待哪个法语单词对应哪个英语单词，那关于它们的失真概率的信息就可以开始收集了。我们可能注意到，英语句子里的第一个单词和法语句子里的第一个单词通常都是互译的，那就可以假设 d(1|1,l,m) 的值是非常高的。此外，如果法语句子比英语句子长很多，我们可以猜测英语句子里的部分单词可能有很高的繁衍值，只不过我们不清楚具体是哪些单词而已。

这个概念就是，我们可以逐渐收集信息，每一条新的信息都会帮助我们去收集下一条信息。这被称为拔靴法。

二十二、所有可能的对齐方式

对于拔靴法来说，对齐是关键的部分。如果每一组句子，都有一个正确的对齐方式，那么我们可以用这些正确的对齐方式直接估算出参数。现在做这样的假设，对于每一组句子，我们无法决定哪一个对齐方式是正确的。假设一组句子里有 2 个看起来都很不错的对齐方式，那对于这样的一组句子，我们决定同时从这 2 个对齐方式中获得参数。但因为我们始终不确定哪一个对齐方式是正确的，相比较那些我们比较确定的句子组，从这样的句子组里拿到的参数，我们可能想打一些“折扣”。比如，从 2 个对齐方式中拿到的次数我们都乘以 0.5。如果单词 “house” 和单词 “maison” 只在其中一个对齐方式里是相连接的，那我们可以认为 “house” 和 “maison” 连接了 0.5 次。这可能没什么意义——你可以看到一个事件发生了 1 次， 2次，3 次，但你怎么可能看到它发生 0.5 次？先不要怀疑它！我们称这为分值计数（fractional counts）。

在实际问题里，我们不可能把事件简化到只有一两个可能的对齐方式。一定程度上，对于一组句子，所有的对齐方式都是有可能的。

练习题：一组包含 l 个英语单词和 m 个法语单词的句子里，有多少种可能的对齐方式？（别忘了 NULL）。

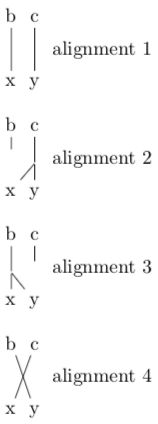
练习题：对于只有两个单词 “b c” 的英语句子和只有两个单词 “x y” 的法语句子，有多少种对齐的方式？我把其中一些方式画出来了，请你把其他的补充完整。

练习题：假设 b = blue，c = house， x = maison，y = bleue。在上面的对齐方式里，把你觉得正确的圈出来。

二十三、收集分值计数

如果对于一组句子，有两个可能的对齐方式，那我们可以认为它们都很不错。另一方面，我们可能也有理由相信，其中一个是更好的。这样的话，我们可以分别给这两个对齐 0.2 和 0.8 的权重。这些权重会用来计算分值计数。由于第二个对齐的权重更高，它“有更多的资本去挥霍”，因此，对最终的 n，t，p 和 d 参数，它的影响会更大。

现在我们把权重加到刚刚的对齐中去：

练习题：用分值计数来估算单词翻译的概率值 t(y|b)。

我们可以对一个有很多组句子的语料库做同样的事情。把所有句子组的对齐方式的分值计数收集起来，给它们权重，然后就可以估算出 n，t，p 和 d 参数。我知道你在想：我们从哪获取权重值？

二十四、对齐概率

现在用对齐概率来替代对齐权重吧。就是说，对于一组句子，我们提问：单词们被这样对齐和被那样对齐的概率都是多少？用上一节例子中的方式，一组句子的所有可能的对齐方式的概率值加起来应该等于 1。

这样的概率，我们写成 P(a|e, f)（译者注：e 和 f 分别是给定的英语句子和法语句子，顺序是 P(a|(e, f)) 而不是 P((a|e),f)。）。记住，对齐方式 a 只不过是一组整数组成的向量，它代表了不同法语单词所连接的英语单词的位置。

一个对齐方式是怎样比另一种的概率高的？嗯...，如果有人神奇地把单词翻译参数 t 的值给我们，那我们可以用 t 来判断对齐概率。在一个对齐方式里，相互连接的英语和法语单词的翻译概率越高，那这个对齐方式的对齐概率越高。反过来，翻译概率越低，对齐概率就越低。

我现在要做一个很棒的转换：

练习题：证明它。提示：

所以，要计算 P(a|e, f)，我们需要计算以下两个值的比。第一个是 P(a, f|e)，幸运的是，我们可以用 Model 3 的生成理论来计算它。对于一个英语句子 e，Model 3 带我们做了很多的决定（繁衍值，单词翻译，排序等等）。这些决定决定了对齐方式和最终的法语句子。记住对齐方式本身不过是一组连接位置的东西。（同样的对齐方式可以产生两句完全不同的法语句子）

第二值是 P(f|e)，回到第十九节的开头部分，我们说过我们想做两件事情。第一是从语料库中获得翻译模型的参数值，第二是通过参数值计算 P(f|e)。后者是我们的最终目标——把法语翻译回英语，即 P(e) * P(f|e) 的最大值就是最有可能的翻译。

我们快要“一石二鸟”了。一个英语句子 e，有很多种办法可以把它翻译成同一个法语句子 f。每一种办法对应了一种对齐方式。（多种对齐方式可以生成同一个法语句子）

因此：

所以，我们把这两个问题变成了一个问题，计算公式 P(a,f|e)。

二十五、P(a,f|e)

Model 3 的生成理论完全没有讨论关于对齐的事情。但对齐却是一种可以将生成理论所作出的不同决定进行整理总结的方式。生成某个特定的对齐方式和法语句子的概率基本上就是一些更小的概率之积，比如给某个单词提供繁衍值 n，提供翻译概率 t，把一个单词从英语句子中的位置 i 移动到法语句子中的位于位置 j(d) 等等。

我们先来整理一下。

e = 英语句子
f = 法语句子
e_i = 第 i 个英语单词
f_j = 第 j 个英语单词
l = 英语句子的单词个数
m = 法语句子的单词个数
a = 对齐方式 (由整数 a₁,...,a_m 组成的向量，元素 a_j 的值的范围是 0 到 1 的闭区间）
a_j = 在对齐方式 a 中的第 j 个法语单词所连接的英语单词的位置
e_a_j = 在对齐方式 a 中的第 j 个法语单词所连接的真正的英语单词（译者注：e_a_j 是一个错误的写法，原文的正确写法是 a 作为 e 的下标，然后 j 作为 a 的下标，但我没找到写下下标的方式）
φ_i = 在对齐方式 a 里，英语单词 i 的繁衍值（值的范围是 0 到 1的闭区间）

这个公式考虑到了对齐方式和法语句子所暗示出来的基本繁衍值，单词翻译，失真值。但还有一些问题。

第一个问题是我们只应该考虑由真正的英语单词生成的法语单词的失真值，而不是由 NULL 生成的。我们应该排除所有 a_j = 0 的 d 值。

一个相关的问题是我们忘了生成“伪造的”法语单词是有代价的。任何 a_j = 0 的法语单词都是“伪造的”。根据上面的定义，“伪造”单词有 φ₀ 个。注意这里有 m - φ₀ 个正常单词，即被真正的英语单词生成的法语单词。对于每一个正常单词的后面，我们基于概率 P₁ 选择性地插入一个“伪造”单词。这个过程里，有多少种方式可以把 φ₀ 个 “伪造”单词插进去？这个问题和从 m - φ₀ 个球里拿出 φ₀ 个球有多少种方式是一样的。

比如，有一个办法可以生成刚好 0 个“伪造”单词——总是选择不插入。事实上有 m - 1 种方法可以生成刚好 1 个“伪造”单词。你可以在第一个真正的单词后插入一个伪造单词，也可以在第二个真正的单词之后，等等，或者也可以在第 m 个真正的单词后插入。所以 P(a, f|e) 有另一个因子了：

别忘了插入“伪造”单词是有代价的。如果我们插入 φ₀ 个 “伪造”单词，那我们还要考虑一个因子 p₁^φ₀，如果我们没有插入 ((m − φ₀) − φ₀) 个“伪造”单词，那我们又要考虑一个因子 p₀^(m-φ₀)。

练习题：为什么我会写成 ((m − φ₀) − φ₀) 而不是写成 (m − φ₀)?

第三个问题是，我们忘了把“伪造”单词插到最终的位置里也是有代价的。回想一下第十七节，我们并没有像 d(j|0,l,m) 这样的失真概率公式。相反，我们在生成法语句子的最后一步里，把“伪造”单词插入剩下的空位。由于这样可能性一样的排序方式有 φ₀! 种，那么为了计算 P(a|, f|e)，最终生成的任何顺序都需要加一个额外的因子 1/ (φ₀!)。

由于词对齐把 e 转换成 f 的生成过程中的一小部分信息给丢失了，回想下第十九节中的 “... 如果一个英语单词 x 和法语单词 y 和 z 相连接，那么我们其实不需要知道它们是否是按顺序生成的，或者它们是否被生成为 y 和 z 然后被进行了重新排序...”，一个简单地把 x 连接到 y 和 z 的词对齐将这个信息丢掉了。这就像，我掷两次骰子，然后我说结果是 4-3，但不说哪个骰子的结果是 4，哪个骰子的结果是 3，那么就会有两种掷出 4-3 的方式。如果是掷三次呢？掷出 6-4-1 的方式有多少种？有六种方式：如果第一个骰子的结果是 6，就有俩种方式，如果第一个骰子的结果是 4，就有俩种方式，如果第一个骰子的结果是 1，就有俩种方式。

如果英语单词 x 和法语单词 y，z 相连接，那根据 Model 3 的生成理论，有 6 种方式会发生这样的情况。注意，这 6 种方式的可能性是一样的，因为用来相乘的因子永远都是同一个：n(3|x)，t(y|x)，t(z|x)，t(w|x)，d(1|1,1,3)，d(2|1, 1, 3)，d(3|1, 1, 3)，p₀。乘法并不关心因子的顺序。所以这里， P(a, f|e) = 6 * 所有的这些因子。

当任何单词的繁衍值超过 1 时，这第四个问题就会发生。所以我们给 P(a, f|e) 加最后一个因子，称为：

一个全新的公式诞生了！

回想一下，我们可以用 P(a, f|e) 来表示 P(f|e)：

再回想一下，我们也可以用 P(a, f|e) 来表示 P(a|e, f)：

于是，整个 Model 3 理论最终浓缩成了一个数学公式。如果你有更好的理论，也把它浓缩成了一个数学公式，那你就可以得到更好的翻译结果！

二十六、鸡生蛋还是蛋生鸡

第二十三节的点是：如果你有对齐概率，那就可以估算出参数值（通过分值计数）。第二十五节的点是：如果你有参数值，那就可以计算出对齐概率。啊哦，哪里出错了呢？

就像，要生鸡，先要有蛋。（类似这样的逻辑吧？）

二十七、见证奇迹的时刻

EM 算法（the EM algorithm）可以解决我们的问题。“EM” 的意思是“最大估计”（estimation-maximization）。也有一些人认为 “EM” 的意思是 “最大期望”（expectation-maximization）。这让我想起了之前我记不起来怎么拼写某个单词的情景：是 “intractibility” 还是 “intractability”？这俩我都用 Google 搜了下，第二个写法用 785 比 22 的比分取得了胜利。我也不知道我想表达什么，但不管怎样，EM 算法可以解决我们的问题！

让我们先给所有参数值设置一个相同的值。就是说，假设法语词典里有 40000 个单词，那对于每一组英语和法语单词，我们先假设 t(f|e) = 1 / 40000。单词 “house” 可能被翻译成 “maison”，也可能被翻译成 “internationale”。现在，我们还不知道这有什么意义。

练习题：通过把失真概率设置为同一个值，假设组里的两个句子都包含 10 个单词，那位于位置 4 的英语单词会产生位于位置 7 的法语单词的几率是多少，也就是 d(7|4, 10, 10) = ?

我们可以给 P₁ 一个随机值，比如 0.15，然后给每个英语单词一套固定的繁衍值概率。

给定刚刚这两个值，我们可以计算出两个句子的对齐概率，这意味着我们可以得到分值计数。当我们把分值计数代入计算，我们会得到另一组参数值。希望这些值是更好的，因为它们考虑到了双语语料库里数据之间的相关性。通过这些更好的参数值，我们重新计算（新的）对齐概率。从新的对齐概率里，我们可以得到更好的参数值。如果我们重复这样的操作，最后得到的参数值会很不错。

我们来看看在实际操作里它是怎样运转的。我们用一个经过大量简化的场景来构思问题。我们的语料库只包含两组句子。第一组是 bc / xy（包含两个单词的英语句子 “bc” 和包含两个单词的法语句子 “xy”）。第二组是 b / y（每一个句子只包含一个单词）。

练习题：如果我说 “只要英语单词 c 出现，法语单词 y 也跟着出现，所有它们是互译的”，你觉得怎么样？

我们也先忘掉 NULL 单词，规定每个单词的繁衍值仅为 1，也忘掉失真概率。那在这个例子中，句子组 bc / xy 就只有两种对齐方式：

练习题：在这个情景里，我们忽略了哪两种对齐方式？

句子组 b / y 就只有 1 种对齐方式：

在我们的简化下，唯一在对齐概率上的东西就是单词翻译 t 参数了。所以我们的 P(a, f|e) 公式简化成以下形式：

这其实是 Model 1 的 P(a, f|e) 公式。（虽然和这里不同的是，就算有NULL 以及所有可能的对齐方式，Model 1 通常也是有效的）

好吧，EM 是这样的：

第一步，给参数值设置成一样的值。

第二步，计算所有对齐方式的 P(a, f|e)。

第三步，代入 P(a, f|e)，得到 P(a|e, f) 的值。

对于最后一个的 b / y，只有一种对齐方式，所以 P(a|e, f) 永远是 1。

第四步，计算分值计数。

第五步，代入分值计数，得到更好的参数值。

重复第二步，计算所有对齐方式的 P(a, f|e)。

重复第三步，代入 P(a, f|e)，得到 P(a|e, f) 的值。

重复第四步，计算分值计数。

重复第五步，代入分值计数，得到更好的参数值。

重复第 2 到 5 步很多次，直到得到：

发生了什么？第二组句子 b / y 使得交叉对齐的那种方式（其中 b 和 y 相连接）的对齐概率增加了很多。这使得 t(y|b) 的值很稳固，但副作用是也使 t(x|c) 的值增加了许多，因为在那个交叉对齐中 x 与 c 相连接。t(x|c) 的增加必然导致 t(y|c) 的值被减小，因为它俩加起来等于 1。所以，即使 y 和 c 是相连接的，我们的分析说明了它们并不是互译的。

EM 算法对 Model 3 来说也是这样，除了我们用 Model 3 的公式来计算 P(a|f, e)，通过给对齐方式分配权重，我们也额外为 n，p 和 d 参数计算了分值计数。

练习题。利用 Model 1 的 EM 训练方式，对以下的句子组循环两到三次：
“the blue house” / “la maison bleue”
“the house” / “la maison”

就只认为第一组句子有 6 种对齐方式，第二组句子有 2 种对齐方式吧。开头应该是：

（译者注：后面的需要你来完成）

二十八、EM 算法在干什么？

当然，EM 算法对自然语言的翻译什么都不懂。它仅仅在尝试优化一些数值处理。这个处理是什么？要回答这个问题，我们先回到第十二节中关于对模型进行定量评估的讨论。当时我们在讨论语言模型，认为一个好的语言模型就那些会给单语测试数据大的 P(e) 值的模型。同样，一个好的翻译模型就是那些给双语测试数据大的 P(f|e) 值的模型。由于 Model 3 并没有包含一个句子与下一个句子之间的任何相关信息，我们可以认为 P(f|e) 就是在双语语料库里的所有句子组的 P(f|e) 的乘积。对 P(f|e)，我们是有一个公式的，所以这是一个量化概念。根据这个方法，Model 3 的一组参数值要么比另一组好，要么差。

参数的值都是一样的的话，计算出来的 P(f|e) 会非常小。但结果表明，EM 算法的每一次重复会保证改善 P(f|e)。这就是 EM 算法在不断优化的东西。（对于每一次计算）EM 不保证会找出全局的最佳值，但可以找出当前的最佳值。EM 算法每一次开始计算，会把上一次的计算结果作为计算中的一部分。

用困惑度来衡量一个模型的好坏会更方便：

想象下面这个赌博游戏。我向你展示一个英语句子 e，并且把对应的法语翻译藏在我口袋里。我给你 100 美元，然后你给几个不同的法语句子下注，你可以按你认为合适的方式分配这 100美元。你可以把 100 美元全部押注在一个句子上，也可以分摊在多个句子上。分配这 100 美元就像是把概率 P(f|e) 的单位质量（unit mass）分配给不同的句子 f。

然后我拿出口袋里的那个法语句子，看看你给这个句子下了多少注。如果你下注了 100 美元，你的报酬会非常丰富。即使你只下注了一点点钱，你的报酬也会很丰富。但如果你没有给这个句子下注，那你的钱就都输掉了。因为在这个情况里，你把 P(f|e) 设为 0，那你就犯了大错。

随着 EM 算法进行一次次计算，计算机会越来越来擅长这个赌博游戏。这就是它想学着做的事情，也是所有它学着做的事情。

练习题：如果你很擅长这个游戏，你认为你会擅长翻译么？如果你很擅长翻译，你会擅长这个游戏么？

在这个游戏里，Model 3 至少有两个问题。你应该都知道。第一个问题比较简单，失真参数对于翻译过程中的词序改变的描述是非常弱的。单词们换来换去，导致 Model 3 会给很多语法错误的句子下注。之前我们说过 P(e) 会负责这个遗留的问题。第二个问题是 Model 3 也会给一些你都看不出是自然语言的句子下注。在生成模型里，记住，我们给每一个法语单词提供了一个目标位置（在进行排序的步骤中）。生成模型并没有阻止我们给所有单词都提供相同的位置，比如位置 7，这样的话所有单词都会在同一个位置堆积起来，而其他位置是没有单词填入的。这样的句子是无法阅读的，因为看上去它就是一堆重合的单词，周围有大量的空白。由于 Model 3 会给这样的非句子下注，一个好的模型应该减少出现这种情况的概率。但别太过焦虑。我们不会用 Model 3 去把英语翻译为法语。而且，即使我们发现了这样的情况，我们也可以处理它——大多数的机器翻译算法会直接因此发狂，你不觉得吗？

二十九、解码（Decoding）

为了计算 P(e)，我们可以从单一的英语语料中计算出参数值。为了计算 P(f|e)，我们可以从双语语料里计算出参数值。为了翻译法语句子 f，我们寻找一个英语句子，它的这两个值的乘积是最大的。这个过程被称为解码。把所有可能的英语句子都搜索计算一遍是不可能的，但对于一组很相关的英语句子来说是可能的。本教程不会对启发式搜索（heuristic search）进行详细的介绍。IBM 扬言要在他们“即将发表的论文”（但从未发表）中介绍解码。最后在他们的美国专利书中对此进行了介绍。

三十、训练 Model 3 的一些实际问题

上面提供的训练算法还有一些问题。首先，EM 不会找到一个全局的最佳方案。在实际操作中，它可能会利用通过想象出来的单词失真规律。它可能认为优化 P(f|e) 的最佳方式是总是把任何句子组中的前两个单词连接起来。这样的话，失真的值是很小的，但单词翻译的值是很大的，因为一个英语单词会有很多可能的翻译。从语言学的角度来说，拥有小的单词翻译值和大的失真值会更合理。要解决这个问题，我们可能想把失真概率设置为一个固定的值，直到 EM 的重复计算更新了单词翻译概率。

第二个问题更严重。就像上面说的哪那样，EM 算法需要对每一组句子的每一个对齐方式进行重复计算。如果一组句子有 20 个英语单词和 20 个法语单词，可能的对齐方式会有很多种（有多少种？）。对于这样的句子组，把所有的重复计算做完是不可能的，即使是只有一组句子。

解决办法是每一次重复计算，只对那些看起来不错的对齐方式进行。比如，对于每一组句子，我们可以只收集前 100 种分值计数最高的对齐方式。这带来了两个问题。第一个，如何不使用遍历来找到最佳的 100 种对齐方式。第二个，如何去解决第一个问题。对于第一次计算，参数的值都是相同的，这意味着所有对齐方式的概率是同等的。

如果我们能用一个“快速且阴险”的方法去初始化所有的参数值，那就可以解决这两个问题。事实上，Model 1 提供了这样的方法。其实我们是可以从所有的对齐方式中获取 Model 1 的分值计数 t 的，同时不用遍历所有的对齐方式。

三十一、Model 1 的高效训练

回想一下，训练模型需要先获取分值计数，分值计数是通过 P(a|e,f) 得到的权重。也想想这个公式：

思考一下这个公式的分母。通过 Model 1，我们可以把它写成这样：

由于一共有 (l + 1)^m 种对齐方式，要评估这个公式，我们不得不计算 m * (l + 1)^m。为了清楚一点，我们用参数 t 来重写：

每一行对应一个具体的对齐方式，每一列对应一个法语单词。第一行中，所有法语单词都和 e₀（NULL）相连接。第二行是一样的，除了最后一个法语单词和 e₁ 而不是 e₀ 相连接。最后一行对应的对齐方式里，所有法语单词都和英语句子里最后的英语单词 e_l 相连接。现在你可以清晰地看出，要计算 P(f|e)，一共要进行 m * (l + 1)^m 次计算。

但在上面的公式里，我们可以找到一些可利用的规律。比如，我们可以从所有行（对齐方式）里分解出 t(f₁|e₀)：

我们省去了大量的乘法。这就类似 xy + xz（三次计算）和x(y+z)（两次计算）之间的差别。继续用这样的分解方式，我们得到：

练习题：证明这个公式和上面的公式是等同的。

用一个更紧凑的表达：

最后这个公式只需要进行两次计算（精确的说，是 (l + 1) * m 次）。这意味着，我们可以高效地为 Model 1 计算 P(f|e) 了。同理，也不难想出怎样在 EM 训练过程中高效地获取分值计数。

三十二、Model 1 的最佳对齐方式

Model 1 有另一个优点，可以很容易搞清楚对于一组句子来说，最佳对齐方式是什么（最佳对齐方式的 P(a|e,f) 值或 P(a,f|e) 值是最大的）。我们可以不用遍历所有对齐方式就做到。

记住 P(a|e,f) 是用 P(a,f|e) 来计算的。在 Model 1 中，P(a,f|e) 有 m 个因子，每个因子对应一个法语单词，每个因子看起来是这样：t(f_i|e_aj)（译者注：e_aj 是错误的写法，原文的正确写法是，a 是 e 的下标，j 是 a 的下标）。假设法语单词 f₄ 不和 e₆ 相连接，而是和 e₅ 相连接，即 t(f₄|e₅) > t(f₄|e₆)。这意味着。对于除了 f₄ 和谁相连接不同以外其余都相同的两种对齐方式，我们更倾向于 f₄ 和 e₅ 相连接的那一种——不管对齐方式里是怎么回事。所以，事实上我们可以独立地让每一个法语单词都和英语单词 “home” 相连接。

这就是最佳对齐方式，它可以通过两次运算得出：(l + 1) * m。

练习题：找出句子组“bcd/xy”的最佳对齐方式。首先遍历 9 种所有的对齐方式（不管 NULL），估算出每一种的 P(a|e,f) 值。然后用上面的两次运算，证明这两种方式的结果是相同的。使用这些参数值：t(x|b) = 0.7，t(y|b) = 0.3，t(x|c) = 0.4，t(y|c) = 0.6，t(x|d) = 0.9，t(y|d) = 0.1。

不幸的是，根据一个训练好的 Model 1，“最佳”对齐方式可能看上去不会令人满意。因为每一个法语单词独立地选择了它觉得对的英语单词“home”，它们非常有可能都选择了英语单词 e₅。根据 Model 1 的生成理论（我没给你写出来），意味着 e₅ 把所有法语单词都生成了。

三十三、回到 Model 3

我们的语言直觉告诉我们，e₅ 不太可能生成所有的法语单词。事实上，Model 3 会用繁衍值概率来惩罚这样的对齐方式。如果 e₅ 不太可能有这么高的繁衍值，同时其他单词的繁衍值不太可能同时为 0，那这样的对齐方式会很差。Model 1 并没有应对此问题的方式。

看的出来“繁衍值”的概率是来自语言直觉。当然，这些直觉必须经过测试。在真实的翻译中，繁衍值可能会是很随机的值，通过各自的最佳对齐方式，我们总是可以比较 Model 1 和 Model 3，来看看谁会是更好的。我们也可以通过各自的困惑度（参考第二十节）来比较这些模型。

对于翻译模型来说，繁衍值可能有不错的效果，但对高效计算来说就不是了。我们不能用第三十二节中的妙招来计算 Mode 3 的最佳对齐方式，因为法语单词是不能独立地选择各自的翻译的，如果两个单词同时选择了“home”，整个 P(a, f|e) 值可能都会被改变。况且，我们必须遍历所有的对齐方式才能计算 P(f|e)。第三十一节中的分解方式也不能用。也不是毫无希望：我们至少可以用第二十五节中的公式来比较快速地计算某个特定对齐方式的 P(a, f|e)。

对于 Model 3 的训练，有一个实际可行的方案。首先，我给你看一个图，然后解释它。

好吧：我们首先用几个重复步骤来训练 Model 1。之后，通过 Model 1 的参数值，我们就找到了每组句子的最佳对齐方式（也称为维特比对齐（Viterbi alignment））。对于每一组句子，我们用 Model 3 的 P(a,f|e) 公式来重新给 Model 1 的维特比对齐计算分数。（在 Model 3 的第一次重复中，我们必须给所有的繁衍值概率和所有的失真概率都分别设置为一个相同的值）

一旦我们得出一个合理的对齐方式和 Model 3 给的分数，就可以给这个对齐方式尝试一些小的调整（比如，把 f₄ 连接到 e₇ 而不是 e₅），如果这样的调整使得 Model 3 给出的分数更高，我们就采用这个调整。我们不断调整这个对齐方式（像爬山一样），直到再也不能继续优化。我们把最后的这个对齐方式称为 Model 3 的维特比对齐。

Model 3 的维特比对齐和它的邻居（neighborhood）——那些可以通过调整维特比对齐而得到的对齐方式，是 Model 3 所有对齐方式中比较合理的一个子集。我们可以只对这个子集计算分值计数。当我们代入这些数值的时候，就可以得到新的 t，n，d 和 p 值，我们可以不断重复此操作。再说一遍，通过 Model 1 和 t 值，我们拿到了最佳对齐方式，这些对齐方式，我们可以贪婪地找到 Model 3 的最佳对齐方式。注意，把新的 t 值代入 Model 1 可能得出一个新的 Model 1 的最佳对齐方式。

如果有一组更大的看起来不错的对齐方式，我们可以“同时爬多个山”——每一个都从 Model 1 的维特比对齐的一个变种开始，在这个变种中，某一条连接是我们手动设置的。

三十四、Model 2

最后，我们来做一个略微不同但很有意思的事情。你应该知道 Model 2 的存在吧？这个模型考虑到了单次翻译（和 Model 1 一样，同时也考虑到了失真值。和 Model 1 一样，我们可以找出维特比对齐，也可以高效地计算出分值计数。Model 2 中的失真概率和 Model 3 的有些不同。我们用反向失真概率：

a(英语位置|法语位置，法语句子长度，英语句子长度)

而不是

d(法语位置|英语位置，英语句子长度，法语句子长度)

我很抱歉在这里大量使用符号 a，因为我意识到 a 更适合用来表示对齐方式（alignment）。非常，非常抱歉。如果有什么补偿是我能做的，请告诉我。Model 2 的 P(a, f|e) 公式是：

这个模型会惩罚那些连接非常远的位置的对齐方式，即使被连接的单词是相互翻译的。或者说在训练中，它更倾向于在位置的基础上，连接那些实际上是互译的的单词。（没有足够的单词共现来建立可靠的单词翻译概率）

要找到 Model 2 的最佳对齐方式，我们为每个法语单词 f_i 独立地选择一个英语位置 i，这个位置是单词翻译和失真值因子的最大值：

要高效地计算 P(f|e)，我们用分解的方式来重写：

练习题：说服你自己，这个重写是正确的。

我们不难将这个推理拓展到为句子组高效计算分值计数的算法中去。

三十五、将参数值从一个模型迁移到另一个模型

我们可以直接跳过 Model 1，把 Model 2 运用到句子组语料库中。我前面说过，在考虑失真值之前，给单词翻译概率先设置一些合理的值会更好。所以我们先用 Model 1 重复几次计算，把最终得到的 t 值作为 Model 2 第一次计算的输入，而不是也设置一个相同的 t 值。这个简单的概念被称为参数值迁移（transferring parameter values）。

当我们从 Model 2 迁移参数值到 Model 3 的时候更有意思。我们可能会用从 Model 2 重复计算中得到的一切来初始化 Model 3 的参数值。虽然我们可以给 d 值的二维表都设置为同一个值，但设置一个更好的值并不难。我们可以在 Model 2 的重复计算和 Model 3 的重复计算中插入一个重复计算的“一次性”特殊迁移。在这个迁移过程中，我们可以做两次运算来得到分值计数，除了可以算出 t 值和 a 值，我们也可以算出 d 值。

繁衍值呢？我们可以在初始化时设置一些相同的值，但，重复一遍，我们也可以用 Model 2 里得到的东西来设置更好的初始化值。想象一下，Model 2 会识别出一些很高概率的对齐方式。这样的话，我们可以检查这些对齐方式来得到一个比较合理的单词（比如 “house”）的繁衍值。如果，根据 Model 2，“house” 倾向于只连接一个法语单词，那我们可以总结出它的繁衍值可能是 1。当然，Model 3 接下来的重复计算可以改变这个结论。

不幸的是，把 t 和 a 转换成繁衍值（n）并没有一个可用的二次计算。我们必须放弃遍历所有对齐方式的想法。但有一个妥协的办法。

为了解释它，我们先忘掉 a 参数（反向失真参数），仅仅从 Model 1 中得到的 t 参数来初始化参数值。对于包含句子组 bc/xy 的语料库，假设从 Model 1 得到了以下值：

我们假设有下面四种可能的对齐：

现在我们想猜测出繁衍值二维表 n 的初始值。我们来看看这四种方法。

方法一：设置相同的概率值。我们从对齐方式中看出，单词 b 可能有繁衍值 0，1 或 2。因此我们赋值 n(0|b) = n(1|b) = n(2|b)。

方法二：从所有对齐方式中算出分值计数，但先假设所有对齐方式都是同等可能的。在四种对齐方式里，只有第 2 种对齐方式里的单词 b 的繁衍值是 0，所以 n(0|b) = 1/4。这个方法可以高效地运用到非常长的句子组中去。

练习题：如果使用这个方法，n(1|b) 和 n(2|b) 的值是多少？这个结果你觉得有意义么？

方法三：从所有对齐方式中算出分值计数，但把单词翻译考虑进去。这和正常的 EM 训练差不多。对于每一个对齐方式，我们计算出 P(a|e,f)，然后用它来给我们收集到的次数给权重。记住，

对 Model 1 来说， P(a,f|e) 是当前对齐方式的所有单词翻译概率的乘积。

译者注：alignment意思是对齐方式，normalized意思是

练习题：P(alignment₄|e,f) 是什么？

现在我们来计算分值计数。第 2 种对齐方式是唯一单词 b 的繁衍值是 0 的对齐方式，所以我们用权重 0.16 来计算 0 的繁衍值次数：

第 1 和第 4 种对齐方式里，单词 b 的繁衍值是 1，所以我们得到两个分值计数：

在这里，nc 次数的值刚好已经加了 1，所以在代入中他们保持了不变。0.16/0.68/0.16 的分布比从方法一和方法二中得到的要好，因为它考虑到了 Model 1 的计算结果，即第 1 种对齐方式是非常高概率的，以及这两个单词的繁衍值有可能是 1。

方法四：我们知道方法三并不适用于很长的句子组，因为我们不可能遍历所有的对齐方式。但我们从方法三中得到的结果和便宜算法的结果是完全一致的。（参考后面的图 1）

你可以手动证明对于上面的例子这个算法得到的结果和方法三是完全一致的。通过把上面公式里的每一个 t(f_i|e_i) 额外乘一个因子 a(i|j,l,m)，这个方法就可以用在 Model 2 身上。方法四的证明可以在（Brown 等人于 1993年）方程 108 后面找到。注意，这个方程有一个错误（请从 α 的计算中移除因子 k!）。最后，有一个不错的办法，在线性时间内遍历整数的分区，同时不用给每一个分配内存。几乎就像我是一个时髦的年轻人一样，我在网上找到了一些可以实现这个的 Pascal 代码。（译者注：作者是在讽刺现在的年轻人吗？）

你可能会想：如果我们可以计算繁衍值的次数，同时不用遍历所有的对齐方式，那我们不是已经解决了不启发式地依赖于对齐方式子集从而实现对 Model 3 进行训练的问题吗。并没有完全解决。上面的方法用 t 和 a 值来计算繁衍值。如果我们尝试重复这个操作，会不得不抛弃繁衍值——我们刚刚算出来的！唯一的输入是 t 和 a。这个方法不能接受一组繁衍值，然后优化它们，这是我们想从 Model 3 的训练中得出的。

用类似的方法来给 p₁ 参数取初始值是有可能的，但我建议你就随便给个值，然后开始优化它。

l = 英语句子长度
m = 法语句子长度
e_i = 第 i 个英语单词
f_j = 第 j 个法语单词
t(f|e) = 英语单词 e 被翻译成法语单词 f 的概率
φ_max = 所有单词的繁衍值中的最大值
Γ(n) = 所有大于等于 1 的整数之和（比如，1+2+4 是 7 的一个分区，1+1+1+1+3 也是）
次数(分区,k) = 在分区中整数 k 出现的次数

图 1

三十六、最终的训练方案

在这个新的方案里，我们将在 Model 2 和 3 之间插入 Model 2 的重复计算，以及一个重复计算的“一次性”特殊迁移。要给 Model 3 训练计算一组最佳对齐方式，我们用 Model 2 的维特比对齐作为开始，然后用它来贪婪地搜索 Model 3 的“维特比”对齐（引号的意思是它其实不是真正意义上的最佳对齐方式，但它是我们能快速找到的最佳对齐方式）。然后我们收集所有合理的相邻对齐方式。

注意，即使在 Model 3 的重复计算过程中，我们也会不断优化更改参数 a 的值（反向失真），因为 Model 3 需要把 Model 2 的结果作为计算的一部分。

三十七、哇哦！

在这个质数（prime-numbered）小节，我们要画上句号了。如果你一路坚持下来，那我请你喝啤酒！

译者：
正文已结束。

译文：统计机器翻译教程——正文二