LibreOJ #6001. 「网络流 24 题」太空飞行计划

\(\quad\) 与网络流有关的最值有三个：最大流，最小费用，最小割。这道题是最小割。想了好久，终于想明白最小割应该怎么用。
\(\quad\) 先找出矛盾的事物。在这道题中，两件事是矛盾的：做实验 \(E_i\) 和不取\(E_i\) 要求的任意一个器材 \(I_j\)。上面的 \(5\) 个点依次表示做实验 \(E_1, E_2,...,E_5\)，下面的 \(5\) 个点依次表示不取器材 \(I_1,I_2,...,I_5\)。（当然，实际情况中实验个数和器材个数不一定相等）

\(\quad\) 初始情况下，每个点都存在。其中，上面的 \(5\) 个点提供了 \(\sum_{i=1}^5p_i\) 的收益，下面的 \(5\) 个点提供了 \(0\) 的收益。这样的情况是非法的，因为它允许了一些矛盾的点存在。比方说，\(E_5\) 要求的器材有 \(I_3\)，那么做 \(E_5\) 和不取 \(I_3\) 这两个点就是矛盾的，不能共存。

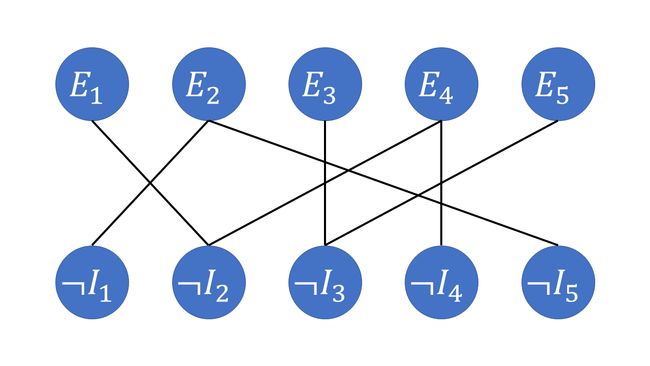
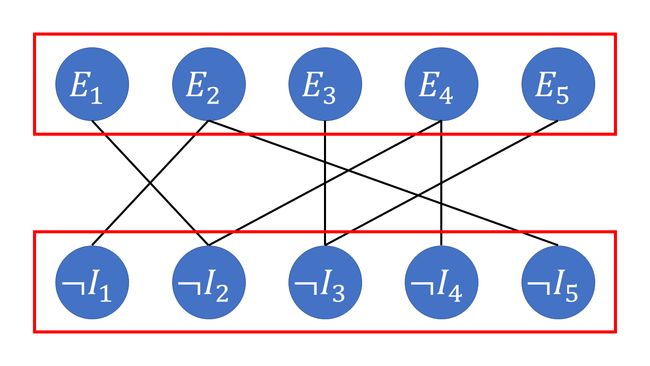
\(\quad\) 用连线来表示这种矛盾关系：有边相连的两个点是矛盾的。为了使情况合法，必须去掉一些点。去掉点有代价，比如，去掉不取 \(I_3\) 就是取 \(I_3\)，代价为 \(I_3\) 的价格 \(c_3\)；去掉做 \(E_2\) 的代价就是就是 \(E_2\) 的利润 \(p_2\)。我们的目的是使任意一条连线的两边都至多存在一个点，代价最小。换言之，要求通过删去一些点使得图的上半部分与下半部分不联通。

\(\quad\) 这就可以加上源点汇点，转换为图的最小割了。其中，\(t\) 与 \(E_i\) 的边的容量是去掉它的代价，即 \(p_i\)；\(s\) 与 不取 \(I_i\) 的边的容量是去掉它的代价，即 \(c_i\)。其余边容量为 \(+\infty\)。

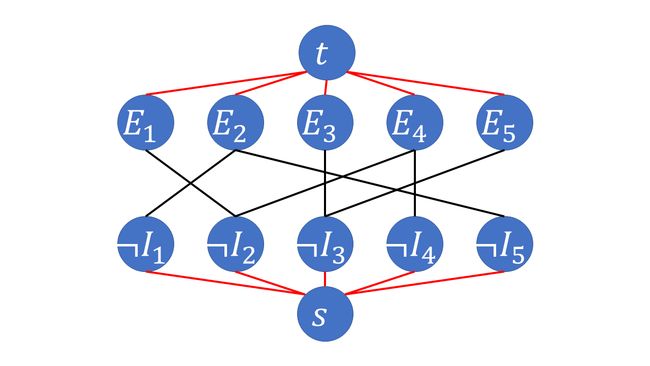
\(\quad\) 删去一条红边就代表删去对应的点；图的最小割就是最小代价。

#include 
#include 
#include 
#include 

std::string str;
int it;
#define getchar() str[it++]

int read(void){
    if(it == str.length())
        return EOF;
    int res = 0; char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(it == str.length())
            return EOF;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        res = res * 10 + ch - 48;
        if(it == str.length())
            return res;
        ch = getchar();
    }
    return res;
}

const int MAXN = 3e2 + 19, MAXM = MAXN * MAXN + MAXN + MAXN, INF = 0x3f3f3f3f;

struct Edge{
    int to, next, c;
}edge[MAXM];

int cnt = -1, head[MAXN];

inline void add(int from, int to, int c){
    edge[++cnt].to = to;
    edge[cnt].c = c;
    edge[cnt].next = head[from];
    head[from] = cnt;
}

int m, n;
int ans, c, p;

int dep[MAXN];

int bfs(void){
    std::queueq; q.push(0);
    std::memset(dep, 0, sizeof dep); dep[0] = 1;
    while(!q.empty()){
        int node = q.front(); q.pop();
        for(int i = head[node]; i != -1; i = edge[i].next)
            if(!dep[edge[i].to] && edge[i].c)
                dep[edge[i].to] = dep[node] + 1, q.push(edge[i].to);
    }
    return dep[n + m + 1];
}

inline int min(const int& a, const int& b){
    return a < b ? a : b;
}

int dfs(int node, int flow){
    if(node == n + m + 1 || !flow)
        return flow;
    int stream = 0, f;
    for(int i = head[node]; i != -1; i = edge[i].next)
        if(dep[edge[i].to] == dep[node] + 1 && (f = dfs(edge[i].to, min(flow, edge[i].c)))){
            flow -= f, stream += f;
            edge[i].c -= f, edge[i ^ 1].c += f;
            if(!flow)
                break;
        }
    return stream;
}

int dinic(void){
    int flow = 0;
    while(bfs())
        flow += dfs(0, 0x3f3f3f3f);
    return flow;
}

int main(){
    std::memset(head, -1, sizeof head);
    std::cin >> m >> n; std::getline(std::cin, str);
    for(int i = 1; i <= m; ++i){
        std::getline(std::cin, str); it = 0;
        ans += (p = read());
        add(0, i, p), add(i, 0, 0);
        int u;
        while((u = read()) != EOF)
            add(i, m + u, INF), add(m + u, i, 0);
    }
    for(int i = 1; i <= n; ++i){
        std::cin >> c;
        add(m + i, m + n + 1, c), add(m + n + 1, m + i, 0);
    }
    ans -= dinic();
    for(int i = 1; i <= m; ++i)
        if(dep[i])
            std::printf("%d ", i);
    std::putchar('\n');
    for(int i = 1; i <= n; ++i)
        if(dep[m + i])
            std::printf("%d ", i);
    std::putchar('\n');
    printf("%d\n", ans);
    return 0;
}

行末空格真的烦...