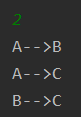第一场
官方题解:https://ac.nowcoder.com/discuss/364600?type=101&order=time&pos=&page=3
Problem A
https://ac.nowcoder.com/acm/contest/3002/A
自己在做这个规律时候特别难找,不知道怎么分类,还有重复的问题,通过抄答案学习一下分类方法。
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
int main(){
lli n,m;
lli ans=0;
cin>>n>>m;
ans=(n-2)*(m-1)*4%mod+(n-1)*(m-2)*4%mod; // 两条边分别和x轴和y轴平行的部分
ans=(ans+2*(n-1)*(m-2)%mod*(m-2)%mod+2*(m-1)*(n-2)%mod*(n-2)%mod)%mod;//底边为2分别与x,y轴平行,不含两条边都和x,y轴平行
ans=(ans+2*(n-2)*(m-1)%mod*(m-2)%mod+2*(m-2)*(n-1)%mod*(n-2)%mod)%mod;//底边为1分别与x,y轴平行,不含两条边都和x,y轴平行
cout< Problem B
https://ac.nowcoder.com/acm/contest/3002/B
快速完成。
Problem D
https://ac.nowcoder.com/acm/contest/3002/D
快速完成。
Problem E
https://ac.nowcoder.com/acm/contest/3002/E
每一个数的因数是对称的,排除掉相同的就是答案了。
#include
using namespace std;
typedef long long int lli;
lli isPrime(lli num){
double sqrtnum = sqrt(num*1.0);
for (int i = 2; i <= sqrtnum; i++){
if (num %i == 0) return 0;
}
return 1;
}
int main(){
lli n;
lli ans=0;
int Prime;
cin>>n;
Prime=isPrime(n);
if(Prime==1){
cout<<1< Problem G
https://ac.nowcoder.com/acm/contest/3002/G
记录双队列的序号,维护这个双队列,找最小值。
#include
using namespace std;
typedef long long int lli;
int main(){
queue a[27];
lli n,k,min;
bool exist=false;
cin>>n>>k;
min=n;
char x;
for(lli i=1;i<=n;i++){
cin>>x;
if(a[x-96].size()==k){
a[x-96].pop();
}
a[x-96].push(i);
if(a[x-96].size()==k){
exist=true;
if(a[x-96].back()-a[x-96].front() Problem H
https://ac.nowcoder.com/acm/contest/3002/H
#include
using namespace std;
typedef long long int lli;
lli n,k;
string a;
lli answer(char x){
lli len=a.length();
lli ans=0,j=0,num=0;
for(lli i=0;ik){
if(a[j]!=x) num--;
j++;
}
}
ans=max(ans,i-j+1);
}
return ans;
}
int main(){
lli ans;
cin>>n>>k>>a;
ans=max(answer('1'),answer('0'));
if(ans>n) ans=n;
cout< 第二场
官方题解:https://ac.nowcoder.com/discuss/364961?type=101&order=0&pos=13&page=3
Problem A
https://ac.nowcoder.com/acm/contest/3003/A
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
int main(){
lli a,b,c,x,y,z;
lli ans=0;
cin>>a>>b>>c>>x>>y>>z;
if(y>a) ans+=a;
else ans+=y;
if(z>b) ans+=b;
else ans+=z;
if(x>c) ans+=c;
else ans+=x;
cout< Problem B
https://ac.nowcoder.com/acm/contest/3003/B
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
int main(){
lli s,num1=0,num6=0;
char temp;
lli ans=0;
cin>>s;
while(s--){
cin>>temp;
if(temp-48==1) num1++;
if(temp-48==6) num6++;
if(num1>=1&&num6>=2){
ans++;
num1-=1;
num6-=1;
}
}
cout< }
Problem C
https://ac.nowcoder.com/acm/contest/3003/C
一个dp问题 有写的好的题解:https://ac.nowcoder.com/acm/problem/blogs/200167
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
lli a[2300]={0};
lli ans[2300][2300]={0};
int main(){
lli n;
cin>>n;
ans[0][0]=1;
for(int i=1;i<=n;i++){
cin>>a[i];
ans[i][0]=ans[i-1][0]*(mod+1-a[i])%mod;//求有i道题目做对0道题目的概率
for(int j=1;j<=i;j++){
ans[i][j]=(ans[i-1][j]*(mod+1-a[i])%mod+ans[i-1][j-1]*a[i])%mod;
//由类推求出当前有i道题目中,做对j道题目的概率
//这里j从1开始进行枚举到当前循环下的i,
//所以在这个过程中就求出来了有i题的情况下,做对0到i道题目的概率
}
}
//输出检查
// for(int i=0;i<=n;i++){
// for(int j=0;j<=n;j++){
// cout< Problem D
https://ac.nowcoder.com/acm/contest/3003/D
本题要注意不能先相加再判断,防止爆long long int
#include
typedef long long int lli;
const lli mod=1e9+7;
using namespace std;
lli coordinate[510][3]={0};
lli GetL2(lli x1,lli y1,lli x2,lli y2){
lli temp;
temp=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
return temp;
}
int main(){
lli n;
lli a=0,b=0,c=0;
lli ans=0;
cin>>n;
for(lli i=1;i<=n;i++) scanf("%lld %lld",&coordinate[i][1],&coordinate[i][2]);
for(lli i=1;i<=n-2;i++){
for(lli j=i+1;j<=n-1;j++){
for(lli k=j+1;k<=n;k++){
if((coordinate[j][1]-coordinate[i][1])*(coordinate[k][2]-coordinate[j][2])==(coordinate[k][1]-coordinate[j][1])*(coordinate[j][2]-coordinate[i][2])) continue;
a=GetL2(coordinate[i][1],coordinate[i][2],coordinate[j][1],coordinate[j][2]);
b=GetL2(coordinate[j][1],coordinate[j][2],coordinate[k][1],coordinate[k][2]);
c=GetL2(coordinate[i][1],coordinate[i][2],coordinate[k][1],coordinate[k][2]);
if((a+b==c)||(b+c==a)||(a+c==b)) continue;
if(a>b&&a>c) swap(a,c);
if(b>c&&b>a) swap(b,c);
if(a+b Problem G
https://ac.nowcoder.com/acm/contest/3003/G
本题卡模数,还没清楚怎么解决
#include
using namespace std;
const int mod[] = {2, 3, 5, 7, 11, 31, 71, 97, 233, 397, 433, 449, 607, 857, 10007, 21179, 36251, 44579, 62003, 72883, 97843, 139991, 232013, 369353, 681521, 692711, 777241, 822821, 1956761, 2145137, 2915837, 6229117, 7788787, 13743493, 17331841, 19260817, 19269293, 19959809, 21006959, 23937083, 24410849, 28452757, 28478603, 29229359, 35570827, 35604011, 35875487, 37370863, 38303347, 38475517, 38819149, 40455791, 44021539, 45641993, 46531301, 48866749, 50529641, 52634191, 52790587, 55180799, 56971613, 58259351, 60954737, 62207269, 63367453, 65072599, 66017821, 67952779, 69475349, 74689217, 77059907, 77907121, 79391659, 84768797, 85584601, 85724879, 85756609, 86850899, 91783511, 92331541, 94519499, 96375241, 99033413, 99486311, 100569829, 106873549, 109329881, 109913681, 111186487, 111894067, 112136617, 112417363, 114011921, 119143363, 122994493, 123747781, 124001021, 126515639, 128191039, 128767909, 132222763, 133587661, 139644719, 145641527, 153388423, 155187077, 156883333, 157989581, 159538063, 161488643, 164039129, 166070447, 169181543, 169554227, 173564801, 175742867, 185469637, 187203899, 191263223, 198691817, 204144887, 211631201, 217903877, 218028203, 220073423, 228143453, 228667423, 232064653, 240519263, 245647159, 247586411, 247936121, 250949197, 253413211, 253464329, 260572729, 260590409, 262887773, 265711423, 266763641, 273585149, 276472817, 276500531, 280543667, 280649591, 281385491, 291366337, 293273159, 296973107, 302890501, 306568693, 315614297, 316729409, 317617121, 320337781, 320613497, 321322823, 324691051, 325963067, 327184157, 329900633, 330670159, 332058781, 332213669, 332300869, 334382221, 341895677, 347938237, 349011827, 349347503, 349906439, 353796941, 364557253, 364755931, 367946441, 372413831, 374358983, 379589897, 381149689, 389431873, 404683493, 405216109, 405495029, 408142403, 408989747, 410841979, 410935093, 412405351, 412592459, 412722139, 412990573, 418171483, 421270357, 424233613, 427938449, 428492083, 429962881, 430883569, 434988383, 435941201, 438816151, 440052953, 440143589, 444693631, 453646433, 455847109, 456640189, 457911511, 458185237, 463116761, 463861417, 469275953, 471298573, 471712513, 478267417, 483824813, 494828483, 497397293, 499657393, 507957479, 512906621, 519346459, 519879973, 520094713, 523213693, 525673273, 529575763, 529883803, 533887031, 534260809, 535328309, 541992667, 542253071, 544780177, 545567609, 552922529, 555129893, 555820037, 558473471, 563484017, 571310471, 578121241, 582251063, 583825639, 584121323, 592038487, 599098811, 601467677, 610073969, 615059213, 619220713, 622457177, 627412609, 630547919, 632342989, 637357363, 638865419, 648268013, 650007487, 651564761, 654115433, 661281713, 662664461, 667914281, 682988213, 691099121, 691445809, 692038043, 692411953, 698620943, 699007259, 701164631, 706806461, 707096251, 707697451, 709566589, 719095829, 725756807, 736880491, 739603867, 743026709, 744236861, 744396049, 747393791, 749395103, 760341121, 762934307, 773124059, 773195911, 776162609, 781629113, 781884613, 786120631, 788314343, 788898377, 788939293, 790209983, 791933183, 796328783, 798643889, 802280047, 803293991, 803847559, 809752739, 818520473, 820434047, 826810489, 829359959, 829707427, 836587463, 841011167, 843763253, 849410557, 851226437, 853058471, 853168793, 853778327, 859086391, 860720017, 863193077, 873061181, 888803059, 893035529, 900902953, 904636883, 917949577, 921817139, 922328707, 931449133, 933074827, 933156233, 935241721, 935632799, 939948881, 957119773, 961329913, 965269573, 965337949, 967551691, 971080093, 973578143, 976825877, 985100197, 985413691, 986124823, 990650057, 998244353, 999058883, 1000000007};
int ff(int a, int m) {
return (a % m + m) % m;
}
int Pow(int a, int b, int c) {
int ret = 1;
while (b) {
if (b & 1) ret = ret * 1ll * a % c;
a = a * 1ll * a % c;
b >>= 1;
}
return ret;
}
int a, b, c, d, e, f, g;
bool check(int m) {
return ((Pow(ff(a, m), d, m) + Pow(ff(b, m), e, m)) % m + Pow(ff(c, m), f, m)) % m == ff(g, m);
}
int main() {
int T;
cin >> T;
while (T--) {
// cerr << T << endl;
cin >> a >> b >> c >> d >> e >> f >> g;
assert((a || d) && (b || e) && (c || f));
assert(min(a, min(b, min(c, g))) >= -1e9 && max(a, max(b, max(c, g))) <= 1e9 && min(d, min(e, f)) >= 0 && max(d, max(e, f)) <= 1e9);
bool flag = 1;
for (int i = 0; i < 349; ++i) if (!check(mod[i])) {flag = 0; break;}
puts(flag ? "Yes" : "No");
}
return 0;
} 第三场
官方题解:https://ac.nowcoder.com/discuss/365306?type=101&order=time&pos=&page=1
1s 一亿次
Problem A
https://ac.nowcoder.com/acm/contest/3004/A
在他人帮助下的第一个?(大概)的DP(大概)题。
一个没想到:使用另一个的同样大小的二维数组保存答案
注:此方法还可优化为一个三行数组。
注意到,题目给出的迷宫的走法规则,后一步的行为对前一步得出的结果没有影响,于是可以写出递推式。
遍历输入数组的每一个格子,在不越界的情况下:
初值条件:ans0=1
可以从左上到达的格子:此格子里的数(走法)等于上格子加左格子
ansi=ansi-1+ansi
可以从左面到达的格子:此格子里的数(走法)等于左格子
ansi=ansi
可以从上方到达的格子:此格子里的数(走法)等于上格子
ansi=ansi-1
#include
#include
#define MOD (long long)(1e9+7)
using namespace std;
int n,m;
char s[51][51];
long long ans[51][51];
int main()
{
scanf("%d%d",&n,&m);
for(register int i=0;i=0&&s[i-1][j]!='R')
ans[i][j]=(ans[i][j]+ans[i-1][j])%MOD;
if(j-1>=0&&s[i][j-1]!='D')
ans[i][j]=(ans[i][j]+ans[i][j-1])%MOD;
}
}
//验证答案图
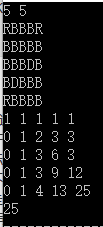
// for(register int i=0;i Problem I
https://ac.nowcoder.com/acm/contest/3004/I
汉诺塔的总移动数 Sum =2^n -1
观察前述移动的规律:
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
lli sum=0;
lli ans[61][7];
int main(){
lli n;
cin>>n;
//hanoi(n,'A','B','C');
ans[1][1]=0;
ans[1][2]=1;
ans[1][3]=0;
ans[1][4]=0;
ans[1][5]=0;
ans[1][6]=0;
for(lli i=2;i<=n;i++){
ans[i][1]=0;
ans[i][2]=0;
ans[i][3]=0;
ans[i][4]=0;
ans[i][5]=0;
ans[i][6]=0;
ans[i][1]+=ans[i-1][2];
ans[i][2]+=ans[i-1][1];
ans[i][3]+=ans[i-1][5];
ans[i][4]+=ans[i-1][6];
ans[i][5]+=ans[i-1][3];
ans[i][6]+=ans[i-1][4];
++ans[i][2];
ans[i][1]+=ans[i-1][3];
ans[i][2]+=ans[i-1][4];
ans[i][3]+=ans[i-1][1];
ans[i][4]+=ans[i-1][2];
ans[i][5]+=ans[i-1][6];
ans[i][6]+=ans[i-1][5];
}
//1ab 2ac 3ba 4bc 5ca 6cb
cout<<"A->B:"<C:"<A:"<C:"<A:"<B:"< 第四场
官方题解:https://ac.nowcoder.com/discuss/365889?type=101&order=time&pos=&page=3
Problem A
https://ac.nowcoder.com/acm/contest/3005/A
找规律发现gcd(1,0)——gcd(1,1)——..... 最小
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
int main(){
int T,n;
lli a=2,b=1,sum;
cin>>T;
while(T--){
cin>>n;
a=2,b=1;
if(n==0){
cout<<1< Problem B
https://ac.nowcoder.com/acm/contest/3005/B
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
string s;
int main(){
cin>>s;
stack temp;
int n=s.length();
for(int i=0;i 第五场
官方题解:https://ac.nowcoder.com/discuss/366644?type=101&order=time&pos=&page=3
Problem A
https://ac.nowcoder.com/acm/contest/3006/A
#include
using namespace std;
typedef long long int lli;
char a[100050];
char b[100050];
int main(){
int n,m,ans=0;
int len;
cin>>n>>m;
cin>>a; cin>>b;
len=min(n,m);
for(int i=0;i Problem E
https://ac.nowcoder.com/acm/contest/3006/E
发现——当2的n次方时,没有必胜策略
对小于10的18次方的所有数进行打表,对输入的所有数进行判断即可
#include
using namespace std;
typedef long long int lli;
lli a[100000];
int is2n2(lli x){
lli a[]={2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072,262144,524288,1048576,2097152,4194304,8388608,16777216,33554432,67108864,134217728,268435456,536870912,1073741824,2147483648,4294967296,8589934592,17179869184,34359738368,68719476736,137438953472,274877906944,549755813888,1099511627776,2199023255552,4398046511104,8796093022208,17592186044416,35184372088832,70368744177664,140737488355328,281474976710656,562949953421312,1125899906842624,2251799813685248,4503599627370496,9007199254740992,18014398509481984,36028797018963968,72057594037927936,144115188075855872,288230376151711744,576460752303423488,1152921504606846976};
for(int i=0;i<60;i++){
if(a[i]==x) return 1;
}
return 0;
}
int main(){
lli n;
cin>>n;
if(n==2){
cout<<"Alice";
return 0;
}
if(n%2!=0){
cout<<"Bob";
return 0;
}
else{
if(is2n2(n)) cout<<"Alice";
else cout<<"Bob";
}
return 0;
} Problem I
#include
using namespace std;
typedef long long int lli;
lli a[100000];
int main(){
int n;
double m;
lli proi;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
proi=a[9];
if(proi>=0.8*m){
cout<<"Yes";
return 0;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n-i;j++){
if(a[j]=a[3]) cout<<"Yes";
else cout<<"No";
return 0;
} Problem J
https://ac.nowcoder.com/acm/contest/3006/J
使用泰勒公式计算出cos值,使用余弦定理计算出角的对边的值。
#include
using namespace std;
typedef long long int lli;
#define pi 3.1415926535898
double funcos( double e, double x ) {
double eps,sum,term,a;
double sign=1;
double k=0;
unsigned long long n=1;
eps=e;
sum=0;
term=10000;
a=x;
while(fabs(term)>=eps){
x=pow(x,k);
term=x/n;
x=a;
sum=sum+(term*sign);
sign=-sign;
k=k+2;
n=1;
for(int i=1;i<=k;i++){
n=n*i;
}
}
return sum;
}
int main(){
double n,r;
double x,L;
lli i,j;
cin>>n>>r;
cin>>i>>j;
x=2.0*pi/(n*1.0);
// printf("%.9lf\n",funcos(0.000000001,x));
L=2.0*(r*1.0)*(r*1.0)-2.0*(r*1.0)*(r*1.0)*funcos(0.000000001,x);
L=sqrt(L);
// printf("%.6lf\n",min(fabs(i-j),n-fabs(i-j)));
printf("%.6lf",min(fabs(i-j),n-fabs(i-j))*1.0*L);
return 0;
} 第六场
官方题解:https://ac.nowcoder.com/discuss/367149?type=101&order=time&pos=&page=2
Problem A
https://ac.nowcoder.com/acm/contest/3007/A
分别将前k大的数,一个集合第i小的和另一个集合第i大的
配对,得出k个数最后最小的那个数就是答案。
#include
using namespace std;
const int N = 100050;
int a[N], b[N], n, k, ans = 2e8;
int main()
{
int i, j;
scanf("%d%d", &n, &k);
for(i = 1; i <= n; i ++)
scanf("%d", &a[i]);
for(i = 1; i <= n; i ++)
scanf("%d", &b[i]);
sort(a + 1, a + n + 1);
sort(b + 1, b + n + 1);
for(i = n; i > n - k; i --)
ans = min(ans, a[i] + b[(n - k )+ (n + 1 - i)]);
printf("%d\n", ans);
return 0;
} Problem F
可以在O(N)的时间内计算出答案
每一个十字阵列的总数可以用通式表达
An=((ni+mj)+((1+n)n/2)+((1+m)m/2)-(i+j))*w;
#include
using namespace std;
typedef long long int lli;
typedef long long ll;
#define mod (1000000007)
lli gcd(lli a,lli b){
return b>0?gcd(b,a%b):a;
}
inline ll read(){
char ch = getchar();
ll p = 1,data = 0;
while(ch<'0'||ch>'9'){
if(ch == '-')
p = -1;
ch = getchar();
}
while(ch>='0'&&ch<='9'){
data = (data<<3)+(data<<1)+ch-'0';
ch = getchar();
}
return p*data;
}
int main(){
lli m,n,h;
lli i,j,w;
lli k;
lli sd=0;
m=read();n=read();h=read();
k=n+m-1;
while(h--){
i=read();j=read();w=read();
sd+=((n*i+m*j)+((1+n)*n/2)+((1+m)*m/2)-(i+j))*w;
sd=sd%mod;
}
cout< Problem G
https://ac.nowcoder.com/acm/contest/3007/G
将括号序列匹配的代码稍微更改一下就得到了有多少错误的括号排布
Sum=While(stack_empty){+1}+stack_size
#include
using namespace std;
typedef long long int lli;
const lli mod=1e9+7;
string s;
lli ans=0;
int main(){
lli t,n;
scanf("%lld",&t);
while (t--){
scanf("%lld",&n);
cin>>s;
stack temp;
for(register lli i=0;i Problem J
https://ac.nowcoder.com/acm/contest/3007/J
满足以下条件即可,设能构成三角形的三边A,B,C
R1+R2=A
R2+R3=B ————存在
R1+R3=C
#include
using namespace std;
typedef long long int lli;
lli gcd(lli a,lli b){
return b>0?gcd(b,a%b):a;
}
lli a[30]={0};
int main(){
lli a,b,c;
double r1,r2,r3;
scanf("%lld%lld%lld",&a,&b,&c);
if(a+b<=c||b+c<=a||a+c<=b) {
printf("wtnl\n");
return 0;
}
r1=(a+c-b)*1.0/2.0;
r2=(a+b-c)*1.0/2.0;
r3=(b+c-a)*1.0/2.0;
if(r1==0||r2==0||r3==0){
printf("No\n");
return 0;
}
else{
printf("Yes\n");
double t1,t2,t3;
if(r1>r2) t1=r1;
else t1=r2;
if(t1