【十大经典数据挖掘算法】系列
- C4.5
- K-Means
- SVM
- Apriori
- EM
- PageRank
- AdaBoost
- kNN
- Naïve Bayes
- CART
1. 前言
分类与回归树(Classification and Regression Trees, CART)是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出,既可用于分类也可用于回归。本文将主要介绍用于分类的CART。CART被称为数据挖掘领域内里程碑式的算法。
不同于C4.5,CART本质是对特征空间进行二元划分(即CART生成的决策树是一棵二叉树),并能够对标量属性(nominal attribute)与连续属性(continuous attribute)进行分裂。
2. CART生成
前一篇提到过决策树生成涉及到两个问题:如何选择最优特征属性进行分裂,以及停止分裂的条件是什么。
特征选择
CART对特征属性进行二元分裂。特别地,当特征属性为标量或连续时,可选择如下方式分裂:
An instance goes left if CONDITION, and goes right otherwise
即样本记录满足CONDITION则分裂给左子树,否则则分裂给右子树。
标量属性
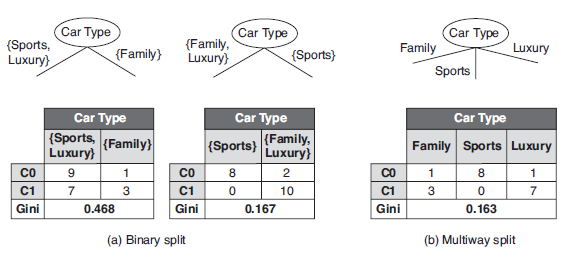
进行分裂的CONDITION可置为不等于属性的某值;比如,标量属性Car Type取值空间为{Sports, Family, Luxury},二元分裂与多路分裂如下:
连续属性
CONDITION可置为不大于\(\varepsilon\);比如,连续属性Annual Income,\(\varepsilon\)取属性相邻值的平均值,其二元分裂结果如下:
接下来,需要解决的问题:应该选择哪种特征属性及定义CONDITION,才能分类效果比较好。CART采用Gini指数来度量分裂时的不纯度,之所以采用Gini指数,是因为较于熵而言其计算速度更快一些。对决策树的节点\(t\),Gini指数计算公式如下:
\begin{equation}
Gini(t)=1-\sum\limits_{k}[p(c_k|t)]^2
\end{equation}
Gini指数即为\(1\)与类别\(c_k\)的概率平方之和的差值,反映了样本集合的不确定性程度。Gini指数越大,样本集合的不确定性程度越高。分类学习过程的本质是样本不确定性程度的减少(即熵减过程),故应选择最小Gini指数的特征分裂。父节点对应的样本集合为\(D\),CART选择特征\(A\)分裂为两个子节点,对应集合为\(D_L\)与\(D_R\);分裂后的Gini指数定义如下:
\begin{equation}
G(D,A)={\left|{D_L} \right| \over \left|{D} \right|}Gini(D_L)+{\left|{D_R} \right| \over \left|{D} \right|}Gini(D_R)
\end{equation}
其中,\(\left| \cdot \right|\)表示样本集合的记录数量。如上图中的表格所示,当Annual Income的分裂值取87时,则Gini指数计算如下:
\[ \frac{4}{10} \left[ 1- (\frac{1}{4})^2- (\frac{3}{4})^2 \right] + \frac{6}{10} \left[ 1- (\frac{2}{6})^2- (\frac{4}{6})^2 \right] = 0.417 \]
CART算法
CART算法流程与C4.5算法相类似:
- 若满足停止分裂条件(样本个数小于预定阈值,或Gini指数小于预定阈值(样本基本属于同一类,或没有特征可供分裂),则停止分裂;
- 否则,选择最小Gini指数进行分裂;
- 递归执行1-2步骤,直至停止分裂。
3. CART剪枝
CART剪枝与C4.5的剪枝策略相似,均以极小化整体损失函数实现。同理,定义决策树\(T\)的损失函数为:
\begin{equation}
L_\alpha (T)=C(T)+\alpha \left| T \right|
\end{equation}
其中,\(C(T)\)表示决策树的训练误差,\(\alpha\)为调节参数,\(\left| T \right|\)为模型的复杂度。
CART算法采用递归的方法进行剪枝,具体办法:
- 将\(\alpha\)递增\(0={\alpha}_0<{\alpha}_1<{\alpha}_2<\cdots<{\alpha}_n\),计算得到对应于区间\([\alpha_{i},{\alpha}_{i+1})\)的最优子树为\(T_i\);
- 从最优子树序列\(\lbrace T_1,T_2,\cdots,T_n \rbrace\)选出最优的(即损失函数最小的)。
如何计算最优子树为\(T_i\)呢?首先,定义以\(t\)为单节点的损失函数为
\[ L_\alpha (t)=C(t)+\alpha \]
以\(t\)为根节点的子树\(T_t\)的损失函数为
\[ L_\alpha (T_t)=C(T_t)+\alpha \left| T_t \right| \]
令\(L_\alpha (t)=L_\alpha (T_t)\),则得到
\[ \alpha = {C(t)-C(T_t) \over \left| T_t \right|-1} \]
此时,单节点\(t\)与子树\(T_t\)有相同的损失函数,而单节点\(t\)的模型复杂度更小,故更为可取;同时也说明对节点\(t\)的剪枝为有效剪枝。由此,定义对节点\(t\)的剪枝后整体损失函数减少程度为
\[ g(t) = {C(t)-C(T_t) \over \left| T_t \right|-1} \]
剪枝流程如下:
- 对输入决策树\(T_0\),自上而下计算内部节点的\(g(t)\);选择最小的\(g(t)\)作为\({\alpha}_1\),并进行剪枝得到树\(T_1\),其为区间\([{\alpha}_1,{\alpha}_2)\)对应的最优子树。
- 对树\(T_1\),再次自上而下计算内部节点的\(g(t)\);……\(\alpha _2\)……\(T_2\)……
- 如此递归地得到最优子树序列,采用交叉验证选取最优子树。
关于CART剪枝算法的具体描述请参看[1],其中关于剪枝算法的描述有误:
(6)如果T不是由根节点单独构成的树,则回到步骤(4)
应改为回到步骤(3),要不然所有\(\alpha\)均一样了。
-----------------------------------------------Update ------------------------------------------------------
李航老师已经在勘误表给出修改了。
4. 参考资料
[1] 李航,《统计学习方法》.
[2] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
[3] Dan Steinberg, The Top Ten Algorithms in Data Mining.