目录
- 分组卷积
- 深度可分离卷积
- 倒残差模块和线性瓶颈模块
- 激活函数
- 通道混合
- FLOPs不等同于Speed
- 参考
分组卷积
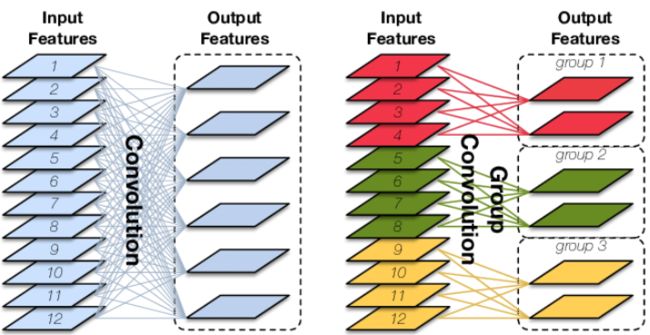
分组卷积(Group Convolution)最早见于AlexNet以切分网络,是一种降低参数量和计算量的方法,是模型轻量化的一种基础方法。
分组卷积就是对输入的特征图进行分组,然后分别进行卷积,然后将结果堆积起来。设输入特征图为\(D_{in}\times H\times W\),输出特征图维度为\(D_{out}\),常规卷积核的参数量为\(K^2D_{in}D_{out}\);在分组卷积中,设分组数量为\(G\),那么每组输出的特征图维度为\(\frac{D_{out}}{G}\),每个卷积核参数量为\(K^2\frac{D_{in}}{G}\frac{D_{out}}{G}\),\(G\)个卷积的总参数量为\(K^2D_{in}D_{out}\frac{1}{G}\),为常规卷积的\(\frac{1}{G}\)。
分组卷积的思想被广泛地运用在网络设计中,除了可以降低参数量,还可以被视为一种结构化稀疏方法,相当于一种正则化方法。
当分组数与特征图输入输出维度相等时,即\(G=D_{in}=D_{out}\),相当于MobileNet和Xception中的深度卷积(Depthwise Convolution)。
当分组数与特征图输入输出维度相等时,即\(G=D_{in}=D_{out}\),且当卷积核的输入尺度与输入特征图维度时,即\(K=W=H\),输入的特征图为\(C\times 1\times 1\),在MobileFaceNet中称之为Global Depthwise Convolution(GDC),即全局加权池化,与Global Average Pooling(GAP)不同,GDC给每个位置赋予了可学习的权重(对于已对齐的图像这很有效,比如人脸,中心位置和边界位置的权重自然应该不同)。
深度可分离卷积
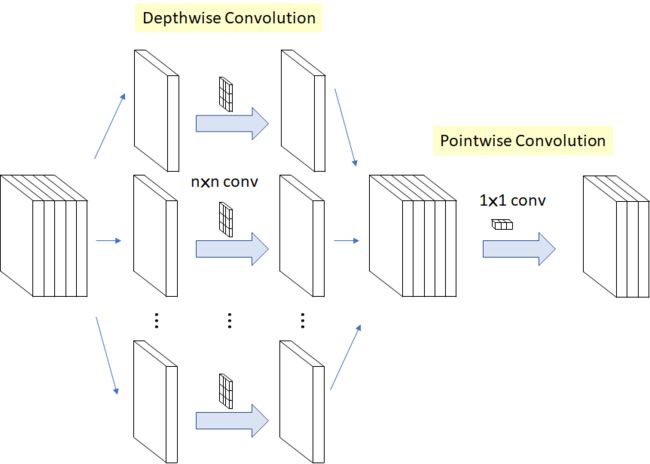
深度可分离卷积分为深度卷积和逐点卷积两部分,即SeparableConv由DepthWiseConv和PointWiseConv组成,是降低卷积运算参数量的一种有效方法。
在Google的Xception以及MobileNet论文中均有描述。它的核心思想是将一个完整的卷积运算分解为两步进行,分别为Depthwise Convolution与Pointwise Convolution。
Pytorch代码为:
from torch import nn
class SeparableConv2d(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size=1, stride=1, padding=0, onnx_compatible=False):
super().__init__()
ReLU = nn.ReLU if onnx_compatible else nn.ReLU6
self.conv = nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=in_channels, kernel_size=kernel_size,
groups=in_channels, stride=stride, padding=padding),
nn.BatchNorm2d(in_channels),
ReLU(),
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1),
)
def forward(self, x):
return self.conv(x)设特征图的输入层数为\(D_{in}\),输出层数为\(D_{out}\),卷积核的尺度为\(K\times K\)。
深度可分离卷积的参数量为\(K^2D_{in} + D_{in}D_{out}\),常规卷积的参数量为\(K^2D_{in}D_{out}\),两者比例为 \(\frac{1}{D_{out}}+\frac{1}{K^2}\),因此可以减少参数量和计算量。
同时注意到采用了\(\rm{ReLU6}\)的激活函数,实际上\(\rm{ReLU6}(x)=\min(\max(0, x), 6)\),即给\(\rm{ReLU}\)激活函数添加一个上届。作者认为\(\rm{ReLU6}\)在低精度计算下更加鲁棒。
倒残差模块和线性瓶颈模块
倒残差模块(Inverted Residuals)和(Linear Bottlenck)由MobileNetV2提出,用来解决MobileNet中Depthwise部分卷积核容易废掉的问题。
出发点可以参考知乎,简单讲就是当低维信息映射到高维,经过ReLU后再映射回低维时,若映射到的维度相对较高,则信息变换回去的损失较小;若映射到的维度相对较低,则信息变换回去后损失很大。
图中Input的的螺旋线数据记为\(X_m\),\(m=2\)表示二维数据,生成随机矩阵\(T\)将\(X_m\)映射到\(n\)维上,通过激活函数\(ReLU\)在使用\(T^{-1}\)映射回2维空间,
即\(X'_m=T^{-1}\mathrm{ReLU}(TX_m)\),根据n的不同取值可以图:

说明对低维数据做\(\mathrm{ReLU}\)容易造成信息的丢失,MobileNetV2设计了两个模块解决这个问题。
最直接的方法就是将MobileNet模块中的最后的一个\(\mathrm{ReLU6}\)该为线性激活函数。
此外,DepthWise卷积本身并不能改变通道数量,因此可以在DW之前进行PW扩张通道数量,然后在高维度数据上进行DW,扩张因子选择了6,即是6倍的扩张。
这样一来就与残差模块中的设计不同,残差网络通过1x1卷积进行维度压缩(因子0.25),因此这种设计被称为倒残差模块。
两者组合起来就是MobileNetV2中的模块,当stride为2时,由于输入和输出特征图的尺度不同,就没有了shortcut,如图所示:
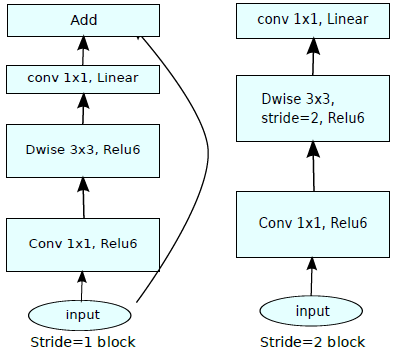
pytorch代码为:
class InvertedResidual(nn.Module):
def __init__(self, inp, oup, stride, expand_ratio):
super(InvertedResidual, self).__init__()
self.stride = stride
assert stride in [1, 2]
hidden_dim = int(round(inp * expand_ratio))
self.use_res_connect = self.stride == 1 and inp == oup
layers = []
if expand_ratio != 1:
# pw
layers.append(ConvBNReLU(inp, hidden_dim, kernel_size=1))
layers.extend([
# dw
ConvBNReLU(hidden_dim, hidden_dim, stride=stride, groups=hidden_dim),
# pw-linear
nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
nn.BatchNorm2d(oup),
])
self.conv = nn.Sequential(*layers)
def forward(self, x):
if self.use_res_connect:
return x + self.conv(x)
else:
return self.conv(x)激活函数
在嵌入式设备上执行sigmoid函数需要耗费相当大的计算资源,使用一种计算量小的函数去逼近它,让它变硬(hard),可以有效降低计算消耗。
作者使用了ReLU6对其进行逼近,得到了
\[\rm{h-sigmoid} = \frac{\rm{ReLU6}(x+3)}{6}\]
类似的,swish函数具备无上届有下界、平滑、非单调的特性,并且在深层模型上的效果优于ReLU,作者使用ReLU6对其逼近,得到了h-swish激活函数。
\[\rm{h-swish} = x\frac{\rm{ReLU6}(x+3)}{6}\]
作者认为由于特征图尺度随着网络的加深而减少,非线性激活函数的成本也会随之减少,因此仅在网络的后半段使用h-swish代替了ReLU6,并使用h-sigmoid代替了sigmoid。
尽管使用h-swish会带来一定量的延迟,但是在使用优化实现的h-swish可以一定量的降低延迟。
通道混合
分组卷积的一个问题是不同组之间的特征图需要通信,不然会降低网络的提取能力,因此在Xception和MobileNet中密集采用PW(1x1卷积)以保证不同特征图的通信,这也导致了mobilenet 中1x1卷积占据了绝大部分的计算资源。
shufflenet提出了一种低计算复杂度的方法以保证不同组特征间的通信,如下图(c)所示,对DW之后的特征进行混合(均匀打乱),在pytorch中仅通过维度和转置操作即可以完成。
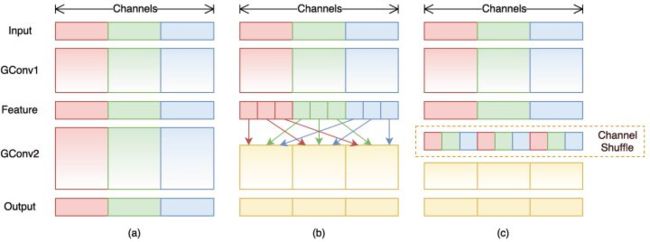
相应的pytorch代码为:
class ShuffleBlock(nn.Module):
def __init__(self, groups):
super(ShuffleBlock, self).__init__()
self.groups = groups
def forward(self, x):
"""Channel shuffle: [N, C, H, W] -> [N, g, C/g, H, W] -> [N, c/g, g, H, W] -> [N, C, H, W]"""
N, C, H, W = x.size()
g = self.groups
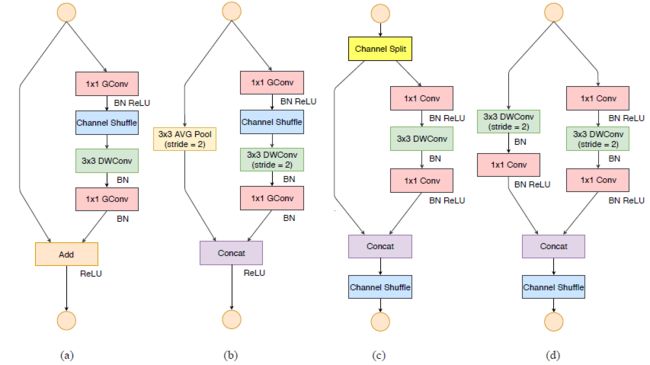
return x.view(N, g, C / g, H, W).permute(0, 2, 1, 3, 4).contiguous().view(N, C, H, W)如下图所示,shufflenet中基本单元是从残差单元改进而来,其中图(a)是残差单元,图(b)和(c)分别是stride为1和2时的shufflenet基本单元。注意到在DW卷积之后没有激活函数,1x1卷积采用了分组的形式,此外当stride=2中的shortcut采用了平均池化,和concat操作以降低运算量。
相应的pytorch代码为:
class Bottleneck(nn.Module):
def __init__(self, in_planes, out_planes, stride, groups):
super(Bottleneck, self).__init__()
self.stride = stride
mid_planes = out_planes / 4
g = 1 if in_planes == 24 else groups
self.conv1 = nn.Conv2d(in_planes, mid_planes, kernel_size=1, groups=g, bias=False)
self.bn1 = nn.BatchNorm2d(mid_planes)
self.shuffle1 = ShuffleBlock(groups=g)
self.conv2 = nn.Conv2d(mid_planes, mid_planes, kernel_size=3, stride=stride,
padding=1, groups=mid_planes, bias=False)
self.bn2 = nn.BatchNorm2d(mid_planes)
self.conv3 = nn.Conv2d(mid_planes, out_planes, kernel_size=1, groups=groups, bias=False)
self.bn3 = nn.BatchNorm2d(out_planes)
self.shortcut = nn.Sequential() if stride == 2\
else nn.Sequential(nn.AvgPool2d(3, stride=2, padding=1))
self.relu = nn.ReLU(True)
def forward(self, x):
out = self.relu(self.bn1(self.conv1(x)))
out = self.shuffle1(out)
out = self.bn2(self.conv2(out))
out = self.bn3(self.conv3(out))
res = self.shortcut(x)
out = self.relu(torch.cat((out, res), 1)) if self.stride == 2 else self.relu(out + res)
return outFLOPs不等同于Speed
FLOPS(floating point of per seconds)是每秒浮点运算次数,用来衡量硬件的性能。
FLOPs(floating point of operations)是浮点运算次数,可以用来衡量算法/模型的复杂度。
在轻量级网络设计中,FLOPs经常被用来衡量网络的速度,然而在ShuffleNetV2中提到,FLOPs并不直接等于网络的执行速度,主要原因有:
- 内存访问的成本(MAC)
- 模型计算的并行程度
- CuDNN对3x3卷积有特殊优化,因此1x1卷积的速度不可能9倍的快于3x3
基于以上原因,作者在使用直接指标(计算速度,即每秒batch数量)代替了间接指标(FLOPs),并在目标硬件平台(GPU和ARM)上进行了实验,得到了四条实践原则:
- 相同的通道宽度可以最小化内存访问成本(MAC);
- 过量分组卷积增加MAC;
- 网络碎片(多路径结构)降低并行程度;
- 元素级操作(Add, ReLU等)不可忽视
在以上四条指导原则的基础上,作者对ShuffleNetV1的基本单元进行了改进。
如下图所示,其中(a)和(b)分别是shuffleNetV1的stride=1和2基本单元,(c)和(d)分别是shuffleNetV2的stride=1和2基本单元。
对于stried=1的基本单元,具体的改进步骤:
- 使用channel split 对输入特征图进行二分离,这一步相当于分组;
- 在G3的原则下,对左分支保持不变,仅右分支进行操作;
- 在G1的原则下,对右分支的操作进行三次卷积操作;
- 在G2的原则下,1x1卷积中的分组取消,第一个1x1卷积后的channel shuffle也随之取消;
- 在G1的原则下,保持输出特征图不变,使用channel contact操作将左右分支合并,然后进行channel shuffle保证分组之后的通信。
这里有一个很有意思的地方,分组卷积是轻量级网络设计的一种常用方法,但是过量的分组会增大MAC,使用channel split, shuffle, 和contact也可以实现分组与通信,且使用仅对split的一侧分支进行操作,也符合G4的原则。
对应的pytorch代码为:
import torch
from torch import nn
class MyShuffleV2Unit(nn.Module):
def __init__(self, in_channels, out_channels, stride=1, splits_left=2, groups=2):
super(MyShuffleV2Unit, self).__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.stride = stride
self.splits_left = splits_left
self.groups = groups
if stride == 2:
self.right_in_channels, self.right_out_channels = in_channels, out_channels // 2
else:
self.right_in_channels = in_channels - in_channels // splits_left
self.right_out_channels = self.right_in_channels
self.left = None if stride == 1 else \
nn.Sequential(*[
nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=2,
padding=1, bias=True, groups=in_channels),
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels // 2, kernel_size=1, stride=1, padding=0, bias=True),
nn.BatchNorm2d(out_channels // 2),
nn.ReLU(True)
])
self.right = nn.Sequential(*[
nn.Conv2d(self.right_in_channels, self.right_in_channels, 1, 1, 0, True),
nn.BatchNorm2d(self.right_in_channels),
nn.ReLU(True),
nn.Conv2d(self.right_in_channels, self.right_in_channels, 3,
stride, 1, True, groups=self.right_in_channels),
nn.BatchNorm2d(self.right_in_channels),
nn.Conv2d(self.right_in_channels, self.right_out_channels, 1, 1, 0, True),
nn.BatchNorm2d(self.right_out_channels),
nn.ReLU(True)
])
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_uniform_(m.weight)
if m.bias is not None:
nn.init.constant_(m.bias, 0)
def forward(self, x):
if self.stride == 2:
x_left, x_right = x, x
x_left, x_right = self.left(x_left), self.right(x_right)
else:
x_left, x_right = torch.split(x, [self.in_channels // self.splits_left,
self.in_channels // self.splits_left], dim=1)
x_right = self.right(x_right)
x = torch.cat([x_left, x_right], dim=1)
# channel_shuffle
N, C, H, W = x.size()
g = self.groups
x = x.view(N, g, C // g, H, W).permute(0, 2, 1, 3, 4).contiguous().view(N, C, H, W)
return x
参考
https://www.cnblogs.com/shine-lee/p/10243114.html
https://www.cnblogs.com/dengshunge/p/11334640.html
https://zhuanlan.zhihu.com/p/32304419
https://zhuanlan.zhihu.com/p/70703846
https://github.com/lufficc/SSD
https://github.com/Marcovaldong/LightModels