【Network】优化问题——Label Smoothing

滴：转载引用请注明哦【握爪】https://www.cnblogs.com/zyrb/p/9699168.html 

　　今天来进行讨论深度学习中的一种优化方法Label smoothing Regularization(LSR)，即“标签平滑归一化”。由名字可以知道，它的优化对象是Label(Train_y)。

　　对于分类问题，尤其是多类别分类问题中，常常把类别向量做成one-hot vector(独热向量)。

简单地说，就是对于多分类向量，计算机中往往用[0, 1, 3]等此类离散的、随机的而非有序(连续)的向量表示，而one-hot vector 对应的向量便可表示为[0, 1, 0]，即对于长度为n 的数组，只有一个元素是1，其余都为0。

之后在网络的最后一层（全连接层）后加一层softmax层，由于softmax输出是归一化的，所以认为该层的输出就是样本属于某类别的概率。而由于样本label是独热向量，因此表征我们已知样本属于某一类别的概率是为1的确定事件，属于其他类别的概率则均为0。

　　【一】、首先明确一些变量的含义：

$z_i$：也为logits，即未被归一化的对数概率；

$p$：predicted probability，预测的example的概率；

$q$：groundtruth probablity，真实的example的label概率；对于one-hot，真实概率为Dirac函数，即$​q(k)=δ_{k,y}$，其中y是真实类别。

$loss$：Cross Entropy，采用交叉熵损失。

softmax层的输出预测概率为：\begin{equation} p(k|x)=\frac{exp(z_k)}{\sum_{i}^{i=K}exp(z_i)} \end{equation}

交叉熵损失表示为：​\begin{equation}loss=−\sum_{k=1}^{K}q(k|x)log(p(k|x)) \end{equation}

对于logits，交叉熵是可微分的，偏导数的形式也较为简单：$\frac{∂loss}{∂zk}=p(k)−q(k)$(对于$p,q ∈[0, 1]$, 可以知道梯度是有界的∈[-1, 1])

　　【二】、one-hot 带来的问题

　　对于损失函数，我们需要用预测概率去拟合真实概率，而拟合one-hot的真实概率函数会带来两个问题：1)无法保证模型的泛化能力，容易造成过拟合；2) 全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大，而由梯度有界可知，这种情况很难adapt。会造成模型过于相信预测的类别。

　　【三】、解决方案

　　为了使得模型less confident，提出以下机制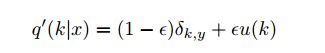：,将$q(k)$函数改为$q(k)'$。

 {原理解释}：对于以Dirac函数分布的真实标签，我们将它变成分为两部分获得（替换）

1) 第一部分：将原本Dirac分布的标签变量替换为(1 - ϵ)的Dirac函数；

2) 第二部分：以概率 ϵ ，在$u(k)$ 中份分布的随机变量。（在文章中，作者采用先验概率也就是均布概率，而K取值为num_class = 1000）

　　从而交叉熵被替换为：

可以认为：Loss 函数为分别对【预测label与真实label】【预测label与先验分布】进行惩罚。

　　【四】、优化结果

　　文章表示，对K = 1000，ϵ = 0.1的优化参数，实验结果有0.2%的性能提升。

 

Reference：

1. Rethinking the Inception Architecture for Computer Vision

2. 深度学习中的各种tricks_1.0_label_smoothing