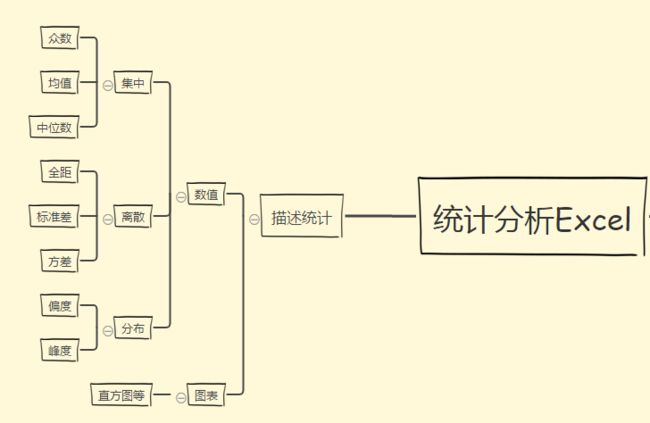
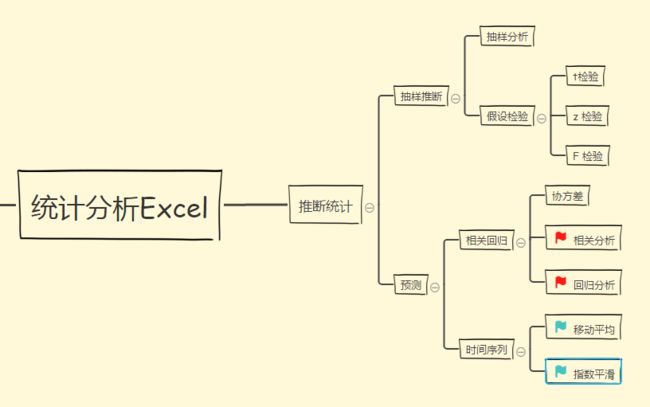
Analysis Toolpak 是EXCEL的数据分析工具包,可以代替SPSS做简单的方差分析、相关回归、t检验、F检验,还有基础的描述统计、抽样、随机...
1. 首先,你得在EXCEL加载项中添加数据分析工具包:
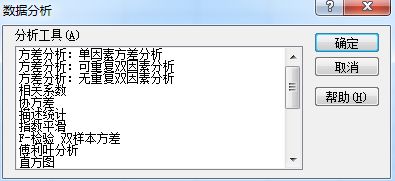
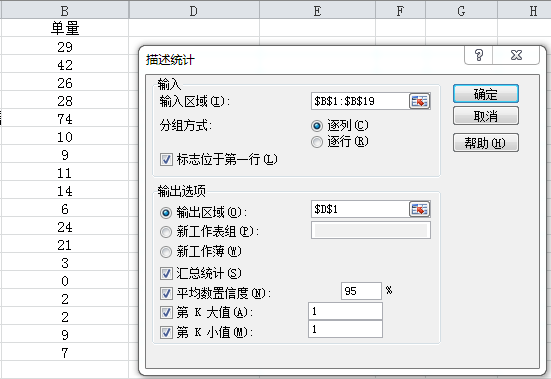
2. 从描述统计开始尝试:
☆ 分组方式:选择原始数据中每个变量是按行排列还是按列排列
☆ 标志位于第一行:选中数据区域中是否包含变量名
☆ 汇总统计:输出所有常用的描述统计指标
☆ 平均数置信度:置信区间,通常α是.05,CI选择95%
☆ 第K大/小值:输出你关心的排名对应的数值
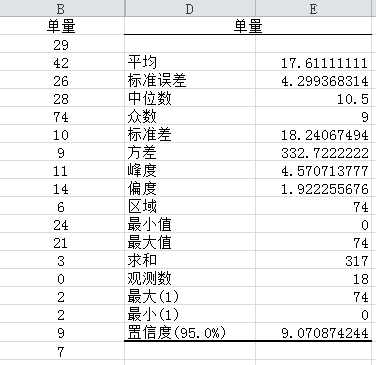
可以看到选中数据集的集中、离散、分布(相对于正态)参数,样本量、和、置信区间
复习一下峰度、偏度以及置信区间的概念:
峰度>0,分布图比正态分布图更高更瘦,数据更集中
峰度<0,分布图比正态分布图更矮更胖,数据峰分散
偏度>0,正偏态分布,最高值往左移动,长尾向右
偏度<0,负偏态分布,最高值往右移动,长尾向左
95%置信区间:抽样样本对应的【总体的均值】落在该区间内的概率为95%
根据图中给出的置信度,可以得出95%置信区间为 [17.61-9.07,17.61+9.07 ]
图中给出的是围绕样本均值给出的区间的长度的一半,在这个区间内有95%可能捕捉到总体均值
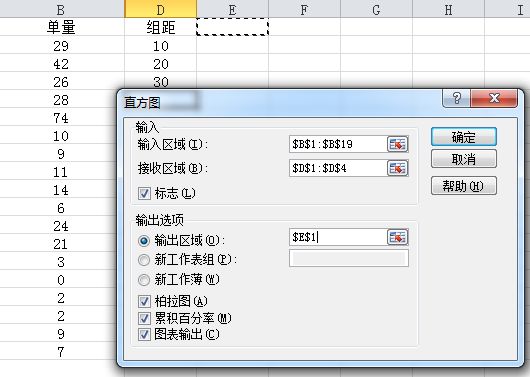
3. 再画个直方图:
☆ 首先要定义一下分组的组距(EXCEL只能画数值分组的频率直方图)
☆ 如果选中区域包含变量名,一定要勾选【标志】
☆ 一定要勾选【图表输出】
☆ 如果需要在直方图上加一条累计百分比的折线,勾选【累计百分率】
☆ 如果需要把横坐标按照频率高低重新排布,勾选【柏拉图】
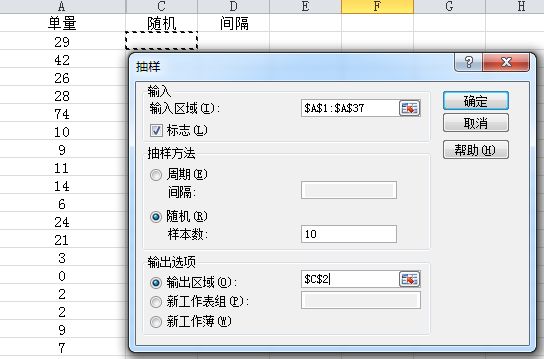
4. 抽样
抽样的第一步是从总体中随机/按照一定规律抽取样本,第二步是对样本进行假设检验来推论总体参数,包括t检验(2样本均值)、z检验(2样本均值查)、F检验(2样本方差)
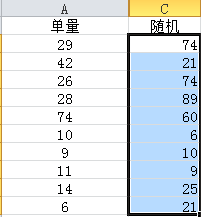
EXCEL的抽样是【有放回抽样】,所以一个Case可能被抽到多次,如果你不希望重复,可以多次抽样,然后得到一个不重复的样本
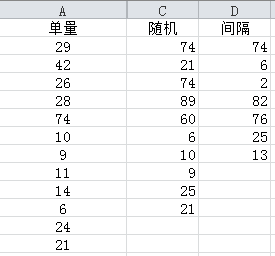
周期抽样得到的样本是由样本量和间隔决定的(一共36个样本,间隔为5,只能得到7个Case)
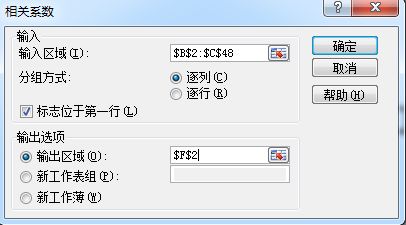
5. 来个相关分析
相关分析:研究2个或以上随机变量之间相互依存关系的方向和密切程度
直线相关-相关系数 (绝对值在0.3-0.8之间算中度相关,it depends)
曲线相关-相关指数
多重相关-复相关系数
6. 如果相关很强,可以考虑一下回归
相关VS.回归
相关是没有方向的,都是随机变量;回归有方向,自变量是确定变量,因变量是随机变量
相关能得到相关系数,回归可以得到回归系数
相关只能根据正负相关判断依存变化方向,回归能通过自变量去预测因变量的变化方向和程度
第一步,确定自变量因变量:用推广费用预测销售额
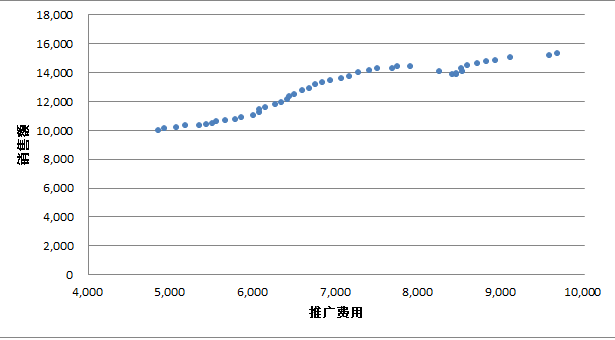
第二步, 绘制散点图
A 选中横坐标轴,重新设定坐标轴最大值最小值以及间隔值
B 更改图标呈现方式,呈现并更改坐标轴标题,删除表名和系列标识
C 选中散点序列,右键更改格式,调整形状和大小,使图表清晰
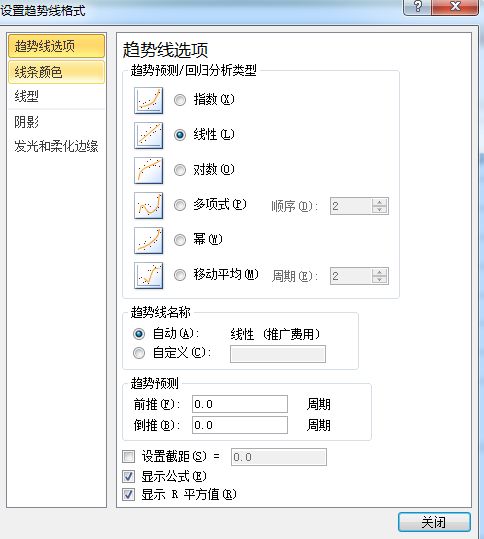
第三步,求参数,搭模型
A 在类别中选中【线性】
B 勾选【显示公式】
C 勾选【显示R平方值】
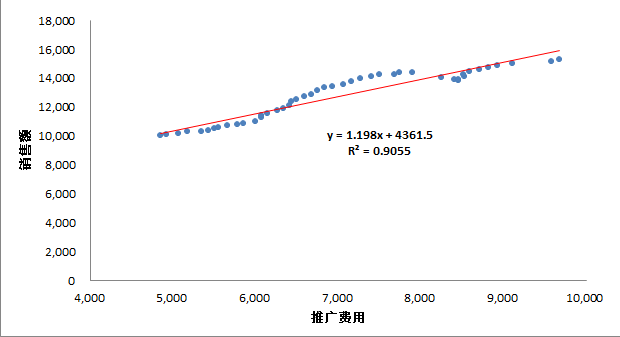
方程和R方都如图所示:
第四步,进行3个检验
输入:选择XY来源,确定是否包含变量名(标志),确认CI概率,常数为0就是正比例函数
残差:预测值与观测值之间的差值——勾选残差、标准残差,会输出对应的数值
残差图:IV为横轴,残差为纵轴——若点在X=0上下随机分布,则拟合合理,反之重新建模
线性拟合图:IV为横轴,DV+DV-expected为纵轴——对比预测值与真实值的分布
正态概率图:IV百分位排名为横轴,DV为纵轴——若为直线则符合正态分布
A 回归统计表——>拟合优度检验(R方)——回归模式是否很好拟合这些数据?
Multiple R——>相关系数绝对值
R Square——>R方,判定系数
Adjusted——>在多重回归中,衡量加入新的自变量后模型的拟合程度是否变好
Std.Error of the Estimate(翻译有误)——>残差的标准差/剩余标准差,越小拟合程度越好
B 方差分析表——>回归模型的显著性检验(F test)——线性回归模型能否描述变量间关系?
——因变量与所有自变量间的线性关系是否显著?
Df ——>自由度
SS ——>误差平方和
MS ——>均方差
F ——> F统计量,报告的时候需要报告F值和对应p值
Sig F——> 此处代表p值(命名有歧义),即当H0成立时出现当前F值的概率,如果p<α=.05/.01,则推翻H0,认为模型显著
C 回归系数表——>回归系数的显著性检验(t test)——指定的线性回归模型是否显著?
——因变量与每一个自变量间的线性关系是否显著?
Intercept——>截距
Coefficient——>回归系数的值
各自变量对应行表示该自变量与因变量之间线性关系的检验结果:
若p<α&系数落入95%置信区间,表示该自变量与因变量间的线性关系显著,报告t值+对应的p值
综合上述3个表格的结果给出关于回归模型拟合效果的结论:
回归模型为...其中判定系数为...回归模型拟合效果较好,回归模型的F检验与回归系数的t检验对应的p值都远小于.01,具有显著线性关系。综合来说,回归模型拟合较好。
第五步,根据给出的X值,用回归模型预测Y值
☆ 多重线性回归
步骤一律同上,结果解读和报告要选择 Adjusted R Square!
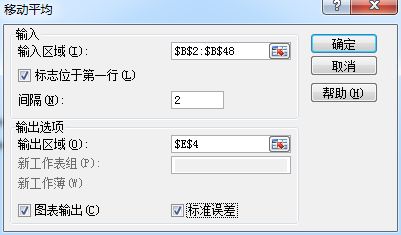
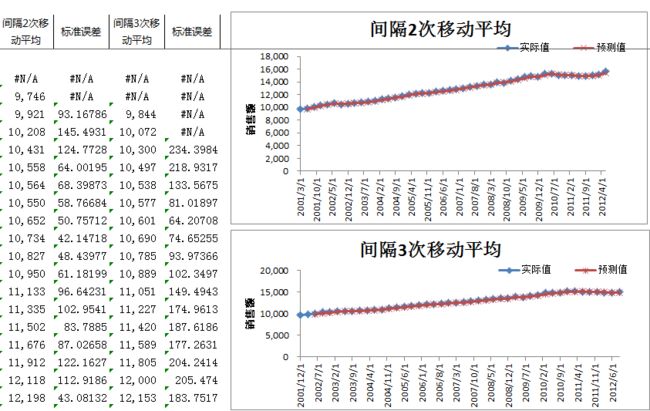
7. 时间序列预测——>移动平均——>用算数平均值作为预测值
间隔为N就是指——取最后N个值求平均值
此处的预测值就是——把往前N个实际值得算数平均值(其他的数据都没有被利用)
间隔2次第一个日期无对应的预测值,间隔3次前2个日期无对应的预测值
把新生成的4个列下拉得到对应值,保留标准误差小的预测值
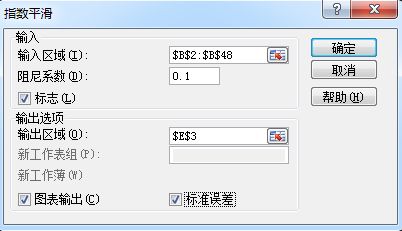
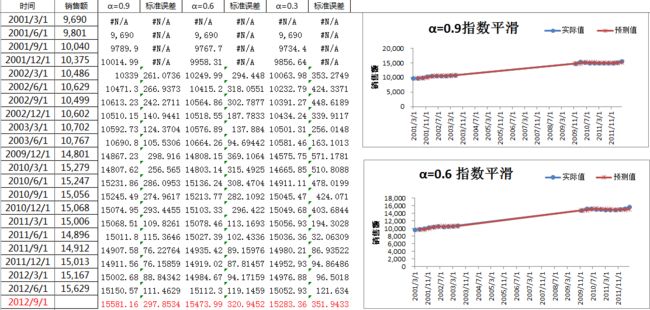
8. 时间序列预测——>指数平滑——>用加权平均值作为预测值
α——平滑系数,取值0-1
β——阻尼系数,取值0-1
β=1-α,所以你只需要设定β
β怎么设定:如果你手头的数据集随时间波动不大,令β=0.1/0.2/0.3 各试一遍选最优
如果波动大,令β=0.7/0.8/0.9 各试一遍选最优 (实际上你想从0.1-1.0都试一遍也成)
把新生成的各列下拉得到对应值,保留标准误差最小的预测值:本例选择α=.9时的预测值
——————————图表如果不清晰,可以单击以查看原图
Done Bravo~