大数据分析常用去重算法分析『HyperLogLog 篇』

在上篇推送中，Kyligence 大数据工程师陶加涛为大家介绍了利用 Roaring Bitmap 来进行精确去重。虽然这种算法能大大地减少存储开销，但是随着数据量的增大，它依然面临着存储上的压力。在本篇推送中将要介绍的 HyperLogLog （下称 HLL） 是一种非精确的去重算法，它的特点是具有非常优异的空间复杂度（几乎可以达到常数级别）。

HLL 算法需要完整遍历所有元素一次，而非多次或采样；该算法只能计算集合中有多少个不重复的元素，不能给出每个元素的出现次数或是判断一个元素是否之前出现过；多个使用 HLL 统计出的基数值可以融合。

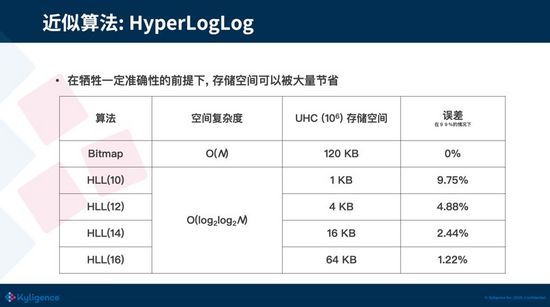
HLL 算法有着非常优异的空间复杂度，可以看到它的空间占用随着基数值的增长并没有变化。 HLL 后面不同的数字 代表着不同的精度，数字越大，精度越高，占用的空间也越大，可以认为 HLL 的空间占用只和精度成正相关。

HLL算法原理感性认知

HLL 算法的原理会涉及到比较多的数学知识，这边对这些数学原理和证明不会展开。举一个生活中的例子来帮助大家理解HLL算法的原理：比如你在进行一个实验，内容是不停地抛硬币，记录你连续抛到正面的次数（这是数学中的伯努利过程，感兴趣同学可以自行研究下）；如果你最多的连抛正面记录是3次，那可以想象你并没有做这个实验太多次，如果你最长的连抛正面记录是 20 次，那你可能进行了这个实验上千次。

一种理论上存在的情况是，你非常幸运，第一次进行这个实验就连抛了 20 次正面，我们也会认为你进行了很多次这个实验才得到了这个记录，这就会导致错误的预估；改进的方式是请 10 位同学进行这项实验，这样就可以观察到更多的样本数据，降低出现上述情况的概率。这就是 HLL 算法的核心思想。

HLL算法具体实现

HLL 会通过一个 hash 函数来求出集合中所有元素的 hash 值（二进制表示的 hash 值，就可以理解为一串抛硬币正反面结果的序列），得到一个 hash 值的集合，然后找出该 hash 值集合中，第一个 1 出现的最晚的位置。例如有集合为 [010, 100, 001], 集合中元素的第一个 1 出现的位置分别为 2, 1, 3，可以得到里面最大的值为 3，故该集合中第一个1出现的最晚的位置为 3。因为每个位置上出现1的概率都是 1/2，所以我们可以做一个简单的推断，该集合中有 8 个不重复的元素。

可以看到这种简单的推断计算出来集合的基数值是有较大的偏差的，那如何来减少偏差呢？ 正如我上面的例子里说的一样，HLL 通过多次的进行试验来减少误差。 那它是如何进行多次的实验的呢？这里 HLL  使用了分桶的思想 ，上文中我们一直有提到一个精度的概念，比如说 HLL(10)，这个 10 代表的就是取该元素对应 Hash 值二进制的后 10 位，计算出记录对应的桶，桶中会记录一个数字，代表对应到该桶的 hash 值的第一个 1 出现的最晚的位置。如上图，该 hash 值的后 10 位的 hash 值是 0000001001，转成 10 进制是 9，对应第 9 号桶，而该 hash 值第一个 1 出现的位置是第 6 位，比原先 9 号桶中的数字大，故把 9 号桶中的数字更新为 6。 可以看到桶的个数越多，HLL 算法的精度就越高 ，HLL(10) 有 1024( 2 10 ) 个桶，HLL(16)有 65536( 2 16 ) 个桶。同样的，桶的个数越多，所占用的空间也会越大。

刚才的例子我们省略了一些细节，为了让大家不至于迷失在细节中而忽视了重点，真实的 HLL 算法的完整描述见上图，这边的重点是 计算桶中平均数时使用调和平均数 。调和平均数的优点是可以过滤掉不健康的统计值，使用算术平均值容易受到极值的影响（想想你和马云的平均工资），而调和平均数的结果会倾向于集合中比较小的元素。HLL 论文中还有更多的细节和参数，这边就不一一细举，感兴趣的同学可以自己阅读下论文。

HLL评估

HLL 的误差分布服从正态分布，它的空间复杂度: O(m log 2 log 2 N) , Ｎ 为基数, m 为桶个数。这边给大家推导一下它的空间复杂度，我有 2 6 4 个的不重复元素(Long. MAX_VALUE)，表达为二进制一个数是 64 位，这是第一重 log 2 , 那么第一个1最晚可能出现在第 64 位。64 需要 6 个 bit ( 2 6=64) 就可以存储，这是第二重   log 2 。如果精度为 10，则会有 1024 个桶，所以最外面还要乘以桶的个数。由于需要完整的遍历元素一遍，所以它的时间复杂度是一个线性的时间复杂度。

在Kylin中的应用

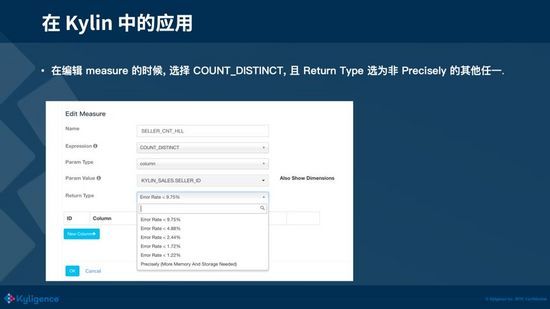
在 Kylin 中使用 HLL 非常简单，在编辑度量的页面选择 COUNT DISTINCT，Return Type 选为非 Precisely 的其他选项，大家根据自己的需求选择不同的精度就可以愉快地使用了。

我们回到最开始的去重场景，看看使用了 Bitmap 和 HLL 会给我们带来什么增益：无优化 case 下，每个 item 对应的 user_id 就可以看成 存储原始值的一个集合 ；在使用 Bitmap 优化的case 下，每个 item 对应的 user_id 就可以看成一个 Bitmap 实例，同理 HLL就是一个 HLL 的实例， Bitmap/HLL 实例占用的空间都会比直接存储原始值的集合要小，这就达到了我们开始提的减少 shuffle 数据量的需求。

Q：您好，问一下关于精确去重的问题， 我选择了非精确去重，最后的误差率有时候会比界面上提示的值要高一些，这是为什么？

A：首先 HLL 的误差分布服从正态分布，也就是说是在99%的情况下是这个误差，同时 HLL 对于基数比较低的情况，误差会偏高。如果你的基数比较低的话，我推荐使用精确去重。

Q：我想要了解一下 Bitmap 在 Kylin 中，它最终落盘在 HBase 里面是什么样子的？

A：在 HBase 中存储的当然都是 Bytes。这个问题其实就是 Bitmap 的序列化的形式，Roaring Bitmap提供了序列化和反序列化的实现，你也可以写自己的序列化/反序列化的实现。

Q：Roaring Bitmap 里这些 container 要我们自己手动的指定吗。

A：不需要，Roaring Bitmap 会自动选择使用哪个 Container。

最近整理了一套适合2019年学习的Java\大数据资料，从基础的Java、大数据面向对象到进阶的框架知识都有整理哦，可以来我的主页免费领取哦。