重新整理和理解一些重要的数学概念
极限
1.数列的极限
直观的想象一下,设{a(n)}是一个数列,如果当n趋近于无穷大时,a(n)趋近于某一个常数a,那么我们就可以认为a是数列{a(n)}的极限
2.函数的极限
2.1 自变量x趋于无穷时的极限
类似于数列的极限,因为数列本身也是一种函数,当自变量x趋于无穷时,函数值趋于某一常数值A,则称A为函数f(x)的极限。
2.2 自变量x趋于x0时的极限
如果在x→x0 的过程中,对应的函数值无限的接近常数A,那么称A就是函数f (x) 当x→x0时的极限。
完整的定义为:
设函数f (x) 在点x0的某一去心邻域内有定义,如果存在常数A,对于任意给定的正数ε(无论它多么小),总存在正数δ,使得当x满足 0 < | x – x0 | < δ时,对应的函数值f (x) 都满足不等式 | f (x) – A | < ε,那么称A就是函数f (x) 当x→x0时的极限,记作
上述概念中,x是既从x0的左侧也从x0的右侧趋向于x0。若只考虑x仅从x0的左侧趋于x0(x→x0–),或者仅从x0的右侧趋于x0(x→x0+),就可得到函数 f (x) 当x→x0的左极限,右极限。左极限和右极限统称为单侧极限。
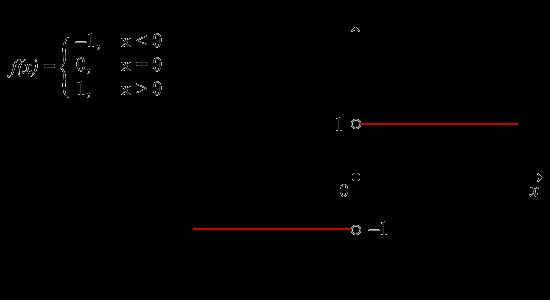
函数 f (x) 当x→x0的极限存在的充分必要条件是:左极限、右极限各自存在并相等,即 f (x0–) = f (x0+)。如下图,当x→0时f (x) 的极限是不存在的:
上图中当x趋近于0时,f(x0–)的极限为-1,f(x0+)的极限为1,所以当x→0时f (x) 的极限是不存在的。
函数的连续性
1.连续的概念
设函数y=f(x)在点x0的某一去心邻域中有定义,如果当x的变化值趋近于0时,y的变化值也趋近于0则说明函数y=f(x)在点x0处连续,也就是:
改写成极限的形式为:
函数连续需要满足3个条件:
1.函数y=f(x)在点x0处有定义
2.函数在x0处的极限存在(左极限等于右极限)
3.函数在x0处的极限等于f(x0)
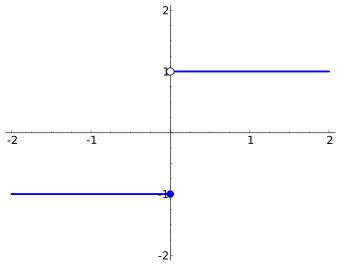
当然极限有左极限和右极限,连续也有左连续和右连续,函数的左极限等于f(x0),则称函数在x0处左连续,函数的右极限等于f(x0),则称函数在x0处右连续。
如上图所示,此函数左连续,但不是右连续。
初等函数是连续函数
2.函数的间断点
在函数不连续的情况下,由于函数间断的原因不同,我们可以将间断分为一下几类:
2.1 第一类间断点
第一类间断点函数f(x0+)和函数f(x0-)都存在,但函数不连续
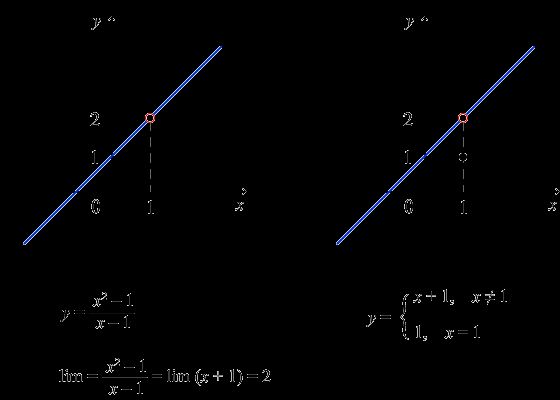
可去间断点:
f(x0+)=f(x0-)
左图中,函数 y 在 x = 1 处是没有定义的
右图中,函数 y 在 x = 1 处有定义,可极限值 ≠ 函数值
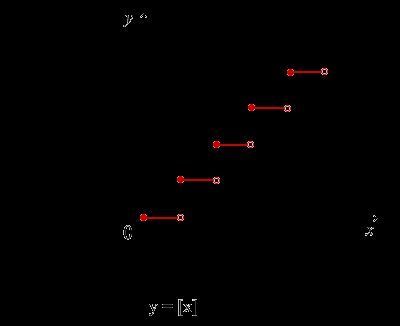
跳跃间断点:
上图表示的是不大于 x 的最大整数,每到整数点就上升跳跃
f(0+) ≠ f(0-)
2.2 第二类间断点
除了第一类间断点以外则称为第二类间断点
无穷间断点:
f(0+)和f(x0-)中至少有一个是∞,则称为x0是f(x)的无穷间断点
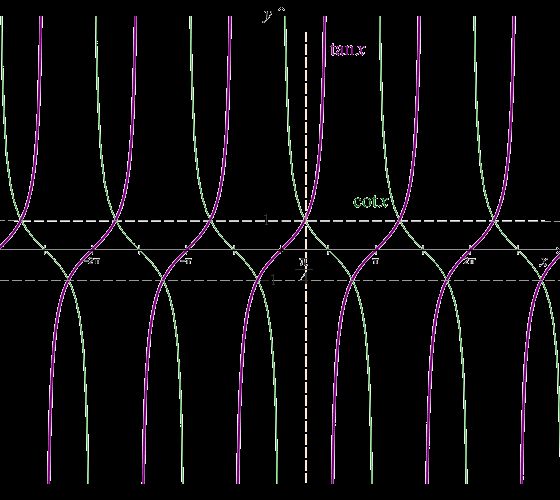
y = tan x 在 x = (π/2) + kπ 处没定义,函数的极限是无穷大 ∞
y = cot x 在 x = kπ 处没定义,函数的极限是无穷大 ∞
所以x0= (π/2) + kπ是函数y = tan x 的无穷间断点
x0= kπ是函数y = cot x 的无穷间断点
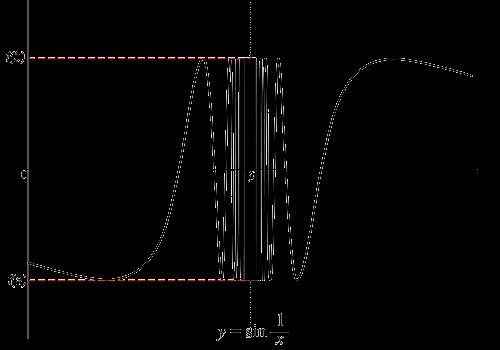
震荡间断点:
f(0+)和f(x0-)中至少有一个是不断震荡的,则称为x0是f(x)的震荡间断点
y = sin (1/x) 在 x = 0 处没定义,此时当 x→0时,函数振荡多次
由函数的连续性可以推出以下结论
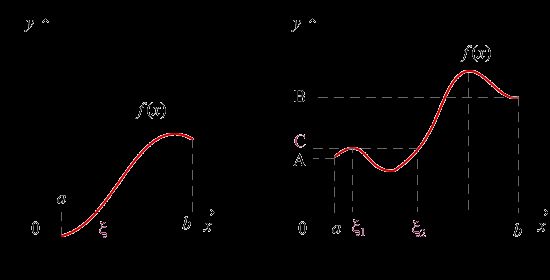
1.最值定理
由闭区间上连续函数在该区间上一定存在最大值和最小值
2.零点定理
函数f(x)在[a,b]上连续,且f(a)*f(b)<0,则在开区间(a,b)内至少存在一点x0使得f(x0)=0
概率分布的概念
设P为概率测度,X为随机变量则X的概率分布函数为:
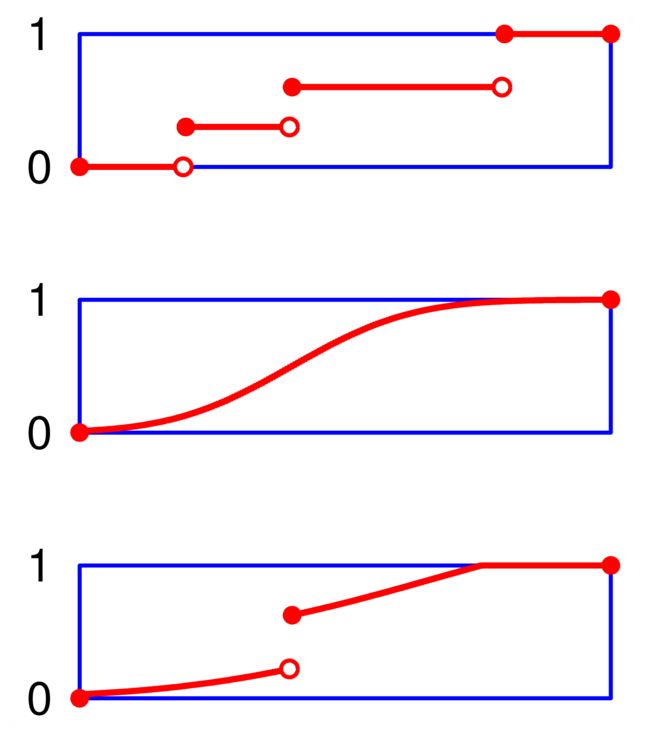
如果将X看成是数轴上的随机点的坐标,那么,分布函数F(x)在x处的函数值就表示X落在区间(-∞,x]上的概率
由此也可以看出F(X)是单调不减函数。
如上图所示,分布函数的另一个特点就是右连续性,也就是当随机变量x趋近于x0+时,函数的极限是存在的。
概率密度:
上图展示了概率密度函数f(x),其中阴影部分面积为值在a到b之间的概率。
可以看出,对概率密度的积分就是概率
如上图所示,在u处概率分布的变化最大,所以也是概率密度的最大值,u处的概率分布值为0.5说明P(x<=u)为0.5
参考资料
http://math001.com/limit_function/