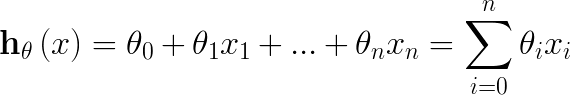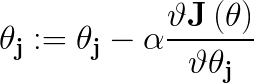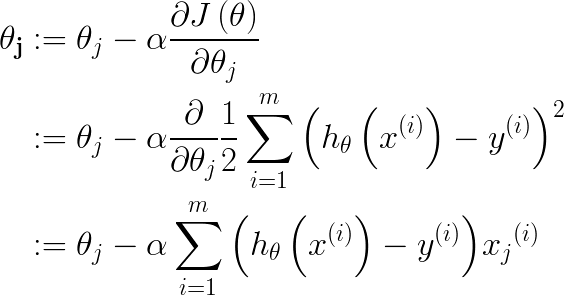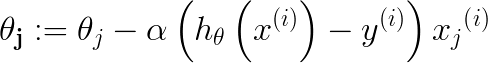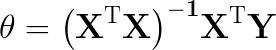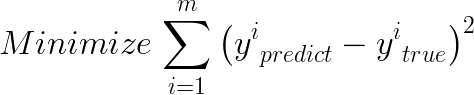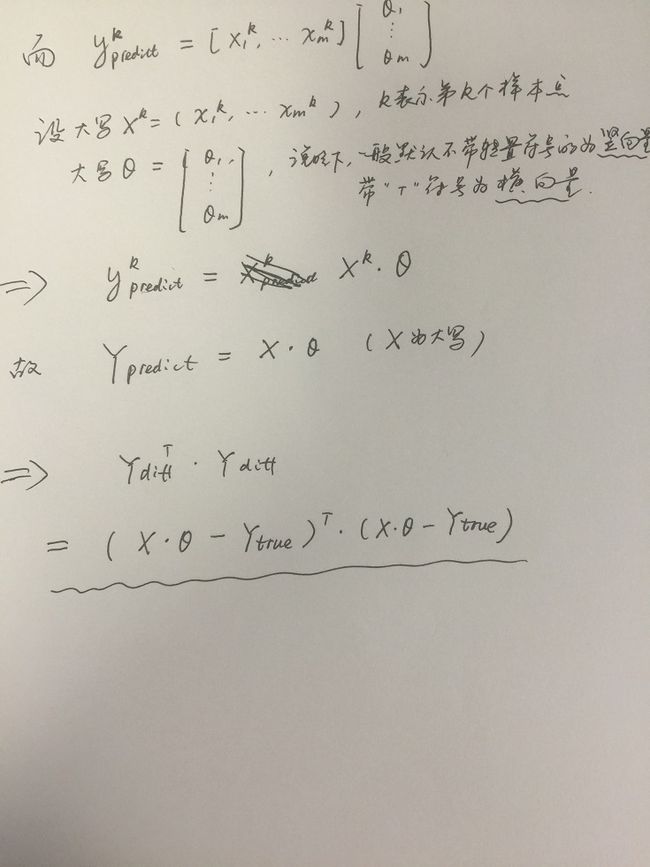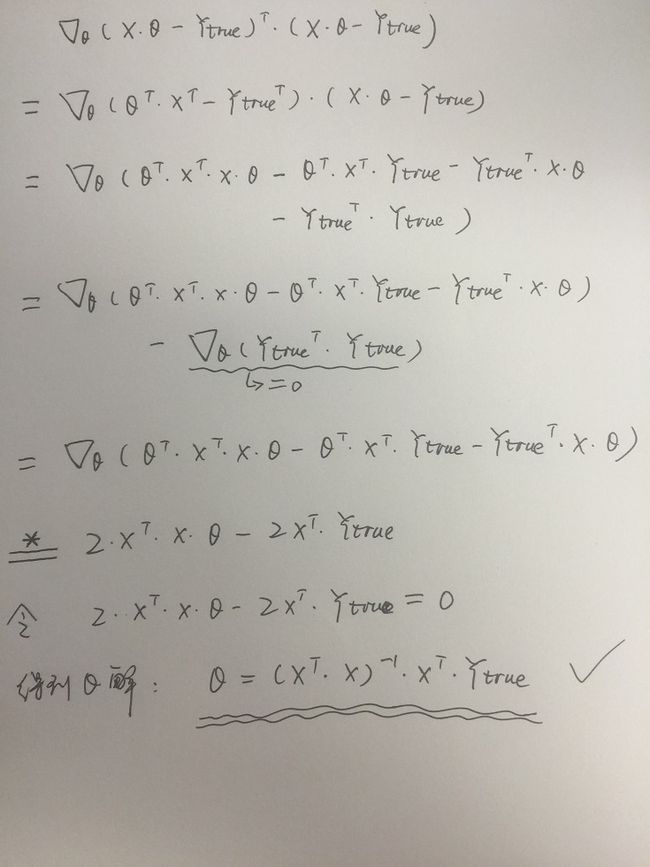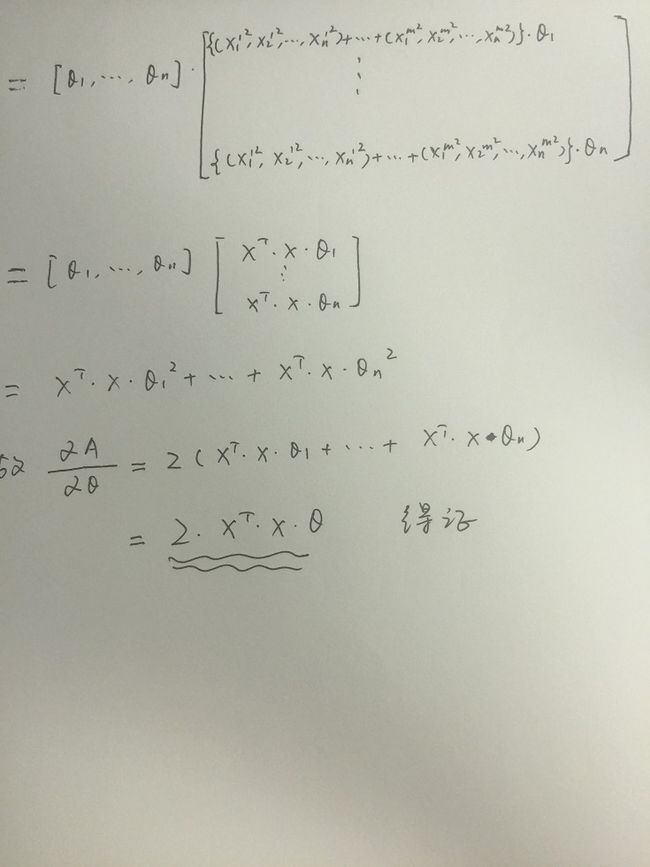这里直接从课程的第二课开始,其实视频里的第一课Andrew(为了方便阅读和书写,以后都把Andrew Ng简称为Andrew了,没有不敬的意思,希望他的粉丝或者读者勿喷)主要是分享了机器学习的一些故事和应用场景,总的来说就是机器学习已经贯穿到生活的点点滴滴,每行每业,会点机器学习的同志是很高大上的(现在回过头看Andrew的话,还是很有预见性的,IT工程师不会点机器学习真不好意思跟人打招呼)
线性回归
顾名思义,线性回归就是用一条线(线性)拟合(回归)数据分布,在最简单的2维平面中,这种拟合关系体现为一元一次方程:
θ0代表截距,θ1代表x1的系数,这个就是我们接触到的最早的线性函数表达式了。扩展一下,将2维扩展到多维(假设为n维)情况,就成了线性回归的一般表达式了:
为了简单书写,上式最后写成了和符号∑形式。
损失函数
线性回归函数只是定义了模拟我们数据分布的关系式,那剩下的问题是我们如何求解系数(或者可以称之为权重)?大部分童鞋肯定知道一元方程如何求解,只要拿数据中的两个point值,带入到方程中解二元一次方程组就能解的θ0和θ1,但是在线性回归中有两个现实的问题,第一所有点未必真的都乖乖的落在我们拟定的线性路径上,第二就是回归本质上是一个预测问题,如果按照求解方程组的方式来求解系数,会导致不同的样本有不同的系数,所以充分考虑问题的本质是“拟”和“预测”,我们并不是真的要求出某个样本的一个系数组合,而是找出一个能预测所有样本(已知或者未来可能出现的)的函数,故定义了回归函数之后,我们需要一个叫做【损失函数】的东东来评估回归函数的训练求解误差,当和样本的误差在我们认定可接受的范围内的时候,就可以考虑接受当前求解到的一组系数。
由于在第一课中Andrew Ng并没有提到损失函数的大小好坏的评判标准,这里先顺带提一句,损失函数并不是越小越好(>= 0),正如我上面说的,损失函数值越小可能会带来的副作用是预测能力下降(过拟合问题,对样本描述的越精确,函数的泛化能力也越弱)
Andrew选择的损失函数是Mean Square Loss(Or Mean Square Error):
看到这里,我相信机器学习初学者肯定会有一个问题,为什么选择<差平方的均值>啊?为什么不直接用<差绝对值的均值>呢,其实有实际应用中有很多的损失函数,差的平方,差的绝对值,logistic损失等等,这个里面也有很大的学问,这里不展开讨论,有时间再写一些关于这方面的笔记,暂且认为我们只有一种评价损失的函数,就是MSE。
好,看到这里,我们已经有一个很明确的损失函数方程了,回想下我们的目标,即“训练出一个可以拟合当前数据分布的最优函数”,什么是最优?能使得损失函数最小的分布函数就是最优拟合函数,换言之,我们本来的目标是得到【最优线性拟合函数】,现在变成了【最小化损失函数】(其实这一步可以认为是一种问题建模,将实际问题转变成可以求解的量化问题),即:
梯度下降
有了量化的最小化损失函数,接下来需要找一种方法求解这个函数,这里顺带提醒一句,损失函数是以【参数θ】为自变量的函数,不是样本点x,这个应该很好理解,我们最终的目的是求出符合数据分布的参数,只要参数确定了,方程就确定了。Andrew给出的解决方案是【梯度下降】,即先随便先设置一组θ值,然后每次迭代朝着梯度下降最大的方向更新θ值(有可能增加也可能减少,方向是朝着最优的方向),直到J(θ)达到我们设置的阈值或者在一定范围内不再变化为止。
为什么【梯度下降最大】的方向就是最优解的方向呢(注意一定是下降最大的方向,设想空间中的一点,它的四周都是梯度,而下降最大的梯度方向才是我们要找寻的)?一定能达到局部最优或者是全局最优么?这里先暂时不讨论这两个问题,姑且认为这是一种被证明过的求解最优化问题的方法。那么如何求解呢 ?迭代公式如下:
如Andrew视频中所说,符号“:=”是赋值更新的含义,将“:=”右边的值赋给左边的变量,而“=”指的是一种等式变化的断言,“a=b”表示a就是等于b,或者a可以等值变化成b,α是学习率,可以理解为参数朝着梯度方向的单位步长,从公式中可以看出所谓的【梯度下降】方向就是每个参数θ的偏导数方向,下面具体列出下求导的过程:
公式3.2中,m代表有m个样本点,j代表某个向量的第j个维度,对于θ来说,θj代表第j个参数,对于x向量来说,xj代表第j维的值,从公式中可以得出两个信息,一个是每次迭代,θj是通过对应维度上的x值来作为调整因子的,另一个是每次θ更新都要计算样本中的所有点。
Andrew称上面的梯度下降求解为batch gradient descent,即每次需要计算样本中所有点来迭代更新参数θ值,为了方便快速的迭代,可以采用一种称为stochastic gradient descent【随机梯度下降】的方法,每次选取某一个点作为参数更新的输入,如公式3.3所示:
可见每个维度θj的迭代只需要计算某个点的y值差和相应维度的xj乘积,速度大大提高了,那为啥还需要批量梯度下降算法呢,都用随机梯度下降不就完了? 这里稍微总结了下这两个算法的主要区别:
- SGD(随机梯度下降)每次结果不是确定的,因为每次更新都是随机挑选一个点作为更新的依据,而BGD(批量梯度下降)在初始参数输入一定的情况下,运行的结果永远都是固定的。
- BGD往往能找到局部或者全局最优解,而SGD很可能在最优解附近徘徊震荡
- SGD由于其随机性,往往能避免陷入到局部极值中,而BGD容易陷入到局部极值中
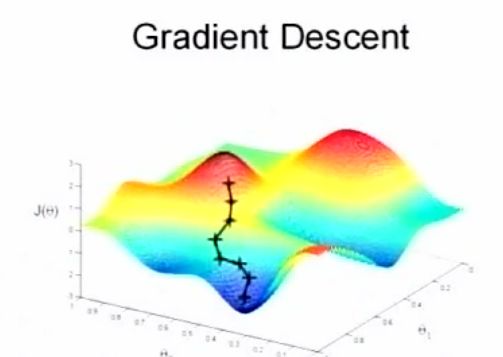
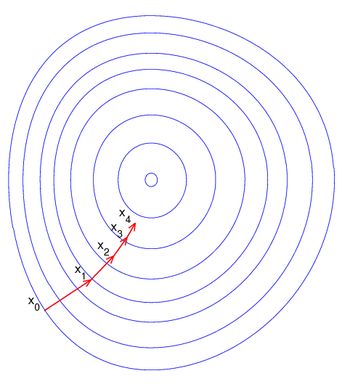
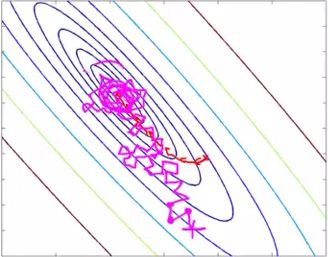
这里贴两张Andrew课中的图来形象化展示BGD和SGD的求解过程:
将3D的模型画成平面等高线的话如下:
而SGD的等高线应该是:
利用矩阵求解参数(Normal Equation)
在课中,Andrew最后还介绍了一个利用矩阵来直接求解参数的方法(不用迭代),估计很多人看的云里雾里,因为Andrew写了很多定律,比如矩阵的偏导数公式,trace的定义,trace矩阵时的一些特性公式,这里不再赘述Andrew的求解过程,而是从另外一个大家都熟知的方法得到Andrew最后给出的参数结果等式,即【最小二乘法】,什么?!!原来Andrew列了那么多就是最小二乘法啊,且看下面我的求解:
课中最后给出的参数解:
最小二乘法求解:
经典最小二乘法的定义式如下:
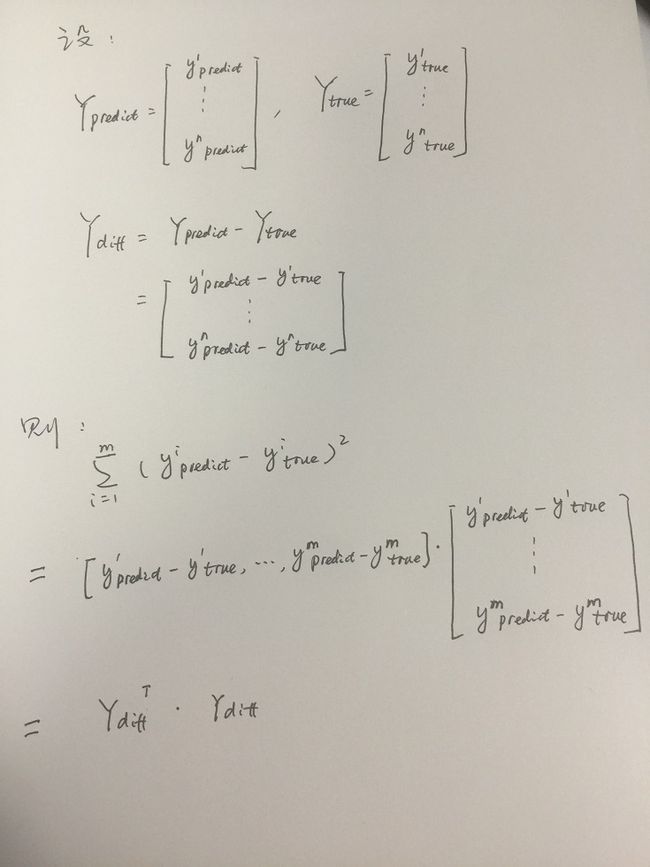
对公式求导得到极值点便是参数θ的解析解(联系我们小时候学过的求极值方法,不就是求导么_,但是注意不是每个函数都能求导的哦,这个就不在这详细说了),详细过程如下(这里用手写的图片了,大家凑合看吧,顺便吐槽下,不支持在线编辑latex简直是灾难啊!!比zybuluo弱爆了!!):
带*号的那一段等式是矩阵求导的范畴,如果有不懂的可以详细去看看矩阵如何求导的,这里举一个例子来说明下:
由此,所有证明完毕,可见通过最小二乘法的矩阵运算也能得到和Andrew课中一样的结论。