本系列教程来源于出版设计《基于MATLAB编程基础与典型应用书籍》,如涉及版权问题,请联系:[email protected]。 出版社:人民邮电出版社, 页数:525。
本系列教程目前基于MATLABR2006a,可能对于更高级版本的功能和函数有差异,教程中如有问题,请联系:[email protected]
3.4 稀疏矩阵
在实际应用中经常会使用这样的矩阵,该矩阵中包含的很多元素值为0,这样的矩阵被称为稀疏矩阵(Sparse Matrix)。因为稀疏矩阵大部分的元素都是0,所以只需要储存非零元素的下标和元素值,这种特殊的存储方式可以节省大量的存储空间和不必要的运算。MATLAB提供了多个对稀疏矩阵进行操作的函数。
如果全元素矩阵不经过专门的定义是不能产生稀疏矩阵的,最简单的创建稀疏矩阵的函数为sparse,可以将全元素矩阵转化为稀疏矩阵;与之相反,可以调用函数full将稀疏矩阵转变为全元素矩阵。下面将介绍稀疏矩阵的一些相关操作。
3.4.1 稀疏矩阵的创建
MATLAB提供了几个函数来创建稀疏矩阵,具体调用格式如表3.8所示。
表3.8 稀疏矩阵的创建函数
| 函数名 | 功能 |
|---|---|
S = sparse(A) |
将矩阵A转化为稀疏矩阵形式,即由A的非零元素和下标构成稀疏矩阵S。若A本身为稀疏矩阵,则返回A本身 |
S = sparse(m,n) |
生成一个m×n的所有元素都是0的稀疏矩阵 |
S = sparse(i,j,s) |
生成一个由长度相同的向量i、j和s定义的稀疏矩阵S,其中i、j是整数向量,定义稀疏矩阵的元素位置(i,j),s是一个标量或与i,j长度相同的向量,表示在(i,j)位置上的元素 |
S = sparse(i,j,s,m,n) |
生成一个m×n的稀疏矩阵,(i,j)对应位置元素为si,m = max(i)且n =max(j) |
S= sparse(iiI,j,s,m,n,nzmax) |
生成一个m×n的含有nzmax个非零元素的稀疏矩阵S,nzmax的值必须大于或者等于向量i和j的长度 |
[B,d] = spdiags(A) |
从矩阵A中提取所有非零对角元素,这些元素保存在矩阵B中,向量d表示非零元素的对角线位置 |
B = spdiags(A,d) |
从A中提取由d指定的对角线元素,并存放在B中 |
A = spdiags(B,d,A) |
用B中的列替换A中由d指定的对角线元素,输出稀疏矩阵 |
A=spdiags(D,k,m,n) |
矩阵D的每一列代表矩阵的对角线向量;k代表对角线的位置(0代表主对角线,-1代表向下位移一单位的次对角线,1代表向上位移一单位的次对角线,依此类推);m、n分别代表矩阵的行、列维数 |
【例3.42】产生稀疏矩阵
首先在MATLAB命令行窗口中输入以下命令,创建一个5阶的单位对角阵:
>> a=eye(5) %生成5阶的单位对角阵
按照以下命令行修改矩阵a中最后一行的元素值:
>> a(6,:)=[2 0 0 3 0] %修改矩阵a中最后一行的元素值
使用函数sparse将上面的矩阵a转化为稀疏矩阵,在命令窗口输入:
>> b=sparse(a) %使用函数sparse将上面的矩阵a转化为稀疏矩阵
结果如下:
b = (1,1) 1 (6,1) 2 (2,2) 1 (3,3) 1 (4,4) 1 (6,4) 3 (5,5) 1
3.4.2 将稀疏矩阵转化为全元素矩阵
可以使用full函数可以将稀疏矩阵转化为全元素矩阵,该函数的调用格式如下:
① A=full(S) S为稀疏矩阵,A为全元素矩阵
【例3.46】将稀疏矩阵转化为全元素矩阵
>> a=eye(6) %生成6阶的对角阵
使用函数sparse将矩阵a转化为稀疏矩阵,在命令窗口中输入以下内容:
>> b=sparse(a) % 使用函数sparse将矩阵a转化为稀疏矩阵
如将稀疏矩阵b转化为原来的全元素矩阵,可以使用函数full,在命令窗口输入:
>> full(b) % 将稀疏矩阵b转化为原来的全元素矩阵
3.4.3 矩阵中非零元素的查找
对任意一个矩阵,使用函数find可以查找出非零元素的位置及其值。该函数的调用格式如下:
① k = find(X)
② [i,j] = find(X)
③ [i,j,v] = find(X)
其中,命令①按行检索X中非零元素的点,若没有非零元素,将返回空矩阵,命令②检索X中非零元素所对应的行标号i和列标号j;命令③检索X中非零元素所对应的行标号i和列标号j以及位置(i, j)对应的元素值v。
【例3.47】矩阵中非零元素的查找
首先在命令窗口中输入以下内容,将单位矩阵a转化为稀疏矩阵b。
>> a=eye(6); %创建6阶的对角单位阵
>> b=sparse(a) %讲单位阵转化为稀疏矩阵
①若检索稀疏矩阵b中非零元素的行标i和列标j以及对应的元素值v,在命令窗口输入:
>> [i,j,v]=find(b)
②若检索全元素矩阵a中非零元素的行标i和列标j以及对应元素值v,在命令窗口输入:
>> [i,j,v]=find(a)
3.3.4 其他稀疏矩阵的创建方法
MATLAB除了上面介绍的基本创建稀疏矩阵的方法外,还提供了几个函数可以直接创建特殊的稀疏矩阵,具体调用格式如表3.9所示。
表3.9 稀疏矩阵的其他创建函数
| 函数名 | 功能 |
|---|---|
S = speye(m,n) |
生成m×n的单位稀疏矩阵 |
S = speye(n) |
生成n×n的单位稀疏矩阵 |
R = sprand(S) |
生成与S具有相同稀疏结构的均匀分布随机矩阵 |
R = sprand(m,n,density) |
生成一个m×n的服从均匀分布的随机稀疏矩阵,非零元素的分布密度是density |
R = sprand(m,n,density,rc) |
生成一个近似的条件数为1/rc、大小为m×n的均匀分布的随机稀疏矩阵 |
R = sprandn(S) |
生成与S具有相同稀疏结构的正态分布随机矩阵 |
R = sprandn(m,n,density) |
生成一个m×n的服从正态分布的随机稀疏矩阵,非零元素的分布密度是density |
R = sprandn(m,n,density,rc) |
生成一个近似的条件数为1/rc、大小为m×n的均匀分布的随机稀疏矩阵 |
R = sprandsym(S) |
生成稀疏对称随机矩阵,其下三角和对角线与S具有相同的结构,其元素服从均值为0、方差为1的标准正态分布 |
R = sprandsym(n,density) |
生成n×n的稀疏对称随机矩阵,矩阵元素服从正态分布,分布密度为density |
R = sprandsym(n,density,rc) |
生成近似条件数为1/rc的稀疏对称随机矩阵 |
R= sprandsym(n,density,rc,kind) |
生成一个正定矩阵,参数kind取值为kind=1表示矩阵由一正定对角矩阵经随机Jacobi旋转得到,其条件数正好为1/rc;kind=2表示矩阵为外积的换位和,其条件数近似等于1/rc;kind=3表示生成一个与矩阵S结构相同的稀疏随机矩阵,条件数近似为1/rc ,density被忽略 |
【例3.48】其他稀疏矩阵的创建
①使用函数sparse创建行数从2至16,列数从3至17,值为4至18的稀疏矩阵。在命令窗口输入以下内容:
>> S=sparse(2:16,3:17,4:18) %创建行数从2至16,列数从3至17,值为4至18的稀疏矩阵
②如要生成与矩阵S具有相同稀疏结构的均匀分布随机矩阵,可以使用函数sprand。在命令窗口输入:
>> R = sprand(S)
③若要生成与S具有相同稀疏结构的正态分布随机矩阵,可以使用函数sprandn。在命令窗口输入:
>> G = sprandn(S)
④若要生成稀疏对称随机矩阵,其下三角和对角线与S具有相同的结构,其元素服从均值为0、方差为1的标准正态分布,可以使用函数sprandsym。在命令窗口输入:
>> F = sprandsym(S)
⑤若要生成n×n的单位稀疏矩阵,可以使用函数speye。在命令窗口输:
>> K = speye(6)
注意:由上例可以看出,此查找语句适合于稀疏矩阵,也适合于一般矩阵。
3.4.5 稀疏矩阵中非零元素信息的查看
前面介绍了使用find函数可以查看全元素矩阵和稀疏矩阵的非零元素的位置及值,对于稀疏矩阵来说,MATLAB还提供了其他几个函数用来查看稀疏矩阵中的信息,具体调用格式如表3.10所示。
表3.10 稀疏矩阵的信息查看函数
| 函数名 | 功能 |
|---|---|
n = nnz(X) |
返回矩阵X中非零元素的个数 |
s = nonzeros(A) |
返回矩阵A中非零元素按列顺序构成的列向量 |
k = nzmax(A) |
返回分配给稀疏矩阵中所有非零元素存储单元的个数 |
S = spalloc(m,n,nzmax) |
产生一个m×n阶只有nzmax个非零元素的稀疏矩阵,这样可以有效减少存贮空间和提高运算速度 |
f = spfun('function',S) |
用函数'function'对S中非零元素求值,如果'function'不是对稀疏矩阵定义的,同样可以求值 |
R = spones(S) |
将稀疏矩阵S中的非零元素全换为1 |
【例3.49】稀疏矩阵中非零元素信息的查看
>> S=sparse(2:16,3:17,4:18) %创建行数从2至16,列数从3至17,值为4至18的稀疏矩阵
①若要查看矩阵S中非零元素的个数,可在命令窗口输入:
>> n = nnz(S)
②若要返回矩阵S中非零元素按列顺序构成的列向量,可在命令窗口输入:
>> s = nonzeros(S)
③若要返回分配给稀疏矩阵中所有非零元素存储单元的个数,可在命令窗口输入:
>> k=nzmax(S)
④用函数'exp'对S中非零元素求值,在命令窗口输入:
>> f= spfun('exp',S)
3.4.6 用图形方式查看稀疏矩阵的信息
将稀疏矩阵中非零元素的分布用图形方式显示,特别适用于较大的稀疏矩阵及图形处理过程中的分析。MATLAB的函数spy提供了一个用图形显示稀疏矩阵非零元素的模板,图形中的每个点表示稀疏矩阵中非零元素的位置。该函数的调用格式如下:
①spy(S)
②spy(S,markersize) markersize为整数,指定点阵大小,其他参数与上相同
③spy(S,'LineSpec')
④spy(S,'LineSpec',markersize)
其中①画出稀疏矩阵S中非零元素的分布图形,S也可以是全元素矩阵;②命令中markersize为整数,指定点阵大小,其他参数与①相同;③'LineSpec'指定绘图标记和颜色。
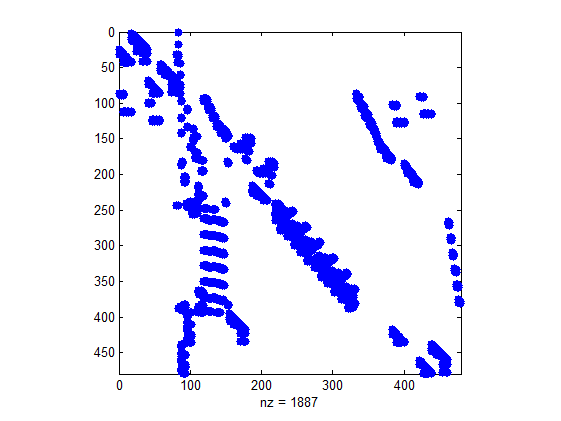
【例3.50】用图形方式查看稀疏矩阵的信息
>> load west0479 %向工作空间导入west0479数据
>> A=west0479;
>> spy(A) %画出稀疏矩阵A中非零元素的分布图
结果如图3.1所示。
>> spy(A,20) %修改点的大小
结果如图3.2所示。
3.4.7 矩阵排序
稀疏矩阵多用于较大的矩阵,MATLAB因此提供了几个矩阵排序函数,有些可以达到降低计算时间的效果,具体调用格式如表3.11所示。
表3.11 稀疏矩阵的排序函数
| 函数名 | 功能 |
|---|---|
p = colamd(S) |
返回稀疏矩阵S的列的近似最小度排序向量p |
p = colmmd(S) |
返回稀疏矩阵S的列的最小度排序向量p,按p排列后的矩阵为S(: , p) |
j = colperm(S) |
返回一个稀疏矩阵S的列变换的向量。列按非0元素升序排列。有时这是LU分解前有用的变换:LU(S(:,j))。如果S是一个对称矩阵,对行和列进行排序,有利于Cholesky分解:chol(S(j,j)) |
p = dmperm (A) |
返回A的行排列向量p,这样,如果A满列秩,就使得A(p,:)是具有非0对角线元素的方阵 |
[p,q,r] = dmperm(A) |
A为方阵,p为行排列向量,q为列排列向量,使得A(p,q)是上三角块形式,r为索引向量 |
[p,q,r,s] = dmperm(A) |
A不是方阵,p,q,r含义与前面相同,s也是索引向量 |
p = randperm (n) |
对正整数1,2,3,…,n的随机排列,可以用来创建随机变换矩阵 |
p = symamd(S) |
S为对称正定矩阵,返回排列向量p |
r = symrcm (S) |
返回S的对称逆Cuthill-McKee排序r,使S的非0元素集中在主对角线附近 |
p = symmmd(S) |
返回S的对称最小度排列向量p,S为对称正定矩阵 |
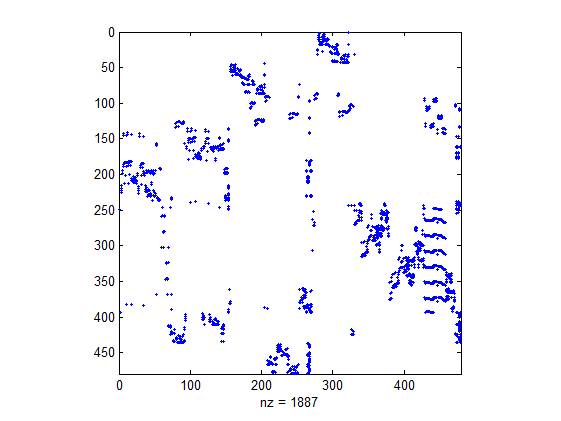
【例3.51】比较稀疏矩阵S与排序后的矩阵p
>> load west0479; %导入数据
>> S=west0479;
>> p=colmmd(S); %稀疏矩阵S的列的最小度排序向量p,按p排列后的矩阵为S(: , p)
>> spy(S(:,p)) %画出稀疏矩阵S(: , p)中非零元素的分布图
【例3.52】比较稀疏矩阵S与排序后的矩阵p
>> A=sprandsym(200,0.03)+100*speye(200,200) %生成系数矩阵
>> p=symmmd(A) %计算矩阵A的对称最小度排列向量p
>> spy(A) %画出稀疏矩阵A中非零元素的分布图
结果如图3.4所示。
>> spy(A(p,p)) %画出排序后稀疏矩阵A中非零元素的分布图
结果如图3.5所示。
注意:指令symmmd采用最小度排序算法,其中心思想是根据消元的每个阶段和选取可能的主元,获得填充项和运算次数的最小化,因而列高斯消元法能够与最小度算法较好地结合。
3.5 本章小结
本章重点介绍了矩阵的相关运算,包括矩阵的基本运算、矩阵的各种分解运算、稀疏矩阵的相关运算以及线性方程组的求解。
矩阵的基本运算部分使用大量的实例介绍了矩阵的四则运算、矩阵的乘方、矩阵的转置以及一些矩阵函数的使用方法,同时将矩阵和数组的运算进行比较,以便加深读者对矩阵和数组运算的区别的理解。另外该部分还使用实例介绍了矩阵的关系操作和逻辑操作。
矩阵的分解部分使用大量的实例介绍了经常使用的MATLAB提供的矩阵的各种分解函数的使用,包括矩阵的LU分解、奇异值分解、特征值分解、Cholesky分解、QR分解、Schur分解等。矩阵的分解是矩阵运算的重要部分,在实际的工程应用中经常会使用,因此掌握矩阵分解对解决实际问题是很有帮助的。
线性方程组的求解是解决线性问题时经常遇到的问题,本章使用实例对该线性方程组的求解方法进行了系统的介绍,重点介绍了使用矩阵LU分解、Cholesky分解和QR分解来求解线性方程组的方法。在求解大型方程组时使用矩阵分解的方法来求解方程组解很有用,其优点是运算速度快、可以节省磁盘空间、节省内存。
最后本章介绍了稀疏矩阵的相关操作,包括稀疏矩阵的创建、稀疏矩阵的元素信息的查看、稀疏矩阵的排序等。使用大量的实例介绍了稀疏矩阵创建函数的使用以及稀疏矩阵的元素相关信息的查看函数的使用等内容。
作者:德特数据
联系方式:[email protected]