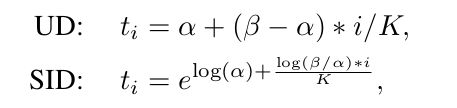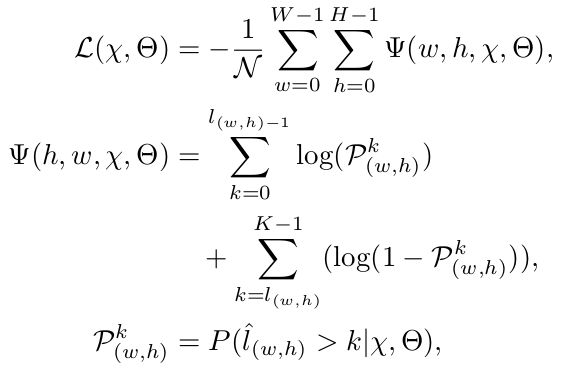论文地址:[1806.02446] Deep Ordinal Regression Network for Monocular Depth Estimation
概述
Monocular depth estimation (MDE), 从理论上是一个病态的问题,近年来的工作利用 deep convolutional neural networks (DCNN) 提取 image-level information 及 hierarchical features 在 MDE 问题上取得了巨大的提升。这些方法把 MDE 视为一种 regression problem,并把 mean squared error (MSE) 作为 regression loss,MSE 的显著缺点是收敛速度慢且容易陷入局部极值。因此,Huan Fu 等人提出一种基于 ordinal regression的方法解决 MDE 问题,即 deep ordinal regression network (DORN)。
这篇文章的主要贡献包括:
(1)引入 ordinal regression 处理 MSE 问题,并采用 spacing-increasing discretization (SID) 方法量化深度
(2)采用 dilated/atrous convolution 提高 feature map 分辨率
(3)设计一种 full-image encoder 并结合 atrous spatial pyramid pooling (ASSP) 作为 scene understanding 模块
网络结构
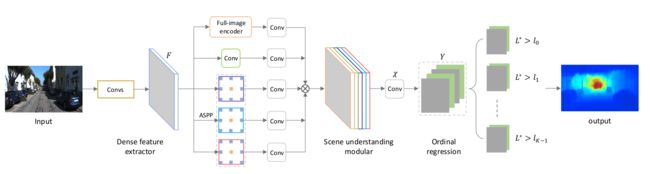
输入图片经由 dense feature extractor (resnet 101) 提取 feature map F,并送入三个分支,full-image encoder,cross-channel learner (绿色 Conv) 和 ASSP ,其结果在 channel 上 concatenate,此 feature map 经过 kernel size 为1的卷积 point-wise regress,其结果经过 softmax 转化为概率形式,train 过程中计算 ordinal regression loss,inference 阶段采用另外一种形式获得 prediction 结果。
Full-image encoder
假设 feature map F 为 (B, C, W, H) 结构,首先进行 window size 为k的 average pooling,后接 fully connected layer (fc) 并输出C维向量,视其 (B, C, 1, 1) 的 tensor,broadcast 为 (B, C, W, H) 即原 feature map 尺寸。
Spacing-increasing discretization
SID 的动机是在实际任务中,depth 越大,对其估计误差的容忍就越大,因此对 depth 取 log 后均匀量化可以满足这个目的,具体地:
UD为 uniform discretization 均匀量化,其中t为量化阈值,i为量化阶,alpha 和 beta 是 depth 上下界限,为了避免除0,depth 需要加上一个 shift 以保证 alpha 为1,量化阶的总数记为K
Ordinal Regression
ordinal regression 在 train 与 inference 过程中 predict 的方式不同
其中L为 loss,l(w,h) 表示在 (w, h) 点的 depth,不加 hat 为 ground truth,否则为 predict (但这只是概念上的),N为W与H的乘积。
可以采用下述流程计算:
假设 scene understanding module 的输出为 (B, C, W, H),首先通过 kernel 为1的卷积得到 (B, 2K, W, H),reshape 为 (B, 2, K, W, H) 并在 axis=1 上计算 softmax 获得 (B, 2, K, W, H) 的 tensor,axis=1 上,取0表示:batch 内b图片在 feature map 的 (w, h) 位置上的特征点进行预测,其关联的 depth (ground truth depth) 量化后的数值不大于k的概率,取1表示大于k的概率。对预测结果 tensor (B, 2, K, W, H) 只取大于k的概率,得到 tensor (B, K, W, H),记为y,loss = sum( - log(ay + b)),其中a可以通过如下方式获得,假设点 (b, w, h) 所对应的 depth 量化为k,这样生成一个长度为K的向量,其0...k-1的元素都为1,k及之后为-1,由于共有(B, W, H)个这样的向量,因此可以组成 tensor a,shape 与 y一致,b的生成方式类似a,不过其0...k-1的元素都为0,k及之后为1。
inference 时,对点 (b, w, h),只需要计算向量 (b, :, w, h) 中大于0.5的元素个数即可获得预测 depth 的量化值