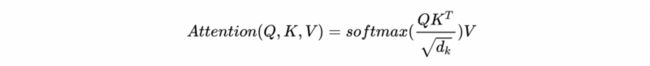在「拆 Transformer 系列一:Encoder-Decoder 模型架构详解」中有简单介绍 Attention,Self-Attention 以及 Multi-Head Attention,都只是在直观上介绍 Attention 的作用,如何能够像人的视觉注意力机制那样,记住关键信息,并且也介绍了 Self-Attention 机制如何能通过对自身注意力加权来学习句子内部结构以及一些语法特征。
现在,我还要打算继续详细讲解 Attention,主要讲解 Transformer 中的 Multi-Head Attention 如何实现?通过图解加说明来讲解。
Self-Attention
上一节我们讲到,Self-Attention 的 Query=Key=Value,即 Q,K,V 三个矩阵都来自同一个输入,而 Attention 计算过程如何呢?
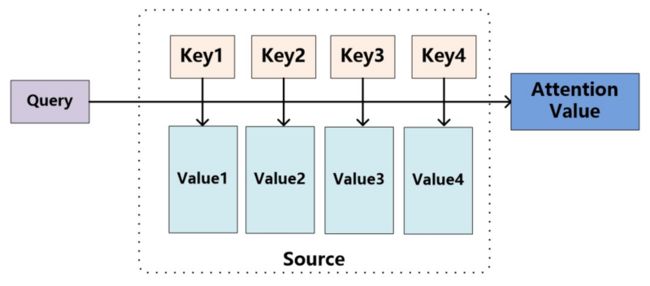
Attention 机制实质上就是一个寻址过程,通过给定一个任和务相关的查询 Query 向量 Q,通过计算与 Key 的注意力分布并附加在 Value 上,从而计算 Attention Value,这个过程实际上是 Attention 缓解神经网络复杂度的体现,不需要将所有的 N 个输入都输入到神经网络进行计算,而是选择一些与任务相关的信息输入神经网络,与 RNN 中的门控机制思想类似。
Attention 机制计算过程大致可以分成三步:
① 信息输入:将 Q,K,V 输入模型
- 用 $X=[x_1,x_2,...x_n]$ 表示输入权重向量
② 计算注意力分布 α:通过计算 Q 和 K 进行点积计算相关度,并通过 softmax 计算分数
- 另 $Q=K=V=X$,通过 softmax 计算注意力权重,$α_i=softmax(s(k_i,q))=softmax(s(x_i, q))$
我们将 $α_i$ 称之为注意力概率分布,$s(x_i, q)$ 为注意力打分机制,常见的有如下几种:
- 加性模型:$s(x_i,q)=v^Ttanh(Wx_i+Uq)$
- 点积模型:$s(x_i,q)=x_i^Tq$
- 缩放点积模型:$s(x_i,q)={x_i^Tq}/\sqrt{d_k}$
- 双线性模型:$s(x_i,q)=x_i^TWq$
③ 信息加权平均:注意力分布 $α_i$ 来解释在上下文查询 $q_i$ 时,第 $i$ 个信息受关注程度。
$att(q,X)=\sum_{i=1}^N{α_iX_i}$
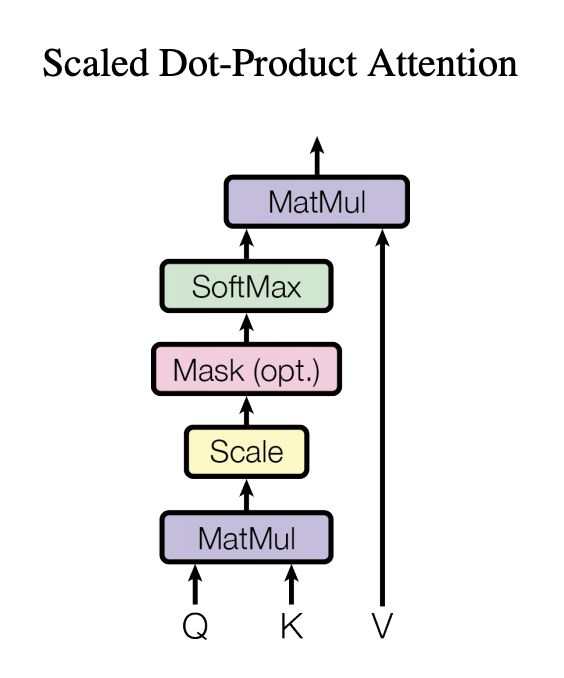
上面讲述了 Attention 的通用计算过程,也讲述了注意力分数计算的多种选择,那么在 Transformer 中,采用哪种呢?答案就是:Scaled Dot-Product Attention
上图所示就是 Scaled Dot-Product Attention 的简图,可以看到输入的 Q,K,V 都相同。
可以看到 Scaled Dot-Product Attention 有个缩放因子 $\sqrt{d_k}$,为什么要加这个缩放因子呢?
如果 $d_k$ 很小, additive attention 和 dot-product attention 相差不大。但是如果 $d_k$ 很大,点乘的值很大,如果不做 scaling,结果就没有 additive attention 好。
另外,点乘结果过大,使得经过 softmax 之后的梯度很小,不利于反向传播,所以对结果进行 scaling。
我们在上一节中简单提到 Self-Attention 能够捕获长距离依赖,并且能够学习到句子内部结构及语法,那么 Self-Attention 的计算流程又是如何呢?
Step 1
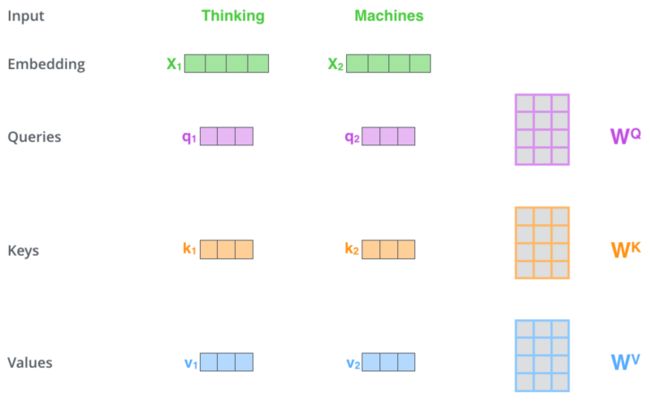
首先给出信息输入:用 $X=[x_1,x_2,...x_n]$ 表示 $N$ 个输入信息,通过线性变换得到 Q,K,V 三个向量的初始表示:
$Q=W_qX$$K=W_kX$
$V=W_vX$
Step 2
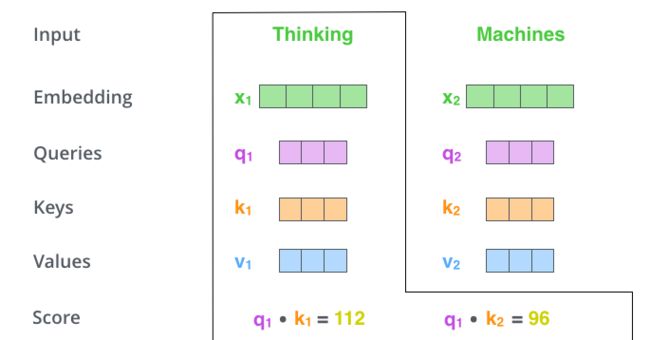
计算自注意力得分,假设我们正在计算下图中的第一个单词 “ Thinking” 的自注意力,则我们需要计算 “Thinking” 这个单词对句子中每个单词的评分。分数决定了当我们在某个位置对单词进行编码时,要在输入句子的其他部分上投入多少注意力。
通过将 Q 和 各个单词的关键字向量 K 进行点积计算分数,因此,如果我们正在处理位置 #1 上的单词的自我注意,则第一个分数将是 $q_1$ 和 $k_1$ 的点积。第二个分数是 $q_1$ 和 $k_2$ 的点积。
$q_1.k_1=112,q_1.k2=96$
Step 3
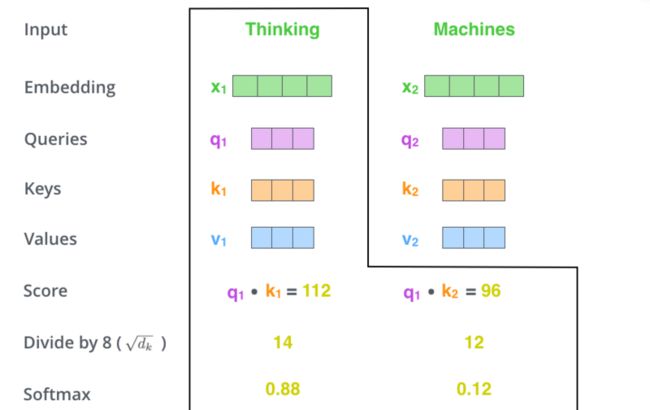
对 Step 2 中计算的分数进行 Scale,这里通过除以 8 ( 论文中 $d_k=64$,这可以让模型有更稳定的梯度,默认值是 64,也可以是其它值 ),将结果进行softmax 归一化。
$z_1=q_1.k_1/\sqrt{d_k}=112/\sqrt{64}=112/8=14,z_2=q_1.k_2/\sqrt{d_k}=96/\sqrt{64}=96/8=12$
$softmax(z_1)=exp(z_1)/\sum_{i=1}^2(exp(z_i))=0.88,softmax(z_2)=exp(z_2)/\sum_{i=1}^2(exp(z_i))0.12$
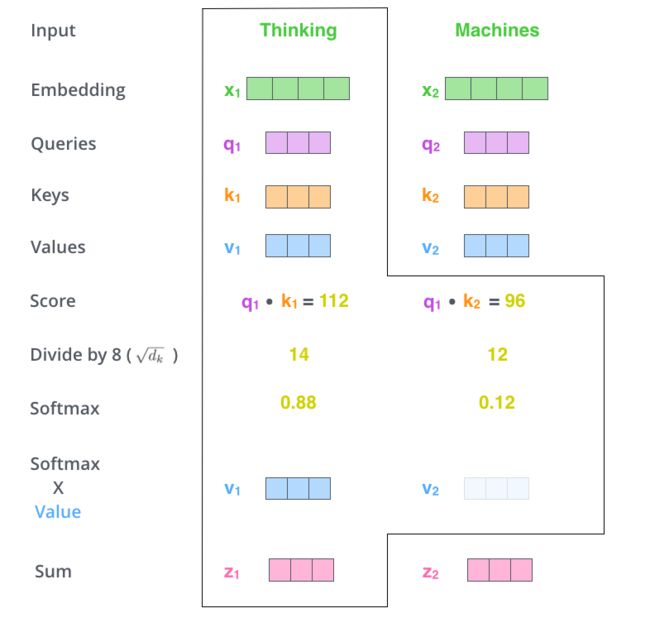
Step 4
利用得分分别乘以 $v_1,v_2$ 后得到一个加权后的值,将这些值加起来得到 $z_1$。这就是这一层的输出,仔细感受一下,用 $Q,K$ 去计算一个 $thinking$ 对 $thinking,machine$ 的权重,用权重乘以 $thinking,machine$ 的 $V$ 得到加权后的 $thinking,machine$ 的 $V$,最后求和得到针对各个单词的输出 $z$。
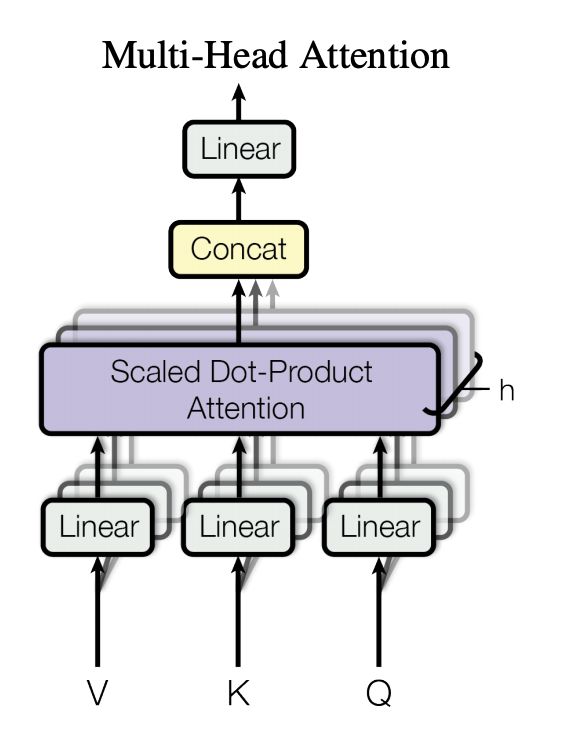
多头注意力机制
论文中表明,将模型分为多个头,形成多个子空间,可以让模型去关注不同方面的信息。上图中Multi-Head Attention 就是将 Scaled Dot-Product Attention 过程做 H 次,再把输出合并起来。
多头注意力机制的公式如下:
$Q_i=QW_i^Q,K_i=KW_i^K,V_i=VW_i^V,i=1,...,8$
$head_i=Attention(Q_i,K_i,V_i),i=1,...,8$
$MultiHead(Q,K,V)=Concact(head_1,...,head_8)W^O$
这里,我们假设 $Q,K,V∈R^{512},W_i^Q,W_i^K,W_i^V∈R^{512\times64},W^O∈R^{512\times512},head_i∈R^{64}$
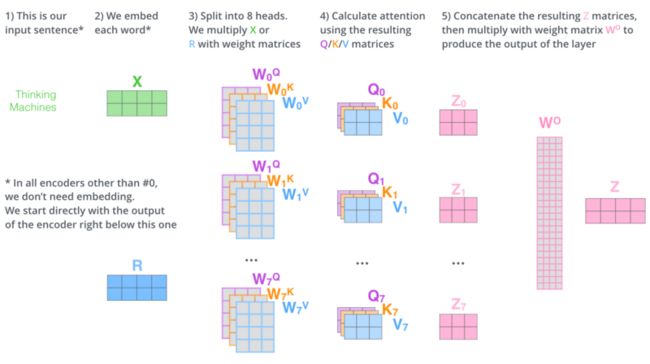
① 输入句子 “tinking machine”② 将句子进行 Tokenize 转换成 Word Embedding X
③ 将 X 切分成 8 份,并与权重 $W_i$ 相乘,构成输入向量 $W_iX$,形成 $Q_i,K_i,V_i,i=1,...,8$
④ 计算 Attention 权重矩阵,$z_i=softmax(Q_iK_i^T/\sqrt{d_k})V_i$,最后将每个 $z_i$ 合并形成 $Z_i$
⑤ 最后将 8 个头的结果 $Z_i,i=1,...8$ 合并 $Z^C=concact(Z_1,...Z_8),i=1,...,8$,点乘权重 $W_O$,形成 $Z=Z^CW_O$
如下面可以看到将 X 有很多的矩阵 $W_0^Q$,
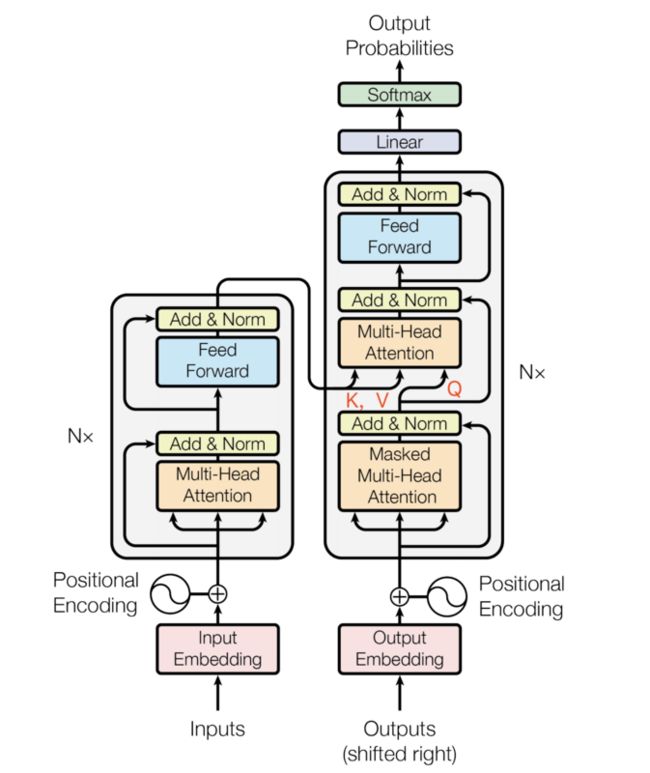
在 Transformer 中,Encoder 的输出会作为 Decoder 的输入,Encoder 的输出是 K,V,Decoder 的上一层输入的 Q。
总结
Transformer 用 自注意力机制的原因在上文有提到过,注意力机制的 Transformer 模型在机器翻译任务中优于 RNN。利用多头注意力扩展了模型集中于不同位置的能力,因此也赋予 Attention 多种子表达方式。