y = a + bx 的目标函数
上一篇文章,我们解释了线性,本文我们回到求解线性回归目标函数的问题上。前面已知,线性回归的目标函数为:
J(a,b)=12m∑mi=1(a+bx(i)−y(i))2
J(a,b) 是一个二元函数。我们要求的是:两个参数 a 和 b 的值。要满足的条件是:a 和 b 取这个值的时候,J(a,b) 的值达到最小。
我们现在就来用之前讲过的算法:梯度下降法,来对其进行求解。
斜率、导数和偏微分
梯度下降法我们前面也讲过步骤,总结起来就是:从任意点开始,在该点对目标函数求导,沿着导数方向(梯度)“走”(下降)一个给定步长,如此循环迭代,直至“走”到导数为0的位置,则达到极小值。
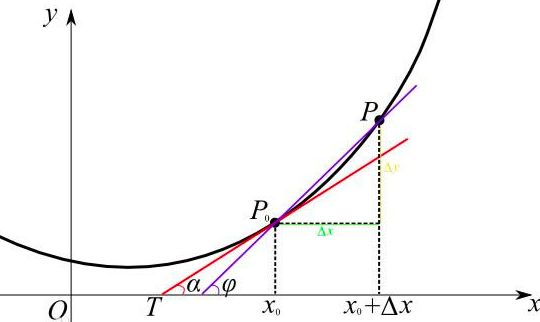
为什么要求导呢?从下图可以看到:曲线表示一个函数,它在一个点处的导数值就是经过这个点的函数曲线切线的斜率。
导数表现的是函数 f(x) 在 x 轴上某一点 x0 处,沿着 x 轴正方向的变化率/变化趋势,记作 f′(x0)。
在 x 轴上某一点处,如果 f′(x0)>0 ,说明 f(x) 的函数值在 x0 点沿 x 轴正方向是趋于增加的;如果 f′(x0)<0,说明 f(x) 的函数值在 x0 点沿 x 轴正方向是趋于减少的。
一元函数在某一点处沿 x 轴正方向的变化率称为导数。但如果是二元或更多元的函数(自变量维度 >=2),则某一点处沿某一维度坐标轴正方向的变化率称为偏导数。
导数/偏导数表现的是变化率,而变化本身,用另一个概念来表示,这个概念就是微分(对应偏导数,二元及以上函数有偏微分)。
(偏)导数是针对函数上的一个点而言的,是一个值。而(偏)微分则是一个函数,其中的每个点表达的是原函数上各点沿着(偏)导数方向的变化。
直观而不严格的来说,(偏)微分就是沿着(偏)导数的方向,产生了一个无穷小的增量。
想想我们的梯度下降算法,我们要做的不就是在一个个点上(沿着导数方向)向前走一小步吗?
当我们求出了一个函数的(偏)微分函数后,将某个变量带入其中,得出的(偏)微分函数对应的函数值,就是原函数在该点处,对该自变量求导的导数值。
所以,只要我们求出了目标函数的(偏)微分函数,那么目标函数自变量值域内每一点的导数值也就都可以求了。
如何求一个函数的(偏)微分函数呢?这个我们只需要记住最基本的求导规则就好,函数(整体,而非在一个点处)求导的结果,就是微分函数了。
本文会用到的仅仅是常用规则中最常用的几条:
- 常数的导数是零:(c)' = 0;
- x 的 n 次幂的导数是 n 倍的 x 的 n-1 次幂:(xn)′=nxn−1;
- 对常数乘以函数求导,结果等于该常数乘以函数的导数:(cf)' = cf';
- 两个函数 f 和 g 的和的导数为:(f+g)' = f' + g';
- 两个函数 f 和 g 的积的导数为:(fg)' = f'g + fg'。
梯度下降求解目标函数
对于 J(a,b) 而言,有两个参数 a 和 b,函数 J 分别对自变量 a 和 b 取偏微分的结果是:
∂J(a,b)∂a=1(m)∑mi=1((a+bx(i))−y(i))
∂J(a,b)∂b=1(m)∑mi=1x(i)((a+bx(i))−y(i))
所以我们要做得是:
Step 1:任意给定 a 和 b 的初值。
a = 0; b = 0;
Step 2:用梯度下降法求解 a 和 b,伪代码如下:
repeatuntilconvergence{a=a−α∂J(a,b)∂a
b=b−α∂J(a,b)∂b
}
当下降的高度小于某个指定的阈值(近似收敛至最优结果),则停止下降。
将上面展开的式子带入上面的代码,就是:
repeatuntilconvergence{
sumA=0
sumB=0
fori=1tom{sumA=sumA+(a+bx(i)−y(i))sumB=sumB+x(i)(a+bx(i)−y(i)) }
a=a−αsumAm
b=b−αsumBm
}
通用线性回归模型的目标函数求解
y = a + bx 是一个线性回归模型,这个没问题。不过,反过来,线性回归模型只能是 y = a + bx 的形式吗?当然不是。
y = a + bx => f(x) = a + bx 实际上是线性回归模型的一个特例——自变量只有一个维度的特例,在这个模型中,自变量 x 是一个一维向量,可写作 [x]。
通用的线性回归模型,是接受 n 维自变量的,也就是说自变量可以写作 [x1,x2,...,xn] 形式。于是,相应的模型函数写出来就是这样的:
f(x1,x2,...,xn)=a+b1x1+b2x2+...+bnxn
这样写参数有点混乱,我们用 θ0 来代替 a, 用 θ1 到 θn 来代替 b1 到 bn,那么写出来就是这样的:
f(1,x1,x2,...,xn)=θ0+θ1x1+θ2x2+...+θnxn
我们设 x0=1, 因此:
f(x0,x1,x2,...,xn)=θ0x0+θ1x1+θ2x2+...+θnxn
那么对应的,n 维自变量的线性回归模型对应的目标函数就是:
J(θ0,θ1,...,θn)=1(2m)∑mi=1(y′(i)−y(i))2=1(2m)∑mi=1(θ0+θ1x(i)1+θ2x(i)2+...+θnx(i)n−y(i))2
再设:
X=[x0,x1,x2,...,xn],Θ=[θ0,θ1,θ2,...,θn]
然后将模型函数简写成:
f(X)=ΘTX
根据习惯,我们在这里将 f(X) 写作 h(X),因此,模型函数就成了:
h(X)=ΘTX
相应的目标函数就是:
J(Θ)=1(2m)∑mi=1(hθ(X(i))−y(i))2
同样应用梯度下降,实现的过程是:
repeatuntilconvergence{Θ=Θ−α∂J(Θ)∂Θ
}
细化为针对 theta_j 的形式就是:
repeatuntilconvergence{
forj=1ton{
sumj=0
fori=1tom{
sumj=sumj+(θ0+θ1x(i)1+θ2x(i)2+...+θnx(i)n−y(i))x(i)j
}
θj=θj−αsumjm
}
}
这就是梯度下降的通用形式。
线性回归的超参数
作为一个线性回归模型,本身的参数是 Θ,在开始训练之前,Θ(无论是多少维),具体的数值都不知道,训练过程就是求解 Θ 中各维度数值的过程。
当我们使用梯度下降求解时,梯度下降算法中的步长参数:α,就是训练线性回归模型的超参数。
训练程序通过梯度下降的计算,自动求出了 Θ 的值。而 α 却是无法求解的,必须手工指定。反之,如果没有指定 α,梯度下降运算则根本无法进行。
- 对于线性回归而言,只要用到梯度下降,就会有步长参数 alpha 这个超参数。
如果训练结果偏差较大,可以尝试调小步长;如果模型质量不错但是训练效率太低,可以适当放大步长;也可以尝试使用动态步长,开始步长较大,随着梯度的缩小,步长同样缩小……
如果训练程序是通过人工指定迭代次数来确定退出条件,则迭代次数也是一个超参数。
如果训练程序以模型结果与真实结果的整体差值小于某一个阈值为退出条件,则这个阈值就是超参数。
在模型类型和训练数据确定的情况下,超参数的设置就成了影响模型最终质量的关键。
而往往一个模型会涉及多个超参数,如何制定策略在最少尝试的情况下让所有超参数设置的结果达到最佳,是一个在实践中非常重要又没有统一方法可以解决的问题。
在实际应用中,能够在调参方面有章法,而不是乱试一气,就有赖于大家对于模型原理和数据的掌握了。
编写线性回归训练/预测程序
如果我们要用代码实现线性回归程序应该怎样做呢?当然,你可以按照上面的描述,自己从头用代码实现一遍。
不过,其实不必。因为我们已经有很多现成的方法库,可以直接调用了。
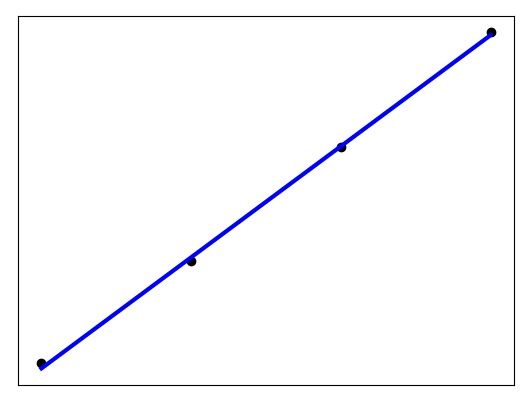
最常见的是 sklearn 库。下面的例子就对应最开始的经验和工资的问题。我们用前 7 个数据作为训练集,后面 4 个作为测试集,来看看结果:
最终结果是这个样子的: