问题76-80参见: https://www.jianshu.com/p/8d4d53f7d18e
81、最小路径和(初级) 2个方向
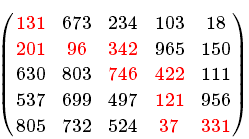
在如下5*5的数字矩阵中,只能向右或向下移动,从左上角到右下角的最小路径和为2427=131+201+96+342+746+422+121+37+331,路径已由红色数字标出:
在文件matrix.txt中包含了一个80*80的矩阵,求该矩阵的左上角到右下角的最小路径和。
Python3解答 动态回归思想参见
import numpy as np
fan=open(r'C:\Users\GWT9\Desktop\p081_matrix.txt')
an =[]
#读取数据
while 1:
x=fan.readline()
if len(x) == 0:
break
du = []
for jjj in list(x.split(',')):
du.append(jjj)
an.append(du)
fan.close()
npan = np.array(an, dtype=int)#转化为np数组形式
#从左上角开始生成斜线坐标直到右下角
weizhi = []
for jj in range(2 * len(npan) - 2):
sonweizhi = []
if jj < len(npan):
for dd in range(jj + 1):
sonweizhi.append([dd, jj - dd])
else:
for dd in range(jj - len(npan) + 1, len(npan)):
sonweizhi.append([dd, jj - dd])
weizhi.append(sonweizhi)
weizhi.append([[len(npan) -1, len(npan) - 1]])
#开始逐斜线计算直到右下角【动态规划思想】
for jj in weizhi[1:]:
for ii in jj:
if ii[0] == 0:
npan[ii[0], ii[1]] += npan[ii[0], ii[1] - 1]
elif ii[1] == 0:
npan[ii[0], ii[1]] += npan[ii[0] -1, ii[1]]
else:
npan[ii[0], ii[1]] += min(npan[ii[0] -1, ii[1]], npan[ii[0], ii[1] - 1])
#输出最终的结果
print(npan[len(npan) -1, len(npan) - 1])
答案:427337
82、最小路径和(中级) 3个方向
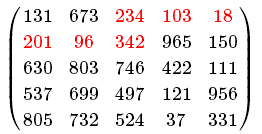
在如下5*5的数字矩阵中,从最左列任意一格出发,只能向右、向上或向下移动,到最右列任意一格结束的最小路径和为994=201+96+342+234+103+18,路径已由红色数字标出:
在文件matrix.txt中包含了一个80*80的矩阵,求该矩阵的最左列到最右列的最小路径和。
Python3解答 动态回归思想参见
import numpy as np
fan=open(r'C:\Users\GWT9\Desktop\p082_matrix.txt')
an =[]
#读取数据
while 1:
x=fan.readline()
if len(x) == 0:
break
du = []
for jjj in list(x.split(',')):
du.append(jjj)
an.append(du)
fan.close()
npan = np.array(an, dtype=int).T#转化为np数组形式转置
copynpan = npan.copy()
#定义组合函数
def combine(nplist, mcode):
comlist = []
for i in range(len(nplist)):
dnum = 0
if i < mcode:
cc = i + 1
while cc < mcode:
dnum += nplist[cc]
cc += 1
comlist.append(dnum)
elif i == mcode:
pass
else:
cc = i - 1
while cc > mcode:
dnum += nplist[cc]
cc -= 1
comlist.append(dnum)
return comlist
for jj in range(1, len(npan)):#开始逐行进行计算【动态规划】
for gg in range(len(npan[jj])):#直接运算
npan[jj, gg] += npan[jj-1, gg]
if jj < len(npan) - 1:
Dcopynpan = copynpan.copy()
for ii in range(len(npan[jj])):#开始比较运算
if ii == 0:
copynpan[jj, ii] += min(copynpan[jj - 1, ii], np.min(npan[jj][1 :] + np.array(combine(Dcopynpan[jj], ii))))#需要比较所有路径
elif ii == len(npan[jj]) - 1:
copynpan[jj, ii] += min(copynpan[jj - 1, ii], np.min(npan[jj][: -1] + np.array(combine(Dcopynpan[jj], ii))))#需要比较所有路径
else:
addlist = np.array(list(npan[jj][: ii]) + list(npan[jj][ii + 1 :]))
copynpan[jj, ii] += min(copynpan[jj - 1, ii], np.min(np.array(combine(Dcopynpan[jj], ii)) + addlist))#需要比较所有路径
npan = copynpan.copy()
else:
print(np.min(npan[-1]))
答案:260324
83、最小路径和(高级) 4个方向
在如下5*5的数字矩阵中,从左上角到右下角任意地向上、向下、向左或向右移动的最小路径和为2297=131+201+96+342+234+103+18+150+111+422+121+37+331,路径已由红色数字标出:
在文件matrix.txt中包含了一个80*80的矩阵,求该矩阵的左上角到右下角的最小路径和。
Python3解答 Dijkstra 算法
import numpy as np
fan=open(r'C:\Users\GWT9\Desktop\p083_matrix.txt')
an =[]
#读取数据
while 1:
x=fan.readline()
if len(x) == 0:
break
du = []
for jjj in list(x.split(',')):
du.append(jjj)
an.append(du)
fan.close()
npan = np.array(an, dtype=int)#转化为np数组形式转置
copynpan = np.array(npan.copy(), dtype = float)
#开始
zuibiaoset = []
for jj in range(len(npan)):
for gg in range(len(npan)):
copynpan[jj, gg] = float('inf')
copynpan[0, 0] = npan[0, 0]
#构建联通字典
liantong = {}
for gg in range(len(npan)):
for hh in range(len(npan)):
dd = [[gg - 1, hh],[gg + 1, hh],[gg, hh - 1],[gg, hh + 1]]
liantong[(gg, hh)] = []
for ff in dd:
if ff[0] >=0 and ff[0] < len(npan) and ff[1] >=0 and ff[1] < len(npan):
liantong[(gg, hh)].append(ff)
#Dijkstra 算法
def Dijkstra(startlist, lidict = liantong, yuanshi = npan, com = copynpan):
start = []
if startlist == []:
return com
else:
for gg in startlist:
fulist = lidict[(gg[0], gg[1])]
for jjj in fulist:
comnumber = com[gg[0], gg[1]] + yuanshi[jjj[0], jjj[1]]
if comnumber < com[jjj[0], jjj[1]]:
com[jjj[0], jjj[1]] = comnumber
start.append(jjj)
return Dijkstra(start)
print(int(Dijkstra([[0, 0]])[-1,-1]))
答案:425185
84、大富翁
答案参见: https://www.jianshu.com/p/758674dfe2cb
85、长方形个数
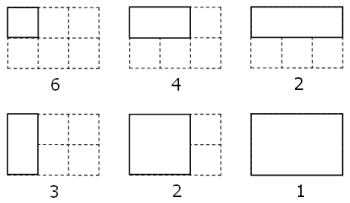
正如下图所示,在一个3*2的长方形网格中含有18=6+4+2+3+2+1个不同大小的长方形:
虽然不存在恰好含有200万个长方形的长方形网格,但有许多长方形网格中含有的长方形数接近200万,求其中最接近这一数的长方形网格的面积。
Python3解答
import numpy as np
i = 1
sanp = np.zeros((3000, 3000))#存储个数
start = 1
num = 100000
sign = 0
while 1:
for j in range(1, start + 1):
sanp[i, j] = sanp[j, i] = sanp[i - 1, j] + sanp[i, j - 1] - sanp[i - 1, j - 1] + i * j#动态规划方法
#计算最小的差值
result = abs(2e6 - sanp[i, j])
if num > result:
num = result
re =[i, j].copy()
if j == 1 and sanp[i, j] > 2e6:
sign = -1
break
if sanp[i, j] > 2e6:
sign = 1
start = j
if sign != 1:
start += 1
if sign == -1:
break
i += 1
print(re[0] * re[1])
答案:2772
持续更新,欢迎讨论,敬请关注!!!