内容分类:认知发展
本文术语:贝叶斯定律、归纳推理(在微信公众号内回复信息,如“贝叶斯定律”,即可查询术语含义)
原文标题:Explaining Constrains Causal Learning in Childhood《解释行为促使儿童的因果学习》
发表杂志: CHILD DEVELOPMENT 8 July 2016
假如你给一个学龄前的孩子买了如下图的一个玩具,并演示给他/她看是如何工作的——向前推动时,玩具在齿轮的带动下会发出音乐。此时你会对孩子说:“好漂亮的小车车哦”、“看,这样会响音乐”、“像妈妈/爸爸这样向前推”,还是,如这篇文章里说的
......
无论成人还是小孩,了解世界的一个重要方法就是归纳总结;而归纳总结最主要的一个任务就是发现隐藏的因果结构,即因果学习。
举个简单的一个例子:开关灯。当你当着一个小孩的面拨动墙上灯源的开关,灯源随之一明一暗。孩子会仰起小脸,看看开关、再转头看看灯。重复几次后,他们的小脑袋里就建立了一个初步的理论——拨动这个地方和电源的明暗有关系。当他们伸出小手,想要自己尝试拨动这个开关并证实了自己的理论的时候,这个因果结构/关系就建立了。
儿童每天面对各种新鲜和千奇百怪的事情,无论大人是否有所引导,因果学习的过程就在儿童的小脑袋里自然而然地发生,他们对世界的认知也随之不断发展。比如,2岁的孩子就对“什么叫解释”有概念了;到4岁,他们就可以提供适合领域的解释;到5岁,他们会在不同的可能的解释中有所选择(比如,他们会倾向于提供更简单的、或能够提供一个目的的解释)。同样是到5岁,儿童已经可以对多个领域的因果关系做出抽象一致的表述,并在不同的推理任务中成功地进行推理思考;这个年纪的儿童还能进行概率推理(即哪种解释可能性更大/更小),并具备了在相关数据的基础上形成新推理的基本能力。
既然因果学习对儿童的认知发展至关重要,那是否有什么简单而富有成效的“小伎俩”可以使之事半功倍呢?虽然一看标题就已天机侧漏,但答案并未完全揭晓。
再继续解密之前,我们必须提起一个人——贝叶斯。学过统计的同学对这个名字一定还有印象,虽然“贝叶斯定律是什么”已经全部交还老师了。我们在这不补统计课,大家别怕!但是心理学角度的”贝叶斯概率推理模型“还是有必要略知一二,因为这是每个人的认知加工过程——即根据不同的信息作推理和决策时,对各种结论出现的概率做出估计。一个5岁的小孩子,让他接受一个有悖于他之前所理解的成因,要比让他接受一个与他之前所理解的相一致的成因困难得多:这个与之前的理解产生矛盾的新证据得更强、更有说服力才行——这个”新证据“和”旧信条“整合的心理过程,就可以用标准贝叶斯模型来表示。成人的世界一样不好搞——有时候在强有力的新证据面前我们不管不顾之前的经验,有时候却又过度依赖之前的经验。
如果把“新证据’和‘旧信条’想象成一架认知天平的两端,那么增添什么样的砝码可以影响这个天平的平衡?本研究把着眼点落在了”对新证据进行解释”这个行为上。有研究显示,解释行为可以促使人把注意力放在不寻常的观察上,从而调整或改变与”新证据“不一致的”旧信条“。另一方面,”解释“会鼓励小朋友用”旧信条“去套”新证据“,然后把”新证据“解释得没那么重要,从而维持住了”旧信条“。
关于“解释或不解释”对推理过程具体会产生的影响,文中提到了之前的两个针对3-6岁小朋友做的对比实验。这两个实验中的被测者被分别提供了一个新玩具/新机器,并让他们解释这个新玩具是怎么工作的,或者这台新机器为什么工作/不工作。
最终两个实验都发现,被鼓励做出解释的测试组比不这么做的控制组更倾向于在玩具/机器的内部性质上找原因(比如齿轮的形状),而非在随意的不相干的感官特征上找原因(如齿轮的颜色)。由此可以看出“解释”不仅可以系统地改变学习到的知识和推论,还能引导学习者倾向于采用那些最有可能支持未来归纳任务的假设。
需特别提出的是,当小朋友给出解释的时候,他们会选择一些看起来不错的“好解释”。评价一个解释是否是个“好解释”的标准之一就是看其解释的数据量有多大,本文称之为“范围”(Scope)。一般来说,这个数据范围越大(比如同时包含新观察到的信息和之前的信息),所做出的推理也越宽越广。
以下内容较专业,非专业读者可跳过,直接阅读“结论部分”☞
在前人经验的基础上,本文作者们就以下三个问题做了进一步探索:
问题一,当小朋友的“旧信条”维持不变时,解释行为会不会让他们支持那些可以解释更多观察内容的假设——即做出一个与“新证据”更相符的解释(实验一)?
问题二,当“新证据”维持不变时,解释行为会不会让他们支持那些与之前的“旧信条”更一致的假设——即做出一个与以前的知识更一致的解释(实验二)?
问题三,当“新证据”和“旧信条”发生矛盾时,解释行为是否会影响小朋友平衡“新证据”和“旧信条”之间的关系呢(实验三)?
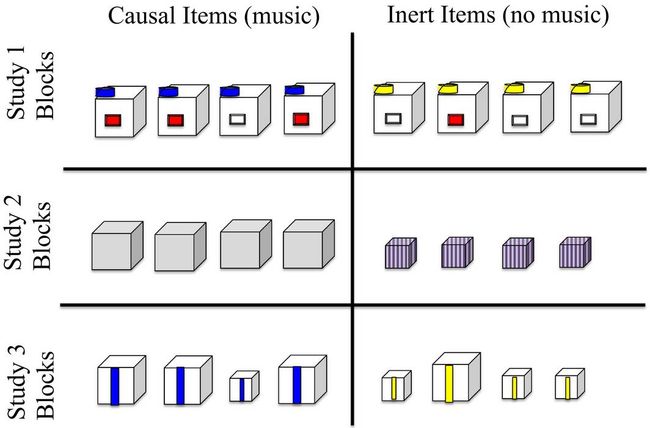
这三个问题读起来有点绕口,实际上整个实验设计得虽周全也绝对够复杂(点击文末“阅读原文”查看原版论文)。我们在这里就简要介绍一下整个实验的原理就好——整个实验分为两大部分:培训环节和测试环节。测试者把不同大小和形状的木块(如下图)放在一个机器上,有些木块会让机器响音乐,有些则不能。
在培训环节,5岁的小朋友通过观察习得了一定的规律——即哪些颜色或大小的木块可以让机器工作,哪些则不能。这些规律印在小朋友的脑子里,成为了“旧信条”。测试组的小朋友在每一次培训环节结束后,会被问道:“为什么这个木块(不)会使我的机器响音乐呢?”;而控制组的小朋友在每一次培训环节结束后,会被问:“当我把这个木块放在机器上的时候,发生了什么?它响音乐了吗?”
在接下来的测试环节,两块不同的木块会同时被遮掩起来,仅展示/告知其部分特征;测试者还会改变了一些游戏规则,如:在保持旧规律的基础上增加不同特征的木块(即“旧信条”遇到“新证据”),或创造一个不同于之前的让机器发声的游戏规则(即“旧信条”遇到“新信条”)。所有的小朋友在每次观察到机器的反应后,都被要求在刚才观察的两块木块中进行选择判断:哪个(不)会让机器响音乐?小朋友们的回答按一定的规则被标上分数,0或1。接下来的统计数据分析则是根据这些分数来进行的。
|结论部分|
小小学习者每次观察到一个新的现象,这个现象可能和之前观察到的相符或不相符。那么,当他们在分别被问道“为什么?”和“发生了什么?”时,不同的引导问题会引起他们对这个现象不同的理解并影响到后来的判断吗?更具体来讲,当他们遇到不同情况时,会把新观察到的现象或以前的经验考虑进来吗?
本实验探索的基本问题就是——解释行为是否可以增加解释性假设的信息包含量。最终结果基本证实了最初的假设——解释行为会鼓励小小学习者支持那些涵盖更大信息量的“好”假设。三个实验的具体结果可分别概括如下:
实验一:“解释”可以让学习者对新出现的信息(新证据)更敏感;
实验二:“解释”还可以引导学习者做出和以前的知识更相符的假设;
实验三:当新观察到的现象和以前的知识不相符时,无论学习者最后做出的解释正确与否,“解释”会促使他们更全面地考虑和权衡新旧信息。
|编后语|
回到开篇时的那个问题。当你给孩子演示一个包含因果关系的玩具时,如那个彩色的齿轮推车,你希望他/她看到的是什么?是玩具的外部特征(如齿轮的大小或颜色),还是齿轮的内部性质(如卡齿形状)?如果你希望孩子不只是简单地被玩具多彩的颜色或新颖的样式所吸引,而注意到齿轮-音乐这个隐藏着的因果关系,你只需要引导地问孩子:“你觉得这辆小车为什么会发出音乐呢?”
处在同样的学习环境下,接受同样的信息,学习的效果却可能完全不同。比如像这个实验里说明的那样:只是成人在引导时发问的问题从“发生了什么?”转变为“为什么会发生?”,小小学习者所领悟到的知识会更深、所做的推理会更广。正如标题所泄露的天机——
“来,解释一下”,认知发展就这么搞上去了。
原创编译:
微信公众号“常青蒙馆”