Learning to rank(简写 LTR、L2R) 也叫排序学习,指的是机器学习中任何用于排序的技术。
为什么要用LTR
传统的检索模型靠人工拟合排序公式,并通过不断的实验确定最佳的参数组合,以此来形成相关性打分。这种方式非常简单高效,应该范围也很广,比如简单的博客排序、论坛的QA排序等.但是也同时存在较大的问题:
- 手动调参工作量太大
- 可能会过拟合
- 如果模型参数很多,手动调参的可用性就很低了~
LTR与此思路不同,最合理的排序公式由机器学习算法来确定,而人则需要给机器学习提供训练数据,他的优势有:
- 可以自动调节参数
- 可以融合多方面观点的(evidences)的数据
- 避免过拟合(通过正则项)
LTR基本框架
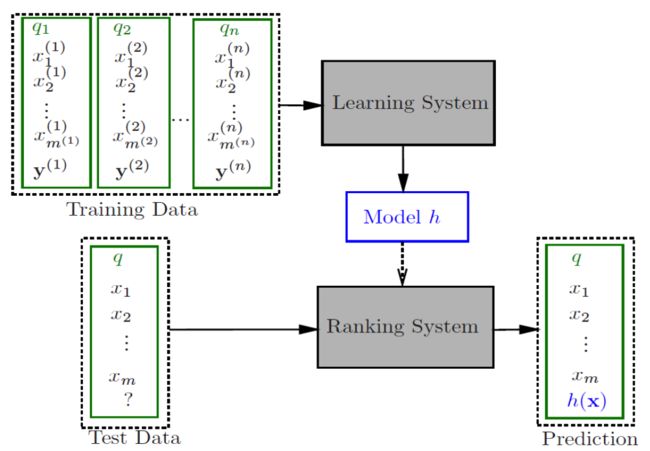
LTR的核心还是机器学习,只是目标不仅仅是简单的分类或者回归了,最主要的是产出文档的排序结果,它通常的工作框架如下:
所描述的步骤为:训练数据获取->特征提取->模型训练->测试数据预测->效果评估
训练数据的获取
人工标注
人工标注的数据主要有以下几大类型:
-
单点标注
对于每个查询文档打上绝对标签
二元标注:相关 vs 不相关
-
五级标注:完美(Perfect),出色(Excellent),好(Good),一般(Fair),差(Bad) ,一般后面两档属于不相关
好处:标注的量少O(n)
坏处:难标。。。不好统一
-
两两标注
-
对于一个查询
Query,要标注文档d1比文档d2是否更加相关 (q,d1)≻(q,d2)?好处:标注起来比较方便
坏处:标注量大 估计得有O(n^2)
-
-
列表标注
-
对于一个查询
Query,将人工理想的排序整个儿标好好处: 相对于上面两种,标的效果会很好
坏处: 这个工作量也太大了…-_-||
-
日志抽取
当搜索引擎搭建起来之后用户的点击数据就变得非常好使。
比如,结果ABC分别位于123位,B比A位置低,但却得到了更多的点击,那么B的相关性可能好于A.
这种点击数据隐含了Query到文档的相关性好坏。所以一般会使用点击倒置的高低位结果作为训练数据.
但是他也是存在问题的:
- 用户总是习惯于从上到下浏览搜索结果
- 用户点击有比较大的噪声
- 一般头查询(
head query)才存在用户点击
这里的日志提取可以参考Learning to rank在淘宝的应用,干货!!!
特征提取
检索系统会使用一系列特征来表示一次查询,通过模型之后最终决定文档的排序顺序,这里用q来表示查询,d表示查询的文档,occur−term共现的词,则提取的特征主要有以下三大类:
- occur−term特征
- 共现在查询中的出现次数、比率等
- occur−term的特征
- 共现在文档中的出现次数、比率等
- 共现词与文档的相关性特征:
BM25系列
- 自身特征
-
PageRank值 -
Spam信息 -
Quality质量分 - 行为分,
ctr,停留时间,二跳率等..
-
模型训练
LTR的模型主要有单文档方法(Pointwise Approach)、文档对方法(Pairwise Approach)和列表方法(Listwise Approach)三大类,下面是实现他们的各种算法:
Pointwise Approach
Pointwise的处理对象是单独的一篇文档,将文档转换为特征向量之后,机器学习模型根据从训练数据中学习到的分类或者回归函数对文档打分,打分的结果就是搜索的结果.
其实就是将文档排序转为了文档的回归、分类和有序分类问题,其函数的框架为:
L(F(X),y)=∑i=1nl(f(xi)−yi)
输入:
- 单个文档查询对:(xi,yi)
- 完全忽略上下文的关系
- 将标注转为数字,比如
Perfect->5, Excellent->4, Good->3, Fair->2, Bad->1
输出:
- 排序函数,对于给定查询文档对,能够计算出得分(score)
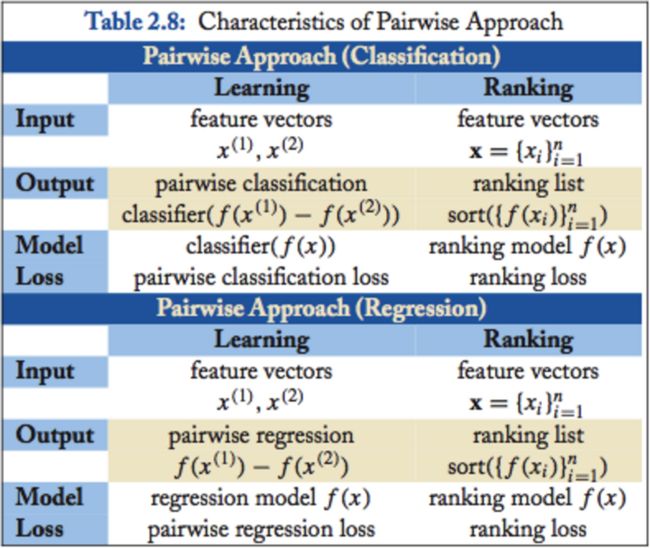
关于Pointwise下的三个分支,这张图解释的很好:
其主要区别就是loss function不同,也就是最后的结果目标不一样:
-
Classification:输入的是5档类别(作为离散),最后通过分类模型输测试数据的各个档位档位的概率,然后进行加权成一个实数值 -
Regression:输入的是5档或者2档(作为连续),最后通过回归模型输出测试数据的一个相关性实数(就是回归) -
Ordinal Classification:输入的档位是有序的,比如像上面一样输入5档,但是他们的权重不一样,可能权重最高档位的分类(二分类),再进行次高档位的分词,依次下去(McRank的paper有讲)
实现Pointwise方法的主要算法有:
- Classification
- Discriminative model for IR (SIGIR 2004)
- McRank (NIPS 2007)
- Regression
- Least Square Retrieval Function (TOIS 1989)
- Regression Tree for Ordinal Class Prediction (Fundamenta Informaticae, 2000)
- Subset Ranking using Regression (COLT 2006)
- Ordinal Classification
- Pranking (NIPS 2002)
- OAP-BPM (EMCL 2003)
- Ranking with Large Margin Principles (NIPS 2002)
- Constraint Ordinal Regression (ICML 2005)
优点:
- 速度快,复杂度低.
缺点:
- 效果一般
- 没有考虑到文档之间的相对关系
- 忽略了文档相关度与查询的关联,比如
Top Query排在后面的相关性比Tial Query排在前面的都要高,导致训练样本不一致
Pairwise Approach
对于搜索任务来说,系统接收到用户查询后,返回相关文档列表,所以问题的关键是确定文档之间的先后相对顺序关系,
而Pairwise则将重点转向对文档关系是否合理的判断.
Pairwise主要是讲排序问题转为了文档对顺序的判断
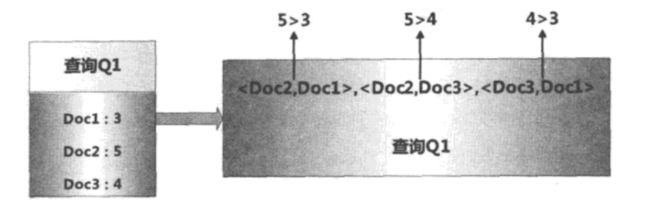
以下图为例:
对于查询
Q1进行人工标注之后,
Doc2=5的分数最高,其次是
Doc3为4分,最差的是
Doc1为3分,将此转为相对关系之后有:
Doc2>Doc1、Doc2>Doc3、Doc3>Doc1,而根据这个顺序关系逆向也可以得到相关性的排序顺序,所以排序问题可以很自然的转为任意两个文档关系的判断,而任意两个文档顺序的判断就称为了一个很熟悉的分类问题.
Pairwise的函数框架为:
L(F(x),y)=∑i=1n−1∑j=i+1n(sign(yi−yj),f(xi)−f(xj))
输入:
- 同一查询的一对文档(xi,xj,sign(yi−yj))
- 标注两个文档的相对关系,如果文档xi比xj更加相关,则sign(yi−yj))=1
- 分布保留同一查询下的文档间关系
输出:
- 排序函数给出文档对的计算得分
关于Pairwise最终的算分,其实分类和回归都可以实现:
实现Pairwise Approach方法的主要算法有:
- Learning to Retrieve Information (SCC 1995)
- Learning to Order Things (NIPS 1998)
- Ranking SVM (ICANN 1999)
- RankBoost (JMLR 2003)
- LDM (SIGIR 2005)
- RankNet (ICML 2005)
- Frank (SIGIR 2007)
- MHR(SIGIR 2007)
- GBRank (SIGIR 2007)
- QBRank (NIPS 2007)
- MPRank (ICML 2007)
- IRSVM (SIGIR 2006)
- LambdaRank (NIPS 2006)
虽然Pairwise方法对Pointwise方法做了改进,但是也明显存在两个问题:
- 只考虑了两个文档的先后顺序,没有考虑文档出现在搜索列表中的位置
- 不同的查询,其相关文档数量差异很大,转换为文档对之后,有的查询可能有几百对文档,有的可能只有几十个,最终对机器学习的效果评价造成困难
Listwise Approach
与Pointwise和Pairwise不同,Listwise是将一个查询对应的所有搜索结果列表作为一个训练实例,因此也称为文档列方法.
文档列方法根据K个训练实例训练得到最优的评分函数,对于一个新的查询,函数F对每一个文档进行打分,之后按照得分顺序高低排序,就是对应的搜索结果.
Listwise主要有两类:
-
Measure specific:损失函数与评估指标相关,比如:L(F(x),y)=exp(−NDCG) -
Non-measure specific:损失函数与评估指标不是显示相关,考虑了信息检索中的一些独特性质
实现Listwise的算法主要有:
- Measure-specific
- AdaRank (SIGIR 2007)
- SVM-MAP (SIGIR 2007)
- SoftRank (LR4IR 2007)
- RankGP (LR4IR 2007)
- LambdaMART (inf.retr 2010)
- Non-measure specific
- ListNet (ICML 2007)
- ListMLE (ICML 2008)
- BoltzRank (ICML 2009)
实验表明 一般
Listwise要好于前两种排序算法,但是其复杂度是在太高了
方法对比
| pointwise | pairwise | listwise | |
|---|---|---|---|
| 输入信息的完整度 | 不完全 | 部分完全 | 完全 |
| 输入 | (x,y) | (x1,x2,y) | (x1,x2…xn,π) |
| 输出 | f(x) | f(x) | f(x) |
| 样本复杂度 | O(n) | O(n^2) | O(n!) |
| 表现 | 差 | 中 | 好 |
评估指标
MAP
MAP(Mean Average Precision)表示文档在排序中的平均精度均值,是用于衡量个query查询见过的平均精度值AP,
系统检索出来的相关文档越靠前(rank 越高),MAP就可能越高。如果系统没有返回相关文档,则准确率默认为0。
所以对于计算AP的值就是关键了,MAP对文档只分为两档:相关与不相关,则AP表示为
AP=∑ni:relvancePi/Rin
其中Pi表示所有召回文档中相关文档的相对次序,Ri表示所有被召回的相关文档中在所有文档中的次序
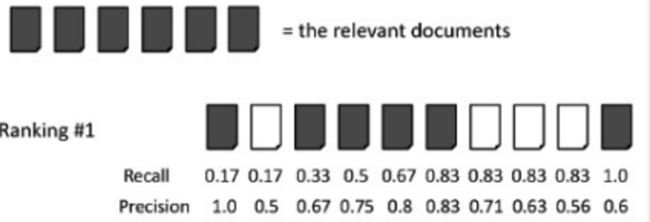
比如在某个query得到的排序中:
则他的相对顺序的表格为:
| O | X | O | O | O | O | X | X | X | O | |
|---|---|---|---|---|---|---|---|---|---|---|
| 相关文档次序 | 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 所有召回文档次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Precision | 1/1 | 2/3 | 3/4 | 4/5 | 5/6 | 6/10 |
最终计算的AP=(1/1+2/3+3/4+4/5+5/6+6/10)/6=0.78
NDCG
NDCG表示表示归一化折损累积增益,主要是衡量实际相关性越高的文档排在越前面,它的全称是Normalized Discounted Cumulative Gain,也正好代表了4个部分的含义:
-
Gain:表示增益,一般相关性越高,增益值也是越大
Gi=2yi−1
> 其中yi表示文档相关性档位,一般档位越高,相关性越大
-
Discounted:一般认为排序位置 带来的权重不同,所以会有一个折损因子
DGi=2yi−1log(1+i)
> 其中i为文档的排序位置,从1开始
-
Cumulative:表示在一次query查询中所有的增益累加
DCG=∑i=1n2yi−1log(1+i)
-
Normalized:为归一化,因为在不同的查询中可能DCG的值波动较大,这里计算各个query最理想的排序的DCG值作为归一化因子,也称为IDCG
NDCG=1IDCG⋅∑i=1n2yi−1log(1+i)
NDCG的可使用性更加广泛了,但是还是存在以下三点限制:
-
NDCG并没有对不相关文档进行惩罚 -
NDCG对一些缺失的完成结果也没有进行惩罚 -
NDCG也不是用档位大家都相等的情况(比如每页里面的doc相关性都是差不多的)
公开数据集
- http://research.microsoft.com/en-us/um/beijing/projects/letor/
- http://research.microsoft.com/en-us/projects/mslr/
- http://webscope.sandbox.yahoo.com/
总结
在玩搜索引擎时敲定特征分的权重是非常疼的一件事儿,而LTR正好帮你定分,LTR的三种实现方法其实各有优劣:
- 难点主要在训练样本的构建(人工或者挖日志),另外就是训练复杂
- 虽说
Listwise效果最好,但是天下武功唯快不破,看看这篇文章http://www.cnblogs.com/zjgtan/p/3652689.html体验下 - 在工业界用的比较多的应该还是
Pairwise,因为他构建训练样本相对方便,并且复杂度也还可以,所以Rank SVM就很火啊_
参考
- 《这就是搜索引擎:核心技术详解》 . 第五章
- Learning to Rank小结
- 机器学习及排序学习基础
- Learning to Rank for Information Retrieval
- https://en.wikipedia.org/wiki/Discounted_cumulative_gain
- https://www.kaggle.com/wiki/MeanAveragePrecision