MPT,全称Merkle Patricia Trie,以太坊中用来存储用户账户的状态及其变更、交易信息、交易的收据信息。看其全称便大概知道MPT融合了MerkleTree,Trie,Patricia Trie这三种数据结构的有点,从而最大限度地快速实现查找功能并节省空间。
前尘旧事
Trie
Trie,又称为字典树或者前缀树 (prefix tree),属于查找树的一种。它与平衡二叉树的主要不同点包括:
- 每个节点数据所携带的 key 不会存储在 Trie 的节点中,而是通过该节点在整个树形结构里位置来体现(下图中标注出完整的单词,只是为了演示Trie的原理);
- 同一个父节点的子节点,共享该父节点的 key 作为它们各自 key 的前缀,因此根节点 key 为空;
- 待存储的数据只存于叶子节点和部分内部节点中,非叶子节点帮助形成叶子节点 key 的前缀。
通俗地讲,以Trie存储英文单词为例,只需要把每个单词按字母拆分然后在树上进行查找,找深度和单词长度相同为止。eg:
Patricia Trie
就以上面的Trie来看,对于节点5这个只有一个子节点的节点来说,其实没有必要衍生出节点9来构造存储inn,我们完全可以把这种只有一个子节点的节点和其子节点合并为一个节点来节省存储空间。
这就是基于Trie改进后的Patricia Trie,又被称为 RadixTree 或紧凑前缀树 (compact prefix tree),是一种空间使用率经过优化的 Trie。
Merkle Tree
MerkleTree,通常也被称作Hash Tree,顾名思义,就是存储hash值的一棵树。之前在公链开发中有涉及到Merkle Tree理解和代码实现,在此不再赘述。
MPT
概念理解
MPT 是 Ethereum 自定义的 Trie 型数据结构。以上面存储英文单词的Trie为例,一个Trie实际上就是一个26叉树。而MPT在以太坊里是用来检索字节数据的,因此这里的MPT实际上是一个16叉树,分别代表0x0 - 0xf。
MPT节点一共有四个类型:
- 空节点(NULL)
- 分支节点(branch node):17个分 ,包含16个bytes(0x0-0xf)以及1个value
- 扩展节点(extension node):只有1个子结点
- 叶子节点(leaf node):没有子节点,包含1个value
针对MPT树的理解,可以借助他山之石,毕竟站在巨人的肩膀上会看得更远。我们这里主要目的是研读以太坊源码,对概念的理解就不再展开叙述。
关于MPT,wiki里也给出了一个简单的示例,可以去看看。
废话少说撸代码
基本操作
接下来就直捣黄龙,来看看以太坊源码是如何实现MPT的。
首先,来看MPT树几种节点的定义(./trie/node.go)。
// MPT几种节点结构
type (
// 分支节点,它的结构体现了原生trie的设计特点
fullNode struct {
// 17个子节点,其中16个为0x0-0xf;第17个子节点存放数据
Children [17]node // Actual trie node data to encode/decode (needs custom encoder)
// 缓存节点的Hash值,同时标记dirty值来决定节点是否必须写入数据库
flags nodeFlag
}
// 扩展节点和叶子节点,它的结构体现了PatriciaTrie的设计特点
// 区别在于扩展节点的value指向下一个节点的hash值(hashNode);叶子节点的value是数据的RLP编码(valueNode)
shortNode struct {
Key []byte
Val node
flags nodeFlag
}
//节点哈希,用于实现节点的折叠(参考MerkleTree设计特点)
hashNode []byte
//存储数据
valueNode []byte
)
接着来看看MPT树几种重要的更新操作:新建,插入,查找等。首先看新建:./trie/trie.go
// New creates a trie with an existing root node from db.
//
// If root is the zero hash or the sha3 hash of an empty string, the
// trie is initially empty and does not require a database. Otherwise,
// New will panic if db is nil and returns a MissingNodeError if root does
// not exist in the database. Accessing the trie loads nodes from db on demand.
func New(root common.Hash, db *Database) (*Trie, error) {
if db == nil {
panic("trie.New called without a database")
}
trie := &Trie{
db: db,
originalRoot: root,
}
// 如果根哈希不为空,说明是从数据库加载一个已经存在的MPT树
if root != (common.Hash{}) && root != emptyRoot {
rootnode, err := trie.resolveHash(root[:], nil)
if err != nil {
return nil, err
}
trie.root = rootnode
}
//否则,直接返回的是新建的MPT树
return trie, nil
}
接着,来看MPT树的插入操作。
/*
insert MPT树节点的插入操作
node 当前的节点
prefix 当前已处理完的key(节点共有的前缀)
key 当前未处理的key(完整key = prefix + key)
value 当前插入的值
bool 返回函数是否改变了MPT树
node 执行插入后的MPT树根节点
*/
func (t *Trie) insert(n node, prefix, key []byte, value node) (bool, node, error) {
if len(key) == 0 {
if v, ok := n.(valueNode); ok {
return !bytes.Equal(v, value.(valueNode)), value, nil
}
return true, value, nil
}
switch n := n.(type) {
case *shortNode:
// 如果是叶子节点,首先计算共有前缀
matchlen := prefixLen(key, n.Key)
// If the whole key matches, keep this short node as is
// and only update the value.
// 1.1如果共有前缀和当前的key一样,说明节点已经存在 只更新节点的value即可
if matchlen == len(n.Key) {
dirty, nn, err := t.insert(n.Val, append(prefix, key[:matchlen]...), key[matchlen:], value)
if !dirty || err != nil {
return false, n, err
}
return true, &shortNode{n.Key, nn, t.newFlag()}, nil
}
// Otherwise branch out at the index where they differ.
// 1.2构造形成一个分支节点(fullNode)
branch := &fullNode{flags: t.newFlag()}
var err error
// 1.3将原来的节点拆作新的后缀shortNode插入
_, branch.Children[n.Key[matchlen]], err = t.insert(nil, append(prefix, n.Key[:matchlen+1]...), n.Key[matchlen+1:], n.Val)
if err != nil {
return false, nil, err
}
// 1.4将新节点作为shortNode插入
_, branch.Children[key[matchlen]], err = t.insert(nil, append(prefix, key[:matchlen+1]...), key[matchlen+1:], value)
if err != nil {
return false, nil, err
}
// Replace this shortNode with the branch if it occurs at index 0.
// 1.5 如果没有共有的前缀,则新建的分支节点为根节点
if matchlen == 0 {
return true, branch, nil
}
// Otherwise, replace it with a short node leading up to the branch.
// 1.6 如果有共有的前缀,则拆分原节点产生前缀叶子节点为根节点
return true, &shortNode{key[:matchlen], branch, t.newFlag()}, nil
case *fullNode:
// 2 若果是分支节点,则直接将新数据插入作为子节点
dirty, nn, err := t.insert(n.Children[key[0]], append(prefix, key[0]), key[1:], value)
if !dirty || err != nil {
return false, n, err
}
n = n.copy()
n.flags = t.newFlag()
n.Children[key[0]] = nn
return true, n, nil
case nil:
// 3 空节点,直接返回该值得叶子节点作为根节点
return true, &shortNode{key, value, t.newFlag()}, nil
case hashNode:
// We've hit a part of the trie that isn't loaded yet. Load
// the node and insert into it. This leaves all child nodes on
// the path to the value in the trie.
// 4.1哈希节点 表示当前节点还未加载到内存中,首先需要调用resolveHash从数据库中加载节点
rn, err := t.resolveHash(n, prefix)
if err != nil {
return false, nil, err
}
// 4.2然后在该节点后插入新节点
dirty, nn, err := t.insert(rn, prefix, key, value)
if !dirty || err != nil {
return false, rn, err
}
return true, nn, nil
default:
panic(fmt.Sprintf("%T: invalid node: %v", n, n))
}
}
不难看出,MPT树节点的插入操作是一个不断递归调用insert函数的过程。从根节点开始不断向下找,直到找到可以插入的节点为止。虽然代码我作了详细的注释,我们还是通过一个简单来理解下这个插入过程。
- a.在空节点的MPT插入第1个节点node1(b621411,40),由于当前MPT树节点为空,这里走的是代码里的3操作。此时直接返回leafNode1作为根节点,因为当前MPT只有一个叶子节点
| leafNode1 | b621411 | 40 |
|---|
- b.0接着插入第2个节点node2(a543918,100),此时当前的节点为叶子节点node1,这里走的是代码1.2操作。首先需要构造一个分支节点branchNode1:
| 0 | 1 | 2 | 3 | ... | a | b | ... | f | value |
|---|
- b.1然后将原来的节点node1插入到branchNode1(代码1.3操作);并把新的节点插入到branchNode1后(代码1.4操作)。这是递归调用insert函数进入下一步时的当前节点便成为了branchNode1,相当于将问题转换为代码2.
b.2 上面已经知道node1,node2并没有共同前缀。因此,此时代码里走的是1.5将brenchNode1返回作为根节点
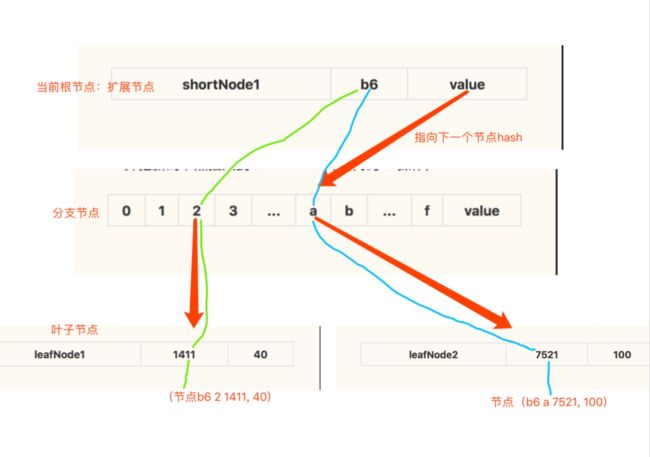
c.0若此时的node2为(b6a7521, 100),比较node1,node2发现两个节点有共同的前缀b6,此时需要构造一个扩展节点shortNode1(节点value指向下一个节点hash)存储两个节点的共同前缀,然后再构造一个brenchNode2来连接node1,node2
- c.1 此时由于拥有共同节点,所以要返回的根节点为原节点拆分的存储共同前缀的节点(代码1.6)
同样,节点的delete操作与insert逻辑互逆,也是通过不断地递归调用delete函数直到找到应该删除的节点,然后要看情况合并删除节点后只有一个子节点的父节点。
// delete returns the new root of the trie with key deleted.
// It reduces the trie to minimal form by simplifying
// nodes on the way up after deleting recursively.
// 删除节点
func (t *Trie) delete(n node, prefix, key []byte) (bool, node, error) {
switch n := n.(type) {
case *shortNode:
// 如果是叶子节点或扩展节点,首先获取与当前节点的共同前缀
matchlen := prefixLen(key, n.Key)
// 删除节点不存在,不需要删除 MPT树不变
if matchlen < len(n.Key) {
return false, n, nil // don't replace n on mismatch
}
// 删除节点为当前共有节点(即根节点),删除后MPT为空
if matchlen == len(key) {
return true, nil, nil // remove n entirely for whole matches
}
// The key is longer than n.Key. Remove the remaining suffix
// from the subtrie. Child can never be nil here since the
// subtrie must contain at least two other values with keys
// longer than n.Key.
// key > n.key,从key中删除剩余的后缀
// 子节点这里不会为空,因为至少有2个拥有key值得子节点 取其子节点
dirty, child, err := t.delete(n.Val, append(prefix, key[:len(n.Key)]...), key[len(n.Key):])
if !dirty || err != nil {
return false, n, err
}
switch child := child.(type) {
case *shortNode:
// Deleting from the subtrie reduced it to another
// short node. Merge the nodes to avoid creating a
// shortNode{..., shortNode{...}}. Use concat (which
// always creates a new slice) instead of append to
// avoid modifying n.Key since it might be shared with
// other nodes.
return true, &shortNode{concat(n.Key, child.Key...), child.Val, t.newFlag()}, nil
default:
return true, &shortNode{n.Key, child, t.newFlag()}, nil
}
case *fullNode:
dirty, nn, err := t.delete(n.Children[key[0]], append(prefix, key[0]), key[1:])
if !dirty || err != nil {
return false, n, err
}
n = n.copy()
n.flags = t.newFlag()
n.Children[key[0]] = nn
// Check how many non-nil entries are left after deleting and
// reduce the full node to a short node if only one entry is
// left. Since n must've contained at least two children
// before deletion (otherwise it would not be a full node) n
// can never be reduced to nil.
//
// When the loop is done, pos contains the index of the single
// value that is left in n or -2 if n contains at least two
// values.
pos := -1
for i, cld := range n.Children {
if cld != nil {
if pos == -1 {
pos = i
} else {
pos = -2
break
}
}
}
if pos >= 0 {
if pos != 16 {
// If the remaining entry is a short node, it replaces
// n and its key gets the missing nibble tacked to the
// front. This avoids creating an invalid
// shortNode{..., shortNode{...}}. Since the entry
// might not be loaded yet, resolve it just for this
// check.
cnode, err := t.resolve(n.Children[pos], prefix)
if err != nil {
return false, nil, err
}
if cnode, ok := cnode.(*shortNode); ok {
k := append([]byte{byte(pos)}, cnode.Key...)
return true, &shortNode{k, cnode.Val, t.newFlag()}, nil
}
}
// Otherwise, n is replaced by a one-nibble short node
// containing the child.
return true, &shortNode{[]byte{byte(pos)}, n.Children[pos], t.newFlag()}, nil
}
// n still contains at least two values and cannot be reduced.
return true, n, nil
case valueNode:
return true, nil, nil
case nil:
return false, nil, nil
case hashNode:
// We've hit a part of the trie that isn't loaded yet. Load
// the node and delete from it. This leaves all child nodes on
// the path to the value in the trie.
rn, err := t.resolveHash(n, prefix)
if err != nil {
return false, nil, err
}
dirty, nn, err := t.delete(rn, prefix, key)
if !dirty || err != nil {
return false, rn, err
}
return true, nn, nil
default:
panic(fmt.Sprintf("%T: invalid node: %v (%v)", n, n, key))
}
}
那怎么获取存储在MPT上的数据呢?继续看代码:
// Get returns the value for key stored in the trie.
// The value bytes must not be modified by the caller.
// 获取MPT上存储的数据
func (t *Trie) Get(key []byte) []byte {
res, err := t.TryGet(key)
if err != nil {
log.Error(fmt.Sprintf("Unhandled trie error: %v", err))
}
return res
}
// TryGet returns the value for key stored in the trie.
// The value bytes must not be modified by the caller.
// If a node was not found in the database, a MissingNodeError is returned.
// 获取MPT上存储的数据
func (t *Trie) TryGet(key []byte) ([]byte, error) {
key = keybytesToHex(key)
value, newroot, didResolve, err := t.tryGet(t.root, key, 0)
if err == nil && didResolve {
t.root = newroot
}
return value, err
}
// 遍历MPT节点
func (t *Trie) tryGet(origNode node, key []byte, pos int) (value []byte, newnode node, didResolve bool, err error) {
switch n := (origNode).(type) {
case nil:
return nil, nil, false, nil
case valueNode:
return n, n, false, nil
case *shortNode:
// key不存在
if len(key)-pos < len(n.Key) || !bytes.Equal(n.Key, key[pos:pos+len(n.Key)]) {
// key not found in trie
return nil, n, false, nil
}
// 扩展节点继续递归找到叶子节点
value, newnode, didResolve, err = t.tryGet(n.Val, key, pos+len(n.Key))
if err == nil && didResolve {
n = n.copy()
n.Val = newnode
n.flags.gen = t.cachegen
}
return value, n, didResolve, err
case *fullNode:
// 递归寻找叶子节点
value, newnode, didResolve, err = t.tryGet(n.Children[key[pos]], key, pos+1)
if err == nil && didResolve {
n = n.copy()
n.flags.gen = t.cachegen
n.Children[key[pos]] = newnode
}
return value, n, didResolve, err
case hashNode:
// hash节点,先从数据库里加载出当前节点再继续寻找
child, err := t.resolveHash(n, key[:pos])
if err != nil {
return nil, n, true, err
}
value, newnode, _, err := t.tryGet(child, key, pos)
return value, newnode, true, err
default:
panic(fmt.Sprintf("%T: invalid node: %v", origNode, origNode))
}
}
MPT的序列化
Compat编码
序列化主要是用来把内存中的数据放到数据库中,反序列化则反之。以太坊 MPT的序列化主要用到了Compat编码和RLP编码。
RLP编码前面已经介绍过,这里简单看一下Compat编码。
Compat编码,又叫hex prefix编码(HP),它是基于hex编码。所以首先要明白Hex编码是怎么一回事。
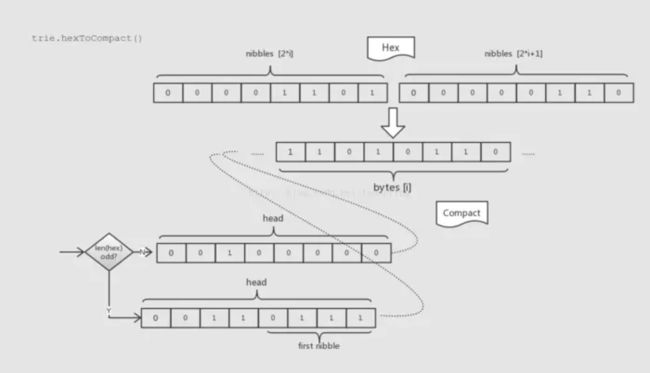
Hex编码:当[key, value]数据插入MPT时,这里的key必须经过特殊编码以保证能以16进制形式按位进入fullNode.Children[]。由于Children数组最多容纳16个字节点,所以以太坊这里定义了Hex编码方式将1bytes的字符大小限制在4bit(16进制)以内。trie给出的Hex编码方式如下:
从图上可以看出,Hex编码主要有两步:
- 1.将1个byte的高低4bit分别放到2个byte里,形成新的byte[]
- 2.在新byte[]后再追加1个byte来标记当前byte[]为Hex格式
Compat编码:主要作用用来将Hex格式的字符串恢复到keybytes格式,同时加入当前Compat格式的标记位,还要考虑奇偶不同长度Hex字符串下避免引入多余的bytes。
从图上可以看出,Compat编码主要有两步:
1.将Hex格式的尾部标记byte去掉,然后将每2nibble的数据合并到1个byte
2.判断Hex编码长度,如果输入 Hex 格式字符串有效长度为偶数,偶数标志位0010,这样新增1byte来放置compat标志位就为00100000;反之将Hex字符串第一个nibble放置在标记位低4bit,加上奇数标志位0011的compat标志位就为0011xxxx。
大概了解了原理之后就可以看源码了(./trie/encoding.go)
// Trie keys are dealt with in three distinct encodings:
//
// KEYBYTES encoding contains the actual key and nothing else. This encoding is the
// input to most API functions.
//
// HEX encoding contains one byte for each nibble of the key and an optional trailing
// 'terminator' byte of value 0x10 which indicates whether or not the node at the key
// contains a value. Hex key encoding is used for nodes loaded in memory because it's
// convenient to access.
//
// COMPACT encoding is defined by the Ethereum Yellow Paper (it's called "hex prefix
// encoding" there) and contains the bytes of the key and a flag. The high nibble of the
// first byte contains the flag; the lowest bit encoding the oddness of the length and
// the second-lowest encoding whether the node at the key is a value node. The low nibble
// of the first byte is zero in the case of an even number of nibbles and the first nibble
// in the case of an odd number. All remaining nibbles (now an even number) fit properly
// into the remaining bytes. Compact encoding is used for nodes stored on disk.
// Hex编码串转化为Compact编码
func hexToCompact(hex []byte) []byte {
// 如果最后一位是16,terminator为1,否则为0
terminator := byte(0)
// 包含terminator的节点为叶子节点
if hasTerm(hex) {
terminator = 1
// 1.0将Hex格式的尾部标记byte去掉
hex = hex[:len(hex)-1]
}
// 定义Compat字节数组
buf := make([]byte, len(hex)/2+1)
// 标志位默认
buf[0] = terminator << 5 // the flag byte
if len(hex)&1 == 1 {
// 如果Hex长度为奇数,修改标志位为odd flag
buf[0] |= 1 << 4 // odd flag
// 然后把第1个nibble放入buf[0]低四位
buf[0] |= hex[0] // first nibble is contained in the first byte
hex = hex[1:]
}
// 1.1然后将每2nibble的数据合并到1个byte
decodeNibbles(hex, buf[1:])
return buf
}
// Compact编码转化为Hex编码串
func compactToHex(compact []byte) []byte {
base := keybytesToHex(compact)
// delete terminator flag
/*这里base[0]有4中情况
00000000 扩展节点偶数位
00000001 扩展节点奇数位
00000010 叶子节点偶数位
00000011 叶子节点偶数位
*/
if base[0] < 2 {
// 如果是扩展节点,去除最后一位
base = base[:len(base)-1]
}
// apply odd flag
// 如果是偶数位chop=2,否则chop=1
chop := 2 - base[0]&1
//去除compact标志位。偶数位去除2个字节,奇数位去除1个字节(因为奇数位的低四位放的是nibble数据)
return base[chop:]
}
// 将key字符串进行Hex编码
func keybytesToHex(str []byte) []byte {
l := len(str)*2 + 1
//将一个keybyte转化成两个字节
var nibbles = make([]byte, l)
for i, b := range str {
nibbles[i*2] = b / 16
nibbles[i*2+1] = b % 16
}
//末尾加入Hex标志位16 00010000
nibbles[l-1] = 16
return nibbles
}
// hexToKeybytes turns hex nibbles into key bytes.
// This can only be used for keys of even length.
// 将hex编码解码转为key字符串
func hexToKeybytes(hex []byte) []byte {
if hasTerm(hex) {
hex = hex[:len(hex)-1]
}
if len(hex)&1 != 0 {
panic("can't convert hex key of odd length")
}
key := make([]byte, len(hex)/2)
decodeNibbles(hex, key)
return key
}
func decodeNibbles(nibbles []byte, bytes []byte) {
for bi, ni := 0, 0; ni < len(nibbles); bi, ni = bi+1, ni+2 {
bytes[bi] = nibbles[ni]<<4 | nibbles[ni+1]
}
}
// prefixLen returns the length of the common prefix of a and b.
func prefixLen(a, b []byte) int {
var i, length = 0, len(a)
if len(b) < length {
length = len(b)
}
for ; i < length; i++ {
if a[i] != b[i] {
break
}
}
return i
}
// hasTerm returns whether a hex key has the terminator flag.
func hasTerm(s []byte) bool {
return len(s) > 0 && s[len(s)-1] == 16
}
这里涉及到一个叶子节点的判断hasTerm,使用compact编码的规格:
| hex char | bits | node | path length |
|---|---|---|---|
| 0 | 0000 | extension | even(偶数) |
| 1 | 0001 | extension | even(偶数) |
| 2 | 0010 | leaf(terminator) | odd(奇数) |
| 3 | 0011 | leaf | odd(奇数) |
MPT序列化
了解了MPT编码方式之后,来看看涉及MPT编码存储的一个简单流程。我们在trie_test.go里的insert测试函数来看看MPT编码存储的逻辑。
func TestInsert(t *testing.T) {
// 1.创建一个空的MPT树
trie := newEmpty()
updateString(trie, "doe", "reindeer")
updateString(trie, "dog", "puppy")
updateString(trie, "dogglesworth", "cat")
exp := common.HexToHash("8aad789dff2f538bca5d8ea56e8abe10f4c7ba3a5dea95fea4cd6e7c3a1168d3")
root := trie.Hash()
if root != exp {
t.Errorf("exp %x got %x", exp, root)
}
trie = newEmpty()
updateString(trie, "A", "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa")
exp = common.HexToHash("d23786fb4a010da3ce639d66d5e904a11dbc02746d1ce25029e53290cabf28ab")
// 2.调用Commit函数进行序列化
root, err := trie.Commit(nil)
if err != nil {
t.Fatalf("commit error: %v", err)
}
if root != exp {
t.Errorf("exp %x got %x", exp, root)
}
}
...
// Commit writes all nodes to the trie's memory database, tracking the internal
// and external (for account tries) references.
// 序列化MPT树,并将所有节点数据存储到数据库中
func (t *Trie) Commit(onleaf LeafCallback) (root common.Hash, err error) {
if t.db == nil {
panic("commit called on trie with nil database")
}
// 3.折叠MPT节点的实现
hash, cached, err := t.hashRoot(t.db, onleaf)
if err != nil {
return common.Hash{}, err
}
t.root = cached
t.cachegen++
return common.BytesToHash(hash.(hashNode)), nil
}
// 折叠MPT节点的实现
func (t *Trie) hashRoot(db *Database, onleaf LeafCallback) (node, node, error) {
if t.root == nil {
return hashNode(emptyRoot.Bytes()), nil, nil
}
h := newHasher(t.cachegen, t.cachelimit, onleaf)
defer returnHasherToPool(h)
// 4.将节点进行哈希
return h.hash(t.root, db, true)
}
继续深入到hash函数里来分析:
// hash collapses a node down into a hash node, also returning a copy of the
// original node initialized with the computed hash to replace the original one.
// 将节点向下折叠为hash node,同时返回用计算出的散列初始化的原始节点的副本以替换原始节点。
/*
node MPT根节点
db 存储的数据库
force true 当节点的RLP字节长度小于32也对节点的RLP进行hash计算
根节点调用为true以保证对根节点进行哈希计算
return:
node 入参n经过哈希折叠后的hashNode
node hashNode被赋值了的同时未被哈希折叠的入参n
*/
func (h *hasher) hash(n node, db *Database, force bool) (node, node, error) {
// If we're not storing the node, just hashing, use available cached data
if hash, dirty := n.cache(); hash != nil {
if db == nil {
return hash, n, nil
}
// 移除节点 当trie.cachegen-node.cachegen > cachelimit
if n.canUnload(h.cachegen, h.cachelimit) {
// Unload the node from cache. All of its subnodes will have a lower or equal
// cache generation number.
cacheUnloadCounter.Inc(1)
return hash, hash, nil
}
if !dirty {
return hash, n, nil
}
}
// Trie not processed yet or needs storage, walk the children
// 将所有子节点替换成他们的Hash
collapsed, cached, err := h.hashChildren(n, db)
if err != nil {
return hashNode{}, n, err
}
// 将所有节点都换算完hash的hashNode存入数据库
hashed, err := h.store(collapsed, db, force)
if err != nil {
return hashNode{}, n, err
}
// Cache the hash of the node for later reuse and remove
// the dirty flag in commit mode. It's fine to assign these values directly
// without copying the node first because hashChildren copies it.
cachedHash, _ := hashed.(hashNode)
switch cn := cached.(type) {
case *shortNode:
cn.flags.hash = cachedHash
if db != nil {
cn.flags.dirty = false
}
case *fullNode:
cn.flags.hash = cachedHash
if db != nil {
cn.flags.dirty = false
}
}
return hashed, cached, nil
}
// hashChildren replaces the children of a node with their hashes if the encoded
// size of the child is larger than a hash, returning the collapsed node as well
// as a replacement for the original node with the child hashes cached in.
// 把所有的子节点替换成他们的hash,可以看到cache变量接管了原来的Trie树的完整结构
// collapsed变量把子节点替换成子节点的hash值。
func (h *hasher) hashChildren(original node, db *Database) (node, node, error) {
var err error
switch n := original.(type) {
case *shortNode:
// Hash the short node's child, caching the newly hashed subtree
// 当前节点为叶子节点或扩展节点,将collapsed.Key从Hex编码转换为Compat编码
collapsed, cached := n.copy(), n.copy()
collapsed.Key = hexToCompact(n.Key)
cached.Key = common.CopyBytes(n.Key)
//循环调用hash算法将collapsed中子节点全换成子节点的hash值
if _, ok := n.Val.(valueNode); !ok {
collapsed.Val, cached.Val, err = h.hash(n.Val, db, false)
if err != nil {
return original, original, err
}
}
return collapsed, cached, nil
case *fullNode:
// Hash the full node's children, caching the newly hashed subtrees
collapsed, cached := n.copy(), n.copy()
// 分支节点,遍历将子节点全换成子节点的hash值
for i := 0; i < 16; i++ {
if n.Children[i] != nil {
collapsed.Children[i], cached.Children[i], err = h.hash(n.Children[i], db, false)
if err != nil {
return original, original, err
}
}
}
cached.Children[16] = n.Children[16]
return collapsed, cached, nil
default:
// Value and hash nodes don't have children so they're left as were
// 没有子节点,直接返回
return n, original, nil
}
}
// store hashes the node n and if we have a storage layer specified, it writes
// the key/value pair to it and tracks any node->child references as well as any
// node->external trie references.
// MPT节点存储
func (h *hasher) store(n node, db *Database, force bool) (node, error) {
// Don't store hashes or empty nodes.
if _, isHash := n.(hashNode); n == nil || isHash {
return n, nil
}
// Generate the RLP encoding of the node
h.tmp.Reset()
// 调用rlp.Encode方法对这个节点进行编码
if err := rlp.Encode(&h.tmp, n); err != nil {
panic("encode error: " + err.Error())
}
// 如果编码后的值 < 32 并且没有要求强制保存(根节点),直接存储在父节点中
if len(h.tmp) < 32 && !force {
return n, nil // Nodes smaller than 32 bytes are stored inside their parent
}
// Larger nodes are replaced by their hash and stored in the database.
// 如果编码后的值 > 32 存储到数据库中
hash, _ := n.cache()
if hash == nil {
hash = h.makeHashNode(h.tmp)
}
if db != nil {
// We are pooling the trie nodes into an intermediate memory cache
hash := common.BytesToHash(hash)
db.lock.Lock()
// 数据库存储的key为node经过RLP编码后的hash值
db.insert(hash, h.tmp, n)
db.lock.Unlock()
// Track external references from account->storage trie
if h.onleaf != nil {
switch n := n.(type) {
case *shortNode:
if child, ok := n.Val.(valueNode); ok {
h.onleaf(child, hash)
}
case *fullNode:
for i := 0; i < 16; i++ {
if child, ok := n.Children[i].(valueNode); ok {
h.onleaf(child, hash)
}
}
}
}
}
return hash, nil
}
这里的大概逻辑是这样的:
1.调用hash函数作了三个操作:一是保留了原有的树形结构到cached,二是计算了原有树形结构的hash并把其存到hashed里,三是在有子节点的节点调用了hashChildren函数来递归地将所有子节点变为他们的哈希值。
2.hashChildren用于遍历每一个节点,其中又嵌套调用了hash函数来计算节点的哈希值,hashChildren与hash函数相互调用正好遍历了整个MPT树结构。
3.store函数对节点做RLP编码,并将节点存储到数据库中
MPT反序列化
其实在之前看insert函数源码时就涉及到了MPT反序列化。当时遇到当前节点为hashNode时,需要调用t.resolveHash函数从数据库取出当前节点来进行操作,这个过程便是MPT节点的反序列化。
// 根据hashNode取出对应的节点
func (t *Trie) resolveHash(n hashNode, prefix []byte) (node, error) {
cacheMissCounter.Inc(1)
hash := common.BytesToHash(n)
// 通过hash解析出node的RLP值
if node := t.db.node(hash, t.cachegen); node != nil {
return node, nil
}
return nil, &MissingNodeError{NodeHash: hash, Path: prefix}
}
看来真正的解码操作在database类里,循着线索继续深入。
// node retrieves a cached trie node from memory, or returns nil if none can be
// found in the memory cache.
// 从内存中检索缓存的MPT节点,如果在内存缓存中找不到任何节点,则返回nil。
func (db *Database) node(hash common.Hash, cachegen uint16) node {
// Retrieve the node from cache if available
db.lock.RLock()
node := db.nodes[hash]
db.lock.RUnlock()
if node != nil {
return node.obj(hash, cachegen)
}
// Content unavailable in memory, attempt to retrieve from disk
enc, err := db.diskdb.Get(hash[:])
if err != nil || enc == nil {
return nil
}
// 真正根据hash接触node的函数
return mustDecodeNode(hash[:], enc, cachegen)
}
...
func mustDecodeNode(hash, buf []byte, cachegen uint16) node {
n, err := decodeNode(hash, buf, cachegen)
if err != nil {
panic(fmt.Sprintf("node %x: %v", hash, err))
}
return n
}
...
// decodeNode parses the RLP encoding of a trie node.
// 解析MPT节点的RLP编码。
func decodeNode(hash, buf []byte, cachegen uint16) (node, error) {
//空节点
if len(buf) == 0 {
return nil, io.ErrUnexpectedEOF
}
elems, _, err := rlp.SplitList(buf)
if err != nil {
return nil, fmt.Errorf("decode error: %v", err)
}
switch c, _ := rlp.CountValues(elems); c {
// 这里根据rlpList的长度来判断节点类型,2为shortNode,17的话是fullNode
case 2:
n, err := decodeShort(hash, elems, cachegen)
return n, wrapError(err, "short")
case 17:
n, err := decodeFull(hash, elems, cachegen)
return n, wrapError(err, "full")
default:
return nil, fmt.Errorf("invalid number of list elements: %v", c)
}
}
到这里,就根据分辨出的节点类型来解码。decodeShort和decodeFull逻辑大致相同,我们以decodeShort为例来深入了解下解码逻辑。
// 针对shortNode的解码方式
func decodeShort(hash, elems []byte, cachegen uint16) (node, error) {
// kbuf -- compact key;rest -- 节点的value
kbuf, rest, err := rlp.SplitString(elems)
if err != nil {
return nil, err
}
flag := nodeFlag{hash: hash, gen: cachegen}
// 1.将key从conmpact编码转换为Hex字符串
key := compactToHex(kbuf)
// 2.根据是否包含终结符号(16--00010000)来判断是否为叶子节点
if hasTerm(key) {
// value node
// 包含16,是叶子节点
val, _, err := rlp.SplitString(rest)
if err != nil {
return nil, fmt.Errorf("invalid value node: %v", err)
}
return &shortNode{key, append(valueNode{}, val...), flag}, nil
}
// 3.解析剩下的节点
r, _, err := decodeRef(rest, cachegen)
if err != nil {
return nil, wrapError(err, "val")
}
return &shortNode{key, r, flag}, nil
}
...
// 解析剩余节点
func decodeRef(buf []byte, cachegen uint16) (node, []byte, error) {
kind, val, rest, err := rlp.Split(buf)
if err != nil {
return nil, buf, err
}
switch {
case kind == rlp.List:
// 'embedded' node reference. The encoding must be smaller
// than a hash in order to be valid.
// 根据RLP编码规则 len(buf) - len(rest)为类型加内容的长度
if size := len(buf) - len(rest); size > hashLen {
err := fmt.Errorf("oversized embedded node (size is %d bytes, want size < %d)", size, hashLen)
return nil, buf, err
}
// 递归调用decodeNode解析函数
n, err := decodeNode(nil, buf, cachegen)
return n, rest, err
case kind == rlp.String && len(val) == 0:
// empty node
return nil, rest, nil
case kind == rlp.String && len(val) == 32:
// 数据类型为hash值,构造一个hashNode返回
return append(hashNode{}, val...), rest, nil
default:
return nil, nil, fmt.Errorf("invalid RLP string size %d (want 0 or 32)", len(val))
}
}
MPT数据结构
MPT的东西源码里还真不少,以至于都忘记来看看其数据结构了。
// Trie is a Merkle Patricia Trie.
// The zero value is an empty trie with no database.
// Use New to create a trie that sits on top of a database.
//
// Trie is not safe for concurrent use.
// MPT
type Trie struct {
// 保存节点的数据库
db *Database
// MPT根节点
root node
// MPT根哈希
originalRoot common.Hash
// Cache generation values.
// cachegen increases by one with each commit operation.
// new nodes are tagged with the current generation and unloaded
// when their generation is older than than cachegen-cachelimit.
// cachegen -- Cache generation values,缓存生成值。每次执行commit操作
// cachegen都会自增1
// cachelimit 缓存限制值
// 当trie.cachegen-node.cachegen > cachelimit 移除节点
cachegen, cachelimit uint16
}
加密的MPT
为了避免使用太长的key导致访问时间太久,以太坊用security_trie对上述trie作了一个封装,使得最后所有的key都转换成keccak256算法计算的hash值。同时在数据库里映射存储了对应的原有key。
type SecureTrie struct {
// MPT树
trie Trie
// 缓存key经过keccak256后的哈希值
hashKeyBuf [common.HashLength]byte
// 映射hash值和原有key的关系
secKeyCache map[string][]byte
// self
secKeyCacheOwner *SecureTrie // Pointer to self, replace the key cache on mismatch
}
与MPT类似,SecureTrie也有get,delete,commit等操作,这里就不再赘述。
说起来,以太坊有关MPT的实现源码还真不少。还有很多细节还没有去看,作为理解以太坊MPT,这些已经足够了。
以太坊四棵树
以太坊的每一个区块头里都包含着三颗树的根节点:
-
- transactionsRoot,交易树
-
- receiptsRoot,收据树
-
- stateRoot,状态树
还有一颗树在以太坊账户account里,每一个account都包含nonce,balance,storageRoot,codeHash四个子项,其中便有第四棵树的根节点:
-
- storageRoot,存储树,它是所有合约数据存储的地方
MPT是以太坊特有的自己构造的树结构。今天,已经将MPT的基本机制和源码实现看完了。
更多以太坊源码解析请移驾全球最大同性交友网,觉得有用记得给个小star哦
.
.
.
.
互联网颠覆世界,区块链颠覆互联网!
--------------------------------------------------20180926 01:19