上一章 散列（一） 主要介绍了散列的基本概念以及冲突解决方法--分离链表法。这一章主要介绍解决冲突的另一种方法---开放定址法。
开放定址法：尝试另外一些单元，直到找出空的单元为止。
- 线性探测法：当产生冲突时，它将寻找下一个空闲地址放入。
- 平方探测法：使用 f(i) = i 2 的方法来解决冲突，并且保证如果表有一半为空，并且表的大小为素数，那么我们保证总能够插入一个新的元素。
双散列：使用如下探测方法：
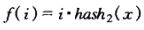double_hashing.png
线性探测法：
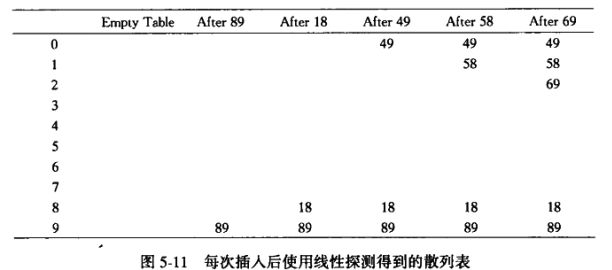
在线性探测法中，函数f是i的线性函数，典型的情形为f(i) = i 。 这相当于探测逐个单元(必要时可以回绕)以查找出一个空单元。
线性探测.png
如上图，我们逐个插入关键字{89，18，49，58，69}。第一个冲突发生在插入49关键字，它和89产生了冲突(因为49%10=9且89%10=9)，因此，49被推入下一个空闲位置，即位置0 ( 注意这里是可以回绕的) ,紧接着插入58，58和18冲突了，则找下一个空闲位置，找到位置1.对于69的冲突也是一样的。
我们发现即使表相对较空，还是会发生一些占据的单元集中在一些块区，这种现象我们成为一次聚集。
也就是说，散列在区块中的任何关键字都需要多次试选单元才能解决冲突，然后将关键字添加进去。
实验证明，当装填因子(散列表中元素个数与该表大小的比)在0 ~ 0.5之间所需探测的次数时较小的，考虑到探测次数和rehash的消耗，我们一般采用0.5作为装填因子会达到比较好的效果。
线性探测.png
平方探测法
- 平方探测法是消除线性探测中一次聚集问题的解决冲突的方法。平方探测就是冲突函数为二次的探测方法。
- 对于线性探测，让散列表中填满元素并不是一个好主意，因为此时表的性能在下降。而对于平方探测方法情况甚至更糟：一旦表被填充了一半，当表的大小不是素数时甚至在表被填充一半之前，就不能保证一次找到空的单元了。这是因为最多有表的一半作为解决冲突的备选位置。
- 定理：** 如果使用平方探测，且表的大小是素数，那么当表至少有一半是空的时候，总能够插入一个新的元素**。
- 在探测散列表中的删除操作，我们不能直接执行，因为相应的单元可能已经引起过冲突，被转移到其他地方了。
a. 定义一个类用来标记每个位置的值以及其是否处于活动状态(即是否存在值)
/**
* 定义一个类用来标记每个位置的情况
* @param
*/
private static class HashEntry{
//当前位置的元素值
public AnyType element;
//当前位置是否为活动状态，默认为活动状态，但若删除后，会设置其为非活动状态
public boolean isActive;
public HashEntry(AnyType e){
this(e, true);
}
public HashEntry(AnyType e, boolean b){
element = e;
isActive = b;
}
}
b. 定义所需变量：
//默认表的大小
private static final int DEFAULT_TABLE_SIZE = 11;
//存储表
private HashEntry [] array;
//当前表的大小
private int currentSize;
c. 进行初始化操作：
//无参数构造函数
public QuadraticProbingHashTable(){
this(DEFAULT_TABLE_SIZE);
}
//有参数构造函数
public QuadraticProbingHashTable(int size){
allocateArray(size);
makeEmpty();
}
//清空表
public void makeEmpty(){
currentSize = 0;
for (int i = 0; i < array.length; i ++){
array[i] = null;
}
}
//初始化表
private void allocateArray(int size){
array = new HashEntry[nextPrime(size)];
}
c. 解决冲突位置：
/**
* 寻找空闲位置，以解决冲突
* @param x
* @return
*/
private int findPos(AnyType x){
//定义偏移量
int offset = 1;
//获取到hash位置
int currentPos = myHash(x);
//若hash位置中存在元素,并且当前元素不等于传入的元素
while (array[currentPos] != null && !array[currentPos].element.equals(x)){
//进行偏移
currentPos += offset;
//改变偏移量
offset += 2;
//考虑到溢出情况
if (currentPos >= array.length){
currentPos -= array.length;
}
}
return currentPos;
}
d. 插入操作：
//插入元素
public void insert(AnyType x){
//获取到空闲位置
int currentPos = findPos(x);
//若该位置为活动状态，则返回，表示该位置已经存在元素
//这种情况，实际上表示该位置上已经存在了该元素，那么不必重复插入
if (isActive(currentPos)){
return;
}
//否则，插入该元素
array[currentPos] = new HashEntry(x);
//判断表的大小，超过一半，则进行rehash
if (++ currentSize > array.length / 2){
rehash();
}
}
//判断当前位置是否为活动状态
private boolean isActive(int currentPos){
return array[currentPos] != null && array[currentPos].isActive;
}
e. 删除操作：
public void remove(AnyType x){
//找到位置
int currentPos = findPos(x);
//若该位置为活动状态，则进行删除操作
if (isActive(currentPos)){
//令该位置为非活动状态即可
array[currentPos].isActive = false;
currentSize --;
}
}
f. 查询操作：
public boolean contains(AnyType x){
int currentPos = findPos(x);
//返回该位置是否为活动状态
return isActive(currentPos);
}
g. rehash操作：
private void rehash(){
HashEntry [] oldArray = array;
//扩充表的大小
allocateArray(nextPrime(2 * oldArray.length));
currentSize = 0;
//将旧表的数据添加到新表中
for (int i = 0; i < oldArray.length; i ++){
if (oldArray[i] != null && oldArray[i].isActive){
insert(oldArray[i].element);
}
}
}
完整代码：
public class QuadraticProbingHashTable {
//无参数构造函数
public QuadraticProbingHashTable(){
this(DEFAULT_TABLE_SIZE);
}
//有参数构造函数
public QuadraticProbingHashTable(int size){
allocateArray(size);
makeEmpty();
}
//清空表
public void makeEmpty(){
currentSize = 0;
for (int i = 0; i < array.length; i ++){
array[i] = null;
}
}
public boolean contains(AnyType x){
int currentPos = findPos(x);
//返回该位置是否为活动状态
return isActive(currentPos);
}
//插入元素
public void insert(AnyType x){
//获取到空闲位置
int currentPos = findPos(x);
//若该位置为活动状态，则返回，表示该位置已经存在元素
//这种情况，实际上表示该位置上已经存在了该元素，那么不必重复插入
if (isActive(currentPos)){
return;
}
//否则，插入该元素
array[currentPos] = new HashEntry(x);
//判断表的大小，超过一半，则进行rehash
if (++ currentSize > array.length / 2){
rehash();
}
}
public void remove(AnyType x){
//找到位置
int currentPos = findPos(x);
//若该位置为活动状态，则进行删除操作
if (isActive(currentPos)){
//令该位置为非活动状态即可
array[currentPos].isActive = false;
currentSize --;
}
}
/**
* 定义一个类用来标记每个位置的情况
* @param
*/
private static class HashEntry{
//当前位置的元素值
public AnyType element;
//当前位置是否为活动状态，默认为活动状态，但若删除后，会设置其为非活动状态
public boolean isActive;
public HashEntry(AnyType e){
this(e, true);
}
public HashEntry(AnyType e, boolean b){
element = e;
isActive = b;
}
}
//默认表的大小
private static final int DEFAULT_TABLE_SIZE = 11;
//存储表
private HashEntry [] array;
//当前表的大小
private int currentSize;
//初始化表
private void allocateArray(int size){
array = new HashEntry[nextPrime(size)];
}
//判断当前位置是否为活动状态
private boolean isActive(int currentPos){
return array[currentPos] != null && array[currentPos].isActive;
}
/**
* 寻找空闲位置，以解决冲突
* @param x
* @return
*/
private int findPos(AnyType x){
//定义偏移量
int offset = 1;
//获取到hash位置
int currentPos = myHash(x);
//若hash位置中存在元素,并且当前元素不等于传入的元素
while (array[currentPos] != null && !array[currentPos].element.equals(x)){
//进行偏移
currentPos += offset;
//改变偏移量
offset += 2;
//考虑到溢出情况
if (currentPos >= array.length){
currentPos -= array.length;
}
}
return currentPos;
}
private void rehash(){
HashEntry [] oldArray = array;
//扩充表的大小
allocateArray(nextPrime(2 * oldArray.length));
currentSize = 0;
//将旧表的数据添加到新表中
for (int i = 0; i < oldArray.length; i ++){
if (oldArray[i] != null && oldArray[i].isActive){
insert(oldArray[i].element);
}
}
}
//根据值获取到其对应的hash位置
private int myHash(AnyType x){
int hashVal = x.hashCode();
hashVal %= array.length;
if (hashVal < 0){
hashVal += array.length;
}
return hashVal;
}
//返回下一个素数
private static int nextPrime(int n){
while (!isPrime(n)){
n ++;
}
return n;
}
//判断是否为素数
private static boolean isPrime(int n){
for (int i = 2; i <= Math.sqrt(n); i ++){
if (n % i == 0 && n != 2){
return false;
}
}
return true;
}
}