用python的pulp库解决线性规划问题

本文会介绍怎么用python解决线性规划问题，为什么要用python而不是matlab和lingo呢？因为matlab的函数写法不太符合正常的思维方式，编起来很复杂。而lingo虽然编写容易，但报错不详细，一旦有错很难查出来。而python就没有这些问题。

关于python的语法就不再介绍了，主要介绍pulp库的用法。

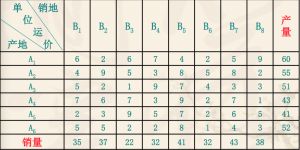
以此题为例：计算6个生产点8个销售点的最小费用运输问题。产销单位运价如下表。

先建模，很容易得到以下模型：

现在开始编程：

引入头文件是必须的：

#-*- coding: UTF-8 -*-

importnumpyasnp

frompulpimport*

step1先新建一个问题，随便取名为prob：

prob = LpProblem("test1", LpMinimize)

step2然后定义变量为x，每个x代表了对应的A点卖到B点的数量：

foriinrange(1, 49, 1):

exec('x%s= LpVariable("x%s", 0, None, LpInteger,[])'%(i,i))

x = [[x1,x2,x3,x4,x5,x6,x7,x8],[x9,x10,x11,x12,x13,x14,x15,x16],

[x17,x18,x19,x20,x21,x22,x23,x24],[x25,x26,x27,x28,x29,x30,x31,x32],

[x33,x34,x35,x36,x37,x38,x39,x40],[x41,x42,x43,x44,x45,x46,x47,x48]]

对于LpVariable函数包含的参数，一次为变量名，变量值的最小值，变量值的最大值，变量类型。

这里LpInteger表示变量的类型是int型，根据题目的需要还可以改成LpContinuous(实数型)和LpBinary(二值型，即0或1)。

step3开始写入数据：

cost = np.array([[6,2,6,7,4,2,9,5],[4,9,5,3,8,5,8,2],[5,2,1,9,7,4,3,3],

[7,6,7,3,9,2,7,1],[2,3,9,5,7,2,6,5],[5,5,2,2,8,1,4,3]])

capacity = np.array([60,55,51,43,41,52])

demand = np.array([35,37,22,32,41,32,43,38])

产地的产量为capacity，销地的销量为demand，单位运价为cost

step4设定目标函数：

result = 0

foriinrange(0, 6):

forjinrange(0, 8):

result += x[i][j]*cost[i][j]

prob += result, "obj"

是以result最小为目标的，如果要求结果最大为目标的题目可在result前面加上负号。

step5还要设置约束：

产量的约束：

foriinrange(1,7,1):#设置产量的约束

exec('prob += sum(x[%s]) <= capacity[%s]' % (i - 1, i - 1))

销量的约束：

foriinrange( 1 , 9 , 1):#设置销量的约束

z=0

forjinrange( 1 , 7 , 1):

z+=x[j-1][i-1]

exec('prob += z >= demand[%s]'%(i-1))

step6需要编写的部分就已经完成了，只需要输出结果就行了

# Solve the problem using the default solver

prob.solve()

# Print the status of the solved LP

print ( "Status:", LpStatus[prob.status] )

# Print the value of the variables at the optimum

forvinprob.variables():

print (v.name, "=", v.varValue)

# Print the value of the objective

print ( "objective=", value(prob.objective) )

输出的内容分别是计算状态（optimal时就说明结果正常），变量值，和目标函数值。

这题就做完啦～

最后把代码汇总一下：

#-*- coding: UTF-8 -*-

import numpy as np

from pulp import *

# A new LP problem

prob = LpProblem("test1", LpMinimize)

cost = np.array([[6,2,6,7,4,2,9,5],[4,9,5,3,8,5,8,2],[5,2,1,9,7,4,3,3],

[7,6,7,3,9,2,7,1],[2,3,9,5,7,2,6,5],[5,5,2,2,8,1,4,3]])

capacity = np.array([60,55,51,43,41,52])

demand = np.array([35,37,22,32,41,32,43,38])

# Variables

for i in range(1, 49, 1):

exec('x%s= LpVariable("x%s", 0, None, LpInteger,[])'%(i,i))

x = [[x1,x2,x3,x4,x5,x6,x7,x8],[x9,x10,x11,x12,x13,x14,x15,x16],

[x17,x18,x19,x20,x21,x22,x23,x24],[x25,x26,x27,x28,x29,x30,x31,x32],

[x33,x34,x35,x36,x37,x38,x39,x40],[x41,x42,x43,x44,x45,x46,x47,x48]]

# Objective

result = 0

for i in range(0, 6):

for j in range(0, 8):

result += x[i][j]*cost[i][j]

prob += result, "obj"

# (the name at the end is facultative)

# Constraints

# for i in range(1,7,1):#先对y赋值

for i in range(1,7,1):#设置产量的约束