第二章我们来学习椭圆曲线。后面我们会把椭圆曲线和有限域结合起来,得到我们强大的武器Elliptic curve cryptography。
就像有限域一样,如果你之前没见过,可能会被椭圆曲线吓退啦。但是,实际上没有那么困难哦。大多数我们所需的知识都已经学过了。这章,我们将探索这些曲线是什么,并且能够用来做什么。
定义:
椭圆曲线就跟其他方程式一样啦,一边是y,一边是x。如下:
果然一样吧!就像以前我们学的线性方程一样,m是斜率,b是截距:
二次三次也来了!
这些图像都还是很熟悉的。
椭圆曲线也没有什么不同~只是左边是y^2,这使得两个正负的y值对应的是同一个x,所以图像是关于x轴对称的。
椭圆曲线没三次函数那么陡峭,因为有个y^2,很好理解。有时,曲线也可以是割裂开的,这里就不举例子了。椭圆曲线可以被看作把一个三次函数x轴以上的部分,变平一点,然后做一个镜像。这里可以参考原文,还有几张图描述了过程,很清晰。
在比特币中使用的椭圆曲线叫secp256k1,方程如下:
Coding Elliptic Curves in Python
我们对曲线本身其实并不感兴趣,感兴趣的是其上的点。比如,上面的曲线,我们感兴趣一个坐标(-1,1)。我们将定义class Point作为椭圆曲线上的一个点。
因为椭圆曲线有着标准形式:
所以,只用两个变量a和b就能定义曲线。
在第二章的代码ecc.py中,
- 可以check一个点是否在曲线上
- 两个点的坐标和曲线相等 ,才是两个相等的点
当我们创建Point对象时,如果点不在曲线上,也就是传入的x和y与a和b不符合,就会抛出异常。
参考examples.py。
Point Addition
椭圆曲线上的点的加法对我们很有用,两个曲线上的点相加得到第三个点,同样在曲线上。这被叫做加法是因为和普通的加法有相似之处,比如也是可交换的。A点+B点等于B点+A点。
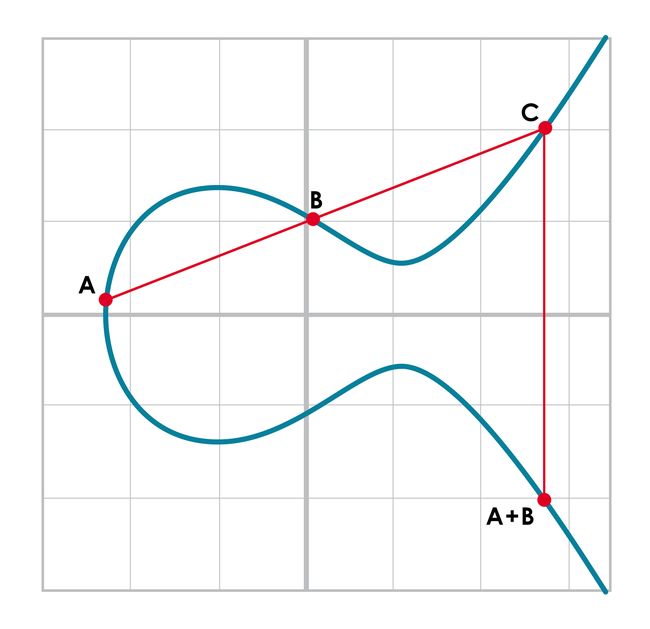
对于每个椭圆曲线来说,一条直线除了在是切线和垂直的情况下,要么和曲线有一个交点,要么有三个交点。我们把point addition定义为:
- 找到一条线穿过两个点之后的第三个点
- 对第三个点关于x轴reflect一下
图上可以说是很清晰了。我们可以用到这样特殊定义的加法的一个属性是,这样得到的点是不好预测的。我们可以用公式足够简单的计算Point addition,但是直觉上,给定两个点,第三个点可以出现在任何地方。比如A+B得到的是两个点右边的一个点,而A+C就会得到B的关于X轴的对称点,which在A和C之间,B+C会得到B和C左边的点。用数学术语来说,point addition是非线性的。
Math of Point Addition
point addition也满足普通加法的若干性质,比如:
- Identity 也就是存在一个点I + A = A(跟0一样)这个点我们叫做infinity (无穷远点,并不在椭圆曲线上)
- Commutativity 对于一个点A,存在-A 使得A + (-A) = I
- Associativity 可交换性 A + B = B + A
- Invertibility 可结合性 (A + B) + C = A + (B + C) (这里原文示意图很生动)
那么为了code我们的point addition,我们就要分三种情况:
- 两个点在垂直线上或者有点是infinity
- 两个点不在垂直线上,并且是不同的
- 两个点相同
Coding是很简单的,然后就是用公式推导出第三个点的坐标,可以参考原文,都是很简单的数学,大致就是先求出两个点的直线方程,再联合曲线方程求出第三个点的坐标。
注意有一个edge case,就是在两个点相同的情况下,如果两个点正好都是曲线最左端的点,也就是y坐标都为0,得到的切线是垂直的,那么返回无穷远点。
Conclusion
我们现在已经学习了椭圆曲线是什么,怎么做point addition。我们马上就要结合有限域和椭圆曲线来做ECC啦~
参考:
https://github.com/jimmysong/programmingbitcoin/blob/master/ch02.asciidoc