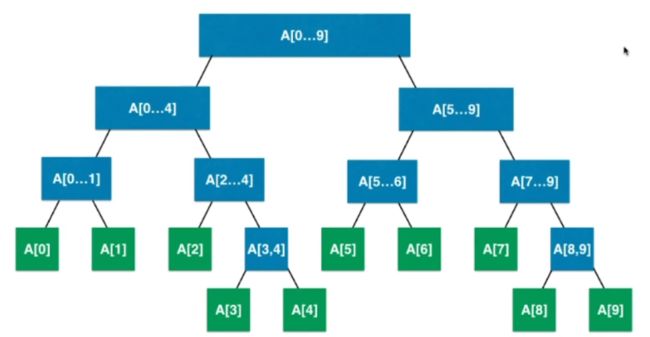
线段树用于处理区间数据的更新与查询问题,不考虑往区间中增加与删除数据的,主要用于统计数据方面的需求,在更新与查询的时间复杂度都为logn级别。线段树不属于完全二叉树,但属于平衡二叉树。
/**
*
* 功能描述:线段树
*
* @version 2.0.0
* @author zhiminchen
*/
public class SegmentTree {
// 用于存储线段数的数据
private E[] data;
// 用于存储原始数据
private E[] tree;
// 用于抽象线段树的统计操作
private Merger merger;
/**
*
* 功能描述:
*
* @version 2.0.0
* @author zhiminchen
*/
static interface Merger {
public E merge(E left,
E right);
}
/**
* 线段树的构造方法,传入的是一个数组与merger对象
* @param arr
* @param merger
*/
public SegmentTree(E[] arr, Merger merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
// 将arr传入的数据复制到data数组中
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
// 这里需要4倍的空间(tree是一个满二叉树的空间,需要考虑只有10个节点的情况)
tree = (E[]) new Object[arr.length * 4];
buildSegmentTree(0, 0, data.length - 1);
}
/**
*
* 功能描述: 在treeIndex的位置创建表示区间【left, right】的线段树
*
* @param treeIndex
* @param left
* @param right void
* @version 2.0.0
* @author zhiminchen
*/
private void buildSegmentTree(int treeIndex,
int left,
int right) {
// 递归终止条件
if (left == right) {
tree[treeIndex] = data[left];
return;
}
// treeIndex的左孩子节点的值
int leftIndex = getLeft(treeIndex);
// treeIndex的右孩子节点的值
int rightIndex = getRight(treeIndex);
// 找到线段树中间的区间,递归构造区间树的左右孩子节点
int mid = left + (right - left) / 2;
//
buildSegmentTree(leftIndex, left, mid);
buildSegmentTree(rightIndex, mid + 1, right);
// 这里贸给具体的业务逻辑处理
tree[treeIndex] = merger.merge(tree[leftIndex], tree[rightIndex]);
}
/**
*
* 功能描述:对线段树中的值进行更新
*
* @param index
* @param e void
* @version 2.0.0
* @author zhiminchen
*/
public void set(int index,
E e) {
if (index < 0 || index > data.length - 1) {
throw new IllegalArgumentException("index is illegal");
}
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
/**
*
* 功能描述: 在以treeIndex为根的线段树中 更新index的值为e
*
* @param treeIndex
* @param left
* @param right
* @param index
* @param E void
* @version 2.0.0
* @author zhiminchen
*/
private void set(int treeIndex,
int left,
int right,
int index,
E e) {
// 递归退出条件
if (left == right) {
tree[treeIndex] = e;
return;
}
int mid = left + (right - left) / 2;
// treeIndex的左孩子节点的值
int leftIndex = getLeft(treeIndex);
// treeIndex的右孩子节点的值
int rightIndex = getRight(treeIndex);
if (index >= mid + 1) { // 更新index在右子树的情况
set(rightIndex, mid + 1, right, index, e);
} else {
set(leftIndex, left, mid, index, e);
}
// 更新线段树的值
tree[treeIndex] = merger.merge(tree[leftIndex], tree[rightIndex]);
}
/**
*
* 功能描述: 查询某个区间的值
*
* @param queryLeft
* @param queryRight
* @return E
* @version 2.0.0
* @author zhiminchen
*/
public E query(int queryLeft,
int queryRight) {
return query(0, 0, data.length - 1, queryLeft, queryRight);
}
/**
*
* 功能描述: 在以treeIndex为根的线段树中区间为【left, right】, 搜索【queryLeft, queryRight】区间的值
*
* @param treeIndex
* @param left
* @param right
* @param queryLeft
* @param queryRight
* @return E
* @version 2.0.0
* @author zhiminchen
*/
private E query(int treeIndex,
int left,
int right,
int queryLeft,
int queryRight) {
// 如果搜索的区间正好是treeIndex的根节点,则直接返回
if (left == queryLeft && right == queryRight) {
return tree[treeIndex];
}
int mid = left + (right - left) / 2;
int leftTreeIndex = getLeft(treeIndex);
int rightTreeIndex = getRight(treeIndex);
// 区间的最小值比mid还大, 则在右子树进行查找。
if (queryLeft >= mid + 1) {
return query(rightTreeIndex, mid + 1, right, queryLeft, queryRight);
} else if (queryRight <= mid) { // 在线段树的左子树查找
return query(leftTreeIndex, left, mid, queryLeft, queryRight);
} else {
// 处理在左右子树都需要查找的情况
E leftResult = query(leftTreeIndex, left, mid, queryLeft, mid);
E rightResult = query(rightTreeIndex, mid + 1, right, mid + 1, queryRight);
return merger.merge(leftResult, rightResult);
}
}
public E get(int index) {
if (index < 0 || index >= data.length) {
throw new IllegalArgumentException("index is illegal");
}
return data[index];
}
/**
*
* 功能描述: (完全二叉树的数据表示)得到左孩子节点的索引
*
* @param index
* @return int
* @version 2.0.0
* @author zhiminchen
*/
public int getLeft(int index) {
return 2 * index + 1;
}
/**
*
* 功能描述:(完全二叉树的数据表示) 得到右孩子节点
*
* @param index
* @return int
* @version 2.0.0
* @author zhiminchen
*/
public int getRight(int index) {
return 2 * index + 2;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
for (int i = 0; i < tree.length; i++) {
if (tree[i] != null) {
sb.append(tree[i]);
} else {
sb.append("null");
}
if (i != tree.length - 1) {
sb.append(", ");
}
}
sb.append("]");
return sb.toString();
}
public static void main(String[] args) {
Integer[] data = new Integer[] {
1,
2,
3,
5,
-8,
9,
11,
2,
33,
45,
12
};
SegmentTree segTree = new SegmentTree(data, new Merger() {
public Integer merge(Integer left,
Integer right) {
return left + right;
}
});
System.out.println(segTree.query(1, 8));
segTree.set(5, 15);
System.out.println(segTree.query(1, 8));
}
}
/**
*
* 功能描述:采用树的方式实现线段树
*
* @version 2.0.0
* @author zhiminchen
*/
public class SegmentTree2 {
// 用于存储原始数据
private E[] data;
// 用于抽象线段树的统计操作
private Merger merger;
// 树的根结点
private Node root;
/**
*
* 功能描述: node结点,用于存储数据
*
* @version 2.0.0
* @author zhiminchen
*/
private static class Node {
E e;
int left; // 左区间起始位置
int right; // 右区间终止位置
Node leftNode;
Node rightNode;
Node(E e, int left, int right) {
this(e, left, right, null, null);
}
Node(E e, int left, int right, Node leftNode, Node rightNode) {
this.e = e;
this.left = left;
this.right = right;
this.leftNode = leftNode;
this.rightNode = rightNode;
}
}
public SegmentTree2(E[] arr, Merger merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
// 将arr传入的数据复制到data数组中
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
// 调用构造树的方法
root = buildSegmentTree(0, data.length - 1);
}
/**
*
* 功能描述: 构区间[left,right]的线段树
*
* @param left
* @param right
* @return Node
* @version 2.0.0
* @author zhiminchen
*/
private Node buildSegmentTree(int left,
int right) {
// 递归终止条件
if (left == right) {
return new Node(data[left], left, right);
}
// 找到线段树中间的区间,递归构造区间树的左右孩子节点
int mid = left + (right - left) / 2;
// 构建树的左结点
Node leftNode = buildSegmentTree(left, mid);
// 构建树的右结点
Node rightNode = buildSegmentTree(mid + 1, right);
// 求结点的值
E e = merger.merge(leftNode.e, rightNode.e);
// 返回结点
Node node = new Node(e, left, right, leftNode, rightNode);
return node;
}
/**
* 功能描述:对线段树中的值进行更新
*
* @param index
* @param e void
* @version 2.0.0
* @author zhiminchen
*/
public void set(int index,
E e) {
if (index < 0 || index > data.length - 1) {
throw new IllegalArgumentException("index is illegal");
}
data[index] = e;
set(root, 0, data.length - 1, index, e);
}
/**
*
* 功能描述: 在以treeIndex为根的线段树中 更新index的值为e
*
* @param left
* @param right
* @param index
* @param E void
* @version 2.0.0
* @author zhiminchen
*/
private void set(Node node,
int left,
int right,
int index,
E e) {
// 递归退出条件
if (left == right && node.left == left && node.right == right) {
node.e = e;
return;
}
int mid = left + (right - left) / 2;
if (index >= mid + 1) { // 更新index在右子树的情况
set(node.rightNode, mid + 1, right, index, e);
} else { //更新左子树的情况
set(node.leftNode, left, mid, index, e);
}
// 更新线段树的值
node.e = merger.merge(node.leftNode.e, node.rightNode.e);
}
/**
*
* 功能描述:查询【queryLeft, queryRight】区间的值
*
* @param queryLeft
* @param queryRight
* @return E
* @version 2.0.0
* @author zhiminchen
*/
public E query(int queryLeft,
int queryRight) {
return query(root, queryLeft, queryRight);
}
/**
*
* 功能描述: 在以treeIndex为根的线段树中区间为【left, right】, 搜索【queryLeft, queryRight】区间的值
*
* @param treeIndex
* @param left
* @param right
* @param queryLeft
* @param queryRight
* @return E
* @version 2.0.0
* @author zhiminchen
*/
private E query(Node node,
int queryLeft,
int queryRight) {
// 如果搜索的区间正好是treeIndex的根节点,则直接返回
if (node.left == queryLeft && node.right == queryRight) {
return node.e;
}
int mid = node.left + (node.right - node.left) / 2;
// 区间的最小值比mid还大, 则在右子树进行查找。
if (queryLeft >= mid + 1) {
return query(node.rightNode, queryLeft, queryRight);
} else if (queryRight <= mid) { // 在线段树的左子树查找
return query(node.leftNode, queryLeft, queryRight);
} else {
// 处理在左右子树都需要查找的情况
E leftResult = query(node.leftNode, queryLeft, mid);
E rightResult = query(node.rightNode, mid + 1, queryRight);
return merger.merge(leftResult, rightResult);
}
}
/**
*
* 功能描述:
*
* @version 2.0.0
* @author zhiminchen
*/
static interface Merger {
public E merge(E left,
E right);
}
public static void main(String[] args) {
Integer[] data = new Integer[] {
1,
2,
3,
5,
-8,
9,
11,
2,
33,
45,
12
};
SegmentTree2 segTree = new SegmentTree2(data, new Merger() {
// 用于求合统计
public Integer merge(Integer left,
Integer right) {
return left + right;
}
});
System.out.println(segTree.query(1, 8));
segTree.set(5, 15);
System.out.println(segTree.query(1, 8));
}
}