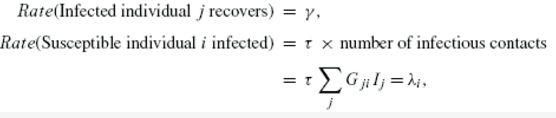致敬Keeling & Rohani,有这样无私的人世界才会更加进步!
我只是勤劳的翻译工和搬运工。
如图,主要介绍技术部分,自己留存,同时望指正。
| 符号 | 说明 |
|---|---|
| γ | 感染者的恢复率 |
| τ | 易感者的感染率 |
| Gij | 无向图,ij相连值为1,不相连值为0 |
| Ij | 当且仅当j是感染者,Ij值为1 |
| N | 规模大小,即有多少个节点 |
| n | 度,即每个人与他人相连数量的平均值 |
| Type | 代码中写了四个,随机、网格、小世界、空间 |
function [t,S,I] = Program_7_7(N,n,tau,gamma,MaxTime,Type)
% Program_7_7( N, n, tau, gamma, MaxTime, Type)
% This is the MATLAB version of program 7.7 from page 280 of
% "Modeling Infectious Disease in humans and animals"
% by Keeling & Rohani.
%
% It is an SIS disease spread through a network. Allowed
% network types are 'Random','Spatial','Lattice' and 'SmallWorld'
%
% We assume N individuals, each with an averge of n contacts.
% In this model we define an individual by their status flag:
% Status=1 => Susceptible
% Status=2 => Infectious
% Status=0 => Recovered
% Sets up default parameters if necessary.
if nargin == 0
N=100;
n=4;
tau=1;
gamma=0.1;
MaxTime=1000;
Type='Random';
end
% Checks all the parameters are valid
CheckGreater(N,0,'Number of individuals N');
CheckGreater(n,0,'Number of neighbours n');
CheckGreater(tau,0,'tau');
CheckGreater(gamma,0,'gamma');
CheckGreater(MaxTime,0,'MaxTime');
%Initialise the Network
% (X,Y) is location, G is the network graph matrix
% this means we use S and I for the number of susceptibles and infecteds
[X,Y,G,N]=Create_Network(N,n,Type);
Status=1+0*X; Status(1)=2;
Rate=0*X; Rate(1)=gamma; Rate(find(G(:,1)))=tau;
t=0; i=1; S=N-1; I=1;
% The main iteration
subplot(2,1,1);
[j,k,s]=find(G);
plot([X(j) X(k)]',[Y(j) Y(k)]','-k');
hold on
Col=[0.7 0.7 0.7; 0 1 0; 1 0 0];
for k=1:N
H(k)=plot(X(k),Y(k),'ok','MarkerFaceColor','g');
end
set(H(1),'MarkerFaceColor','r');
hold off;
drawnow;
while (t0)
[step,Rate,Status,e]=Iterate(Rate,Status,G,tau,gamma);
i=i+1;
t(i)=t(i-1)+step;
S(i)=length(find(Status==1));
I(i)=length(find(Status==2));
set(H(e),'MarkerFaceColor',Col(Status(e)+1,:));
% subplot(2,1,1);
% [j,k,s]=find(G);
% plot([X(j) X(k)]',[Y(j) Y(k)]','-k');
% hold on
% s=find(Status==0); plot(X(s),Y(s),'ok','MarkerFaceColor',[0.7 0.7 0.7],'MarkerSize',8);
% s=find(Status==1); plot(X(s),Y(s),'ok','MarkerFaceColor','g','MarkerSize',8);
% s=find(Status==2); plot(X(s),Y(s),'ok','MarkerFaceColor','r','MarkerSize',10);
% hold off;
subplot(4,1,3);
plot(t,S,'-g');
ylabel 'Number of Susceptibles'
subplot(4,1,4);
plot(t,I,'-r');
ylabel 'Number of Infecteds'
xlabel 'Time'
drawnow;
[];
end
% Create the Network
function [X,Y,G,N]=Create_Network(N,n,Type);
if n > (N-1)
error('Impossible to have an average of %d contacts with a population size of %d',n,N);
end
G=sparse(1,1,0,N,N);
X=rand(N,1); Y=rand(N,1);
switch Type
case {'Random','random'}
contacts=0;
while(contactsrand(1,1)*Sum));
Status(Event)=mod(Status(Event)+1,3);
contacts=find(G(:,Event) & Status==1);
switch Status(Event)
case 1
case 2
Rate(Event)=gamma;
Rate(contacts)=Rate(contacts)+tau;
G(Event,:)=0;
case 0
% For SIR type dynamics we require the following 2 lines
Rate(Event)=0;
Rate(contacts)=Rate(contacts)-tau;
% For SIS type dynamics we require the following 3 lines
%Status(Event)=1;
%Rate(Event)=tau*length(find(G(:,Event) & Status==2));
%Rate(contacts)=Rate(contacts)-tau;
end
Rate=Rate.*sign(Status);
step=-log(rand(1,1))/Sum;
% Does a simple check on the value
function []=CheckGreaterOrEqual(Parameter, Value, str)
m=find(Parameter0
error('Parameter %s(%g) (=%g) is less than %g',str,m(1),Parameter(m(1)),Value);
end
function []=CheckGreater(Parameter, Value, str)
m=find(Parameter<=Value);
if length(m)>0
error('Parameter %s(%g) (=%g) is less than %g',str,m(1),Parameter(m(1)),Value);
end