原作者 :张江
作者简介:北京师范大学系统科学学院副教授张江
原发平台:混沌巡洋舰 微信二维码
微信号 :chaoscruiser
简 介:一门新兴学科,正悄悄重塑我们对世界的理解。经济,政治,物理,心理,看似不相关,却被一个叫复杂科学的学科深层相连。我们将带你从它的视角,看世界的全景。
原文链接:戳这里
本文作者 北京师范大学系统科学学院副教授张江,授权转载。
流动是复杂系统中的普遍现象之一,从看得见的流动,例如:水流、人流;到看不见的流动,如:电流、能量流、热流;再到更加抽象的:货币流、信息流等等,似乎如果一个系统是复杂的,它的内部就一定存在着各种流动。那么是否存在着某个普遍的规律制约着这些流动呢?答案应该是肯定的,虽然这种规律仍然“犹抱琵琶半遮面”,但是近年来有关生态学、非平衡态统计物理的研究已经逐渐逼近它,各种迹象表明,一种统一的可以描述复杂系统中“流动”现象的通用规律即将“横空出世”。我们为什么会衰老和死亡?大象为什么比蟑螂吃得多而繁殖得少?少数大公司为什么能垄断市场?城市的交通网络为什么与动物体内的血管那么相似?也许这些问题最终都能在这套新理论中找到答案。本文的目的就是想引领读者赶上复杂性研究前沿的步伐,亲身体验这些激动人心的科学发现。
本篇文章分为三章: 一、流动与幂律 二、分形输运网络 三、通向理论,将分三天连载。
一、流动与幂律
1、流量与存量
假设你是一个公司的老板,正在运营一家拥有M亿元固定资产的企业,那么,你要保证每个月净盈利多少亿F才能使你的企业能够维持下去?很显然,这个问题取决于你这个公司每个月烧多少钱。由于每个月你都需要给你的员工开工资、需要交房租、需要购买新的电脑,那么这些花费的总和一定是一个与M有关的量。一般来说,M越大,公司每个月的花费F也越大,你需要为更多的人开工资、需要维护更昂贵的计算机设备,因此每个月公司需要赚取的净盈利也就越大。那么F和M究竟存不存在着某种数量关系呢?
不要着急回答这个问题,让我们先来看看大自然。大自然有各种各样的物种,每个物种都有着不同的重量(body mass)。同时每个物种都需要新陈代谢,它们需要不停的从外界环境获取能量资源以维持自身的生命。如果设一个物种的平均重量是M,它的新陈代谢量是F,那么一般来说M越大F也越大。大象要维持生存一天总要比老鼠吃的多得多。
对比这两个问题,我们会发现它们有着下面的类比关系:
公司 <-> 物种
固定资产 <-> 平均重量
每月的净盈利 <-> 新陈代谢
货币 <-> 能量
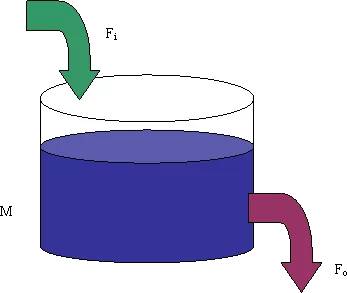
广义上说,这样的问题属于一种流量和存量的问题。由于公司的月盈利以及生物的新陈代谢都是一种流量,而固定资产和生物的重量都是一种存量。公司或者生物需要进行广义的新陈代谢从外界获取资源而转化成内部的存量。我们可以形象地用下图表示这个关系:
物种和公司就好比是这个大水缸,只不过一个存的是钱,另一个存的是能量。由于这个存量M会由于热力学第二定律(无序度持续增加)而不断地衰退,也就是说这个水缸是漏的,每时刻都有一个流出Fo,例如公司要计算各种固定资产的折旧费、生物则会因为新陈代谢而不断消耗着能量,因此,它需要不断补给流入Fi以维持M。当Fi=Fo的时候,系统的流入和流出平衡了,M就是不变的了。我们称这种状态为稳衡态(steady state),即一种动态之中的平衡。
不难想象,这里讨论的类似流、存储等概念并没有限定为具体的能量流或者货币流,因此,这是一种广义的流的问题,它普遍存在于各种复杂系统之中。你不妨自己寻找一下这个隐喻在城市系统、计算机系统、互联网、经济系统等系统中的应用。
2、神奇的数字3/4
下面,我们来具体探讨存量M究竟和流量F是一种什么关系。最早发现M与F之间存在着明确关系的是在生物界。1932年,一个叫Max Kleiber的生物学家对各种鸟类、哺乳类动物的尺寸M与新陈代谢F之间的关系进行了测量,并将它们的对数值画到一张图中,发现所有的数据点都排列到了一条直线上,如图:
这说明,F与M之间的确存在着一种幂律关系也就是F=F0Mb,其中F0和b都是常数。经测量发现,这个直线的斜率b接近于3/4这个数。这个关系后来又被Brody证实,小到老鼠,大到大象,新陈代谢和生物体重量之间的关系都符合确定的关系式:F=F0M3/4。
其中,F0是一个与M无关的常数。随后,Hemmingsen又将这个结论扩展到了更多的物种,小到单细胞生物大到白鲸,它们的新陈代谢和生物量的关系都服从幂律分布:F~M3/4。
(这个符号的意思是指F和M3/4成比例。虽然对于不同的物种集合来说F0有可能不同,但是指数3/4却都是一样的)
因为对于生物来说,它的体积(Body Size)是与重量呈正比的,所以,这个关系也表达了新陈代谢和体积V的关系:F~V3/4。
仔细分析这个公式发现,它符合我们的直觉,即越大的生物体需要更大量的能量来维持自己的新陈代谢。一头大象显然要比一只老鼠吃得多。其次,这个公式也有反直觉的一方面。一般我们人普遍认为F与M是呈一种正比的关系即F~M。这样,当生物体体积增长10000倍的时候,它的新陈代谢也同样增长10000倍。然而,根据F~M3/4,事实却是当生物体增长10000倍,它的新陈代谢却仅仅增长1000倍,要小于线性增长的关系。因此,生物体为了维持每单位体积所需要的新陈代谢的能量是F/M~M-1/4,反而会随着体积的增大而减小。因此,大象比老鼠能够更有效率利用吸收来的能量,即越大越好,所以3/4律蕴含了一种“规模效益”。
3、异速生长尺度规律(Allometric scaling)
当我们有了3/4律,还可以得到更多有意思的推论。因为我们可以把生物体理解为一个盛水的水缸,新陈代谢作为一种流动不断更新这个水缸里面的水。那么,我们考虑一单位新陈代谢吸收的能量会在水缸中平均逗留多长时间而被排出?经过很简单的计算可以得出,这个时间大概是:T=M/F~M/M3/4=M1/4,即与重量呈1/4的幂律关系。
经过试验验证人们发现,生物体的各种时间量,例如寿命、发育时间、怀孕时间都与它的重量的1/4呈正比。因为时间的倒数就是频率,因此,不难推论生物的各种频率(即快慢程度),如:心跳频率、出生率、死亡率(出生率与死亡率是针对整个种群而言的)都与M呈-1/4的幂律关系,即:Q~M-1/4。这里面的Q是生物的任何一种“频率”。
这也就是说个头越大的生物,它的一切活动就会显得越慢,个头越小的则一切活动都越快。这很符合我们的经验观察:小老鼠喜欢不停的跳来跳去的,而大象则移动身躯都很费劲。(参考James Brown的文献)
生物体的寿命与重量呈1/4的幂律关系有些出人意料,这意味着实际上任何生物在诞生之日起已经被该物种的平均重量决定了其寿命。然而,该理论并没有指出生物为什么会衰老、为什么会死亡?也许对这一问题的解答现在还不是时候,不过从流动的角度来看,可以肯定的是衰老和死亡一定是跟生物体的新陈代谢有关系的。为了进一步阐明衰老、死亡和流动、新陈代谢的关系,作者作了这样一个有关流水的比喻。
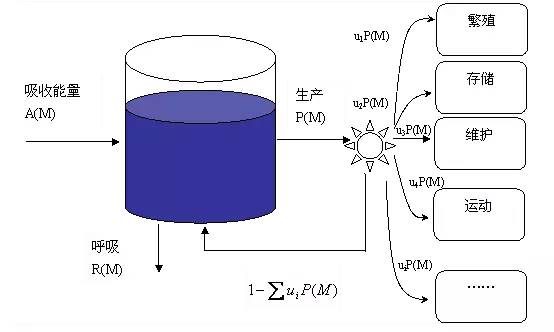
上面的水缸比喻实际是一个生物体能量利用的简化版本,生物体吸收能量之后不仅仅能维持生存,而且还能进行运动、捕食、生育后代、学习文化知识,这些活动都需要消耗能量,因而,水缸之中的水流动就会得到一幅更复杂的生物体内能量流图,详细请看这里:
这幅图表示的含义是:生物体从环境吸收到一定的能量作为总的能量输入,其中有相当一部分是通过呼吸作用燃烧能量转化成废热而排出体外。还有一部分能量则因为生产活动而创造出一些对生物体自身有意义的做功输出,例如繁殖、存储(转化成一些储备能量的生物物质,如脂肪)、维护(替换掉身体中的一些坏掉的部件)、运动(捕食活动等)……。由于生物的生产能量不见得都能转化成有用功,因此还有相当一部分能量又重新回流到了生物体内。我们知道,任何一种消耗能量的活动都不能做到百分之百的能量利用效率,因此都会产生废热,所有活动的废热都由呼吸作用由体表排出体外了。
值得注意的是,这些流量都与生物体的重量(尺寸)呈3/4幂律关系,也就是说F~M3/4中的F是生物体内的一种能量的利用。所以生物体进行生产的能量P~M3/4,这部分能量会被生物分成不同的比例作为各种用途使用。因此比例u1、u2...ui针对不同的生物体来说是不同的,它们反应为生物体为了适应环境而演化出来的不同投资策略。例如有的生物专门投资到繁殖这部分,那么这种生物就表现出非常强的繁殖能力(如蟑螂)。而有的则专门投资到运动部分,那么它就表现出非常快的奔跑速度(如猎豹)。但是,所有这些投资都不能任意的增长,它们都会有一个上限,这个上限主要是由它的重量(或体积)决定的。所以,猎豹再进化也不可能进化出接近光速的奔跑速度来。
需要指出的是,这里面提到的各种幂律关系都是针对不同物种求平均值得到的统计数据而言的。因而,它不一定适用于同一个物种中的不同个体。因此,我们并不能得出结论,根据寿命和体积的幂律关系T~M1/4,越胖的人寿命越长。对于不同人来说,自然寿命可能由各种因素决定,但是对于整个人类来说,寿命数值和体积数值是固定的,这两者服从一种幂律关系。
所有这些生物体的幂律关系有个统一的名称叫做:异速生长尺度律(Allometric scaling)。这里的Scaling就是指的各种生物量与生物体的体积大小有关,它们会随着生物体尺度的变化而变化。而异速生长则是指这种关系不是与尺度呈正比,即增长多少体积就会增长多少新陈代谢,而是呈现各种幂律关系,也就是说它们的增长速度是不同的。
4、无处不在的流动与幂律
本文开篇就指出,流动是一种普遍存在的现象,那么3/4幂律分布关系是否也能推广到各种复杂系统之中呢?答案是半对半错。3/4这个特定的数字可能不再成立,然而幂律关系是普遍存在的,下面我们来看几个具体的例子。
我们可以把城市比喻成一个生命系统,它也需要不断的从外界吸收各种物质、能量资源,也会像现实生物一样成长、发育、衰老。从这个角度看,给城市供给的各种能量、物质资源就相当于是输入到城市中的流或城市的新陈代谢,而消费这些能量、物质的人就可以看作是这个城市的存量,或者尺寸。城市越大,它能供养的人越多,因而需要的能量和物质也就越多。
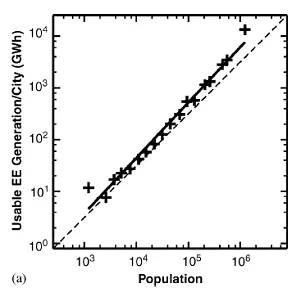
德国的Christian Kuhnert等人就将德国各个城市的人口数(相当于M)和供给该城市的总电能(即F)进行了统计,并把这两个量的对数值画在一张图上得到了近似直线的分布曲线:
发现这条直线的斜率近似1.1,即F~M1.1。另外,他还统计了欧洲各个国家不同城市的人口数量与加油站数量、邮局的数量、饭馆的数量等量(这些量都可以看作是广义的流量F)之间的关系,发现类似的幂律分布曲线也可以得到,并且幂律指数一般都接近于1。这个例子说明,流量与存量这对关系在一切复杂系统中都有着相似的数量关系。(参考Kuhnert的文献)
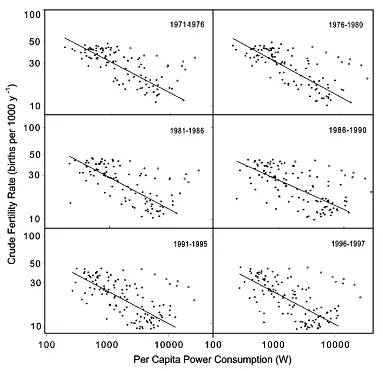
为什么越穷的国家或地区越愿意生孩子?而越富有的国家则生育率极低?生物学家Melaine Moses 对美国在不同时期的平均每人消耗的资源和这一年的生育数量的对数值画到曲线上,得到了下图:
其中对于整个国家来说人均资源消耗就相当于是新陈代谢率F。在前面讨论的各种幂律关系中,有一个关系是出生率与生物体尺度的关系:Q~M-1/4,同时我们知道F~M3/4,这样不难得到:Q~F-1/3,这也就是上图统计出来的对数图中的直线表示的。看来,在强大的新陈代谢流动的自然规律面前,我们人类并没有多大的选择权利。(参考Moses的文献)
让我们回到一开始的公司规模问题。是否公司的资产规模也和公司的盈利存在着类似的这种幂律分布关系,甚至是不是这个分布的指数就是3/4呢?就笔者目前掌握的资料来看,没有人做过这个统计。但是,关于公司尺寸的分布存在着一个相关的幂律分布,这就是公司的规模与这种规模的公司数量之间存在着幂律分布关系:N~M-b,其中b是一个正数。也就是说公司规模越大,相应的数量越小。这个关系已经被很多社会学家证明了,并且在社会学中,这个规律有个特定的名字叫做Zipf律。它也许可以间接证明存量与流量的幂律关系。(参考Axtell的文献)
如果将经济系统中的公司与生态系统中的生物体之间的类比是正确的,那么,我们有理由相信由能量流驱动构造的生物与由货币流驱动构造的公司遵循着同样的规律。这样不仅仅流量和存量之间服从着幂律分布关系,而且其他的有关时间尺度、频率与存量之间的幂律关系也可能试用。像生物一样,小公司好比是老鼠,相对灵活多变,但是平均寿命也短;而大公司就好比是大象,体积庞大、反应缓慢,但实力雄厚,存在的寿命也长。
让我们放眼大千世界,这样的流量与存量、时间与规模之间的矛盾和关系几乎到处存在,所以最初来源于生物学的3/4律的发现也许蕴藏着一切复杂系统共有的规律。
“流”的探索(二)——分形输运网络
“流”的探索(三)——通向理论
本文版权归混沌巡洋舰所有,如需转载请联系混沌巡洋舰,禁止不获取授权的任何形式的转载,包括且不限于纸媒、微博、微信、公众号。
微信号 :chaoscruiser
简 介:一门新兴学科,正悄悄重塑我们对世界的理解。经济,政治,物理,心理,看似不相关,却被一个叫复杂科学的学科深层相连。我们将带你从它的视角,看世界的全景。
原文链接:戳这里